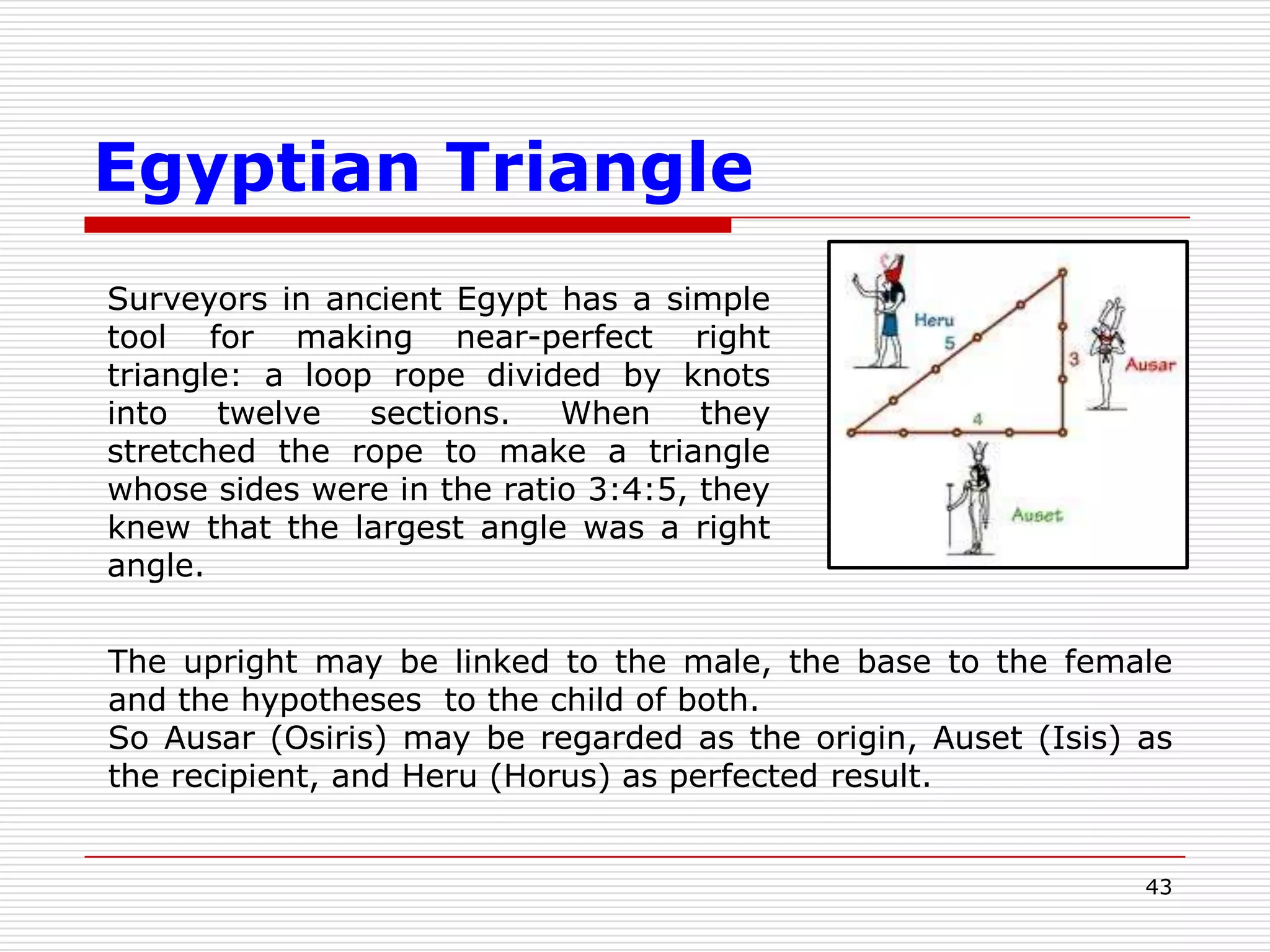
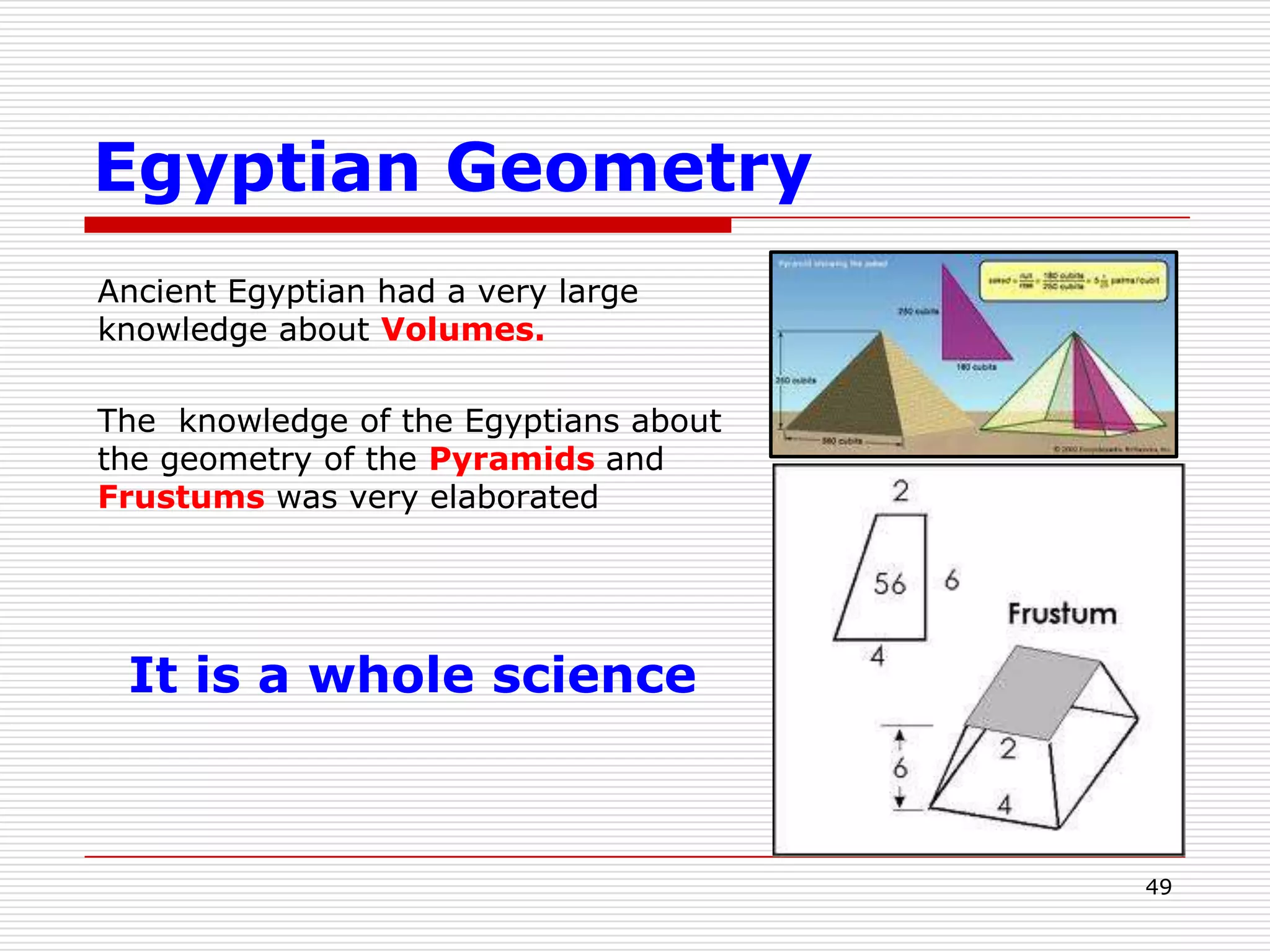
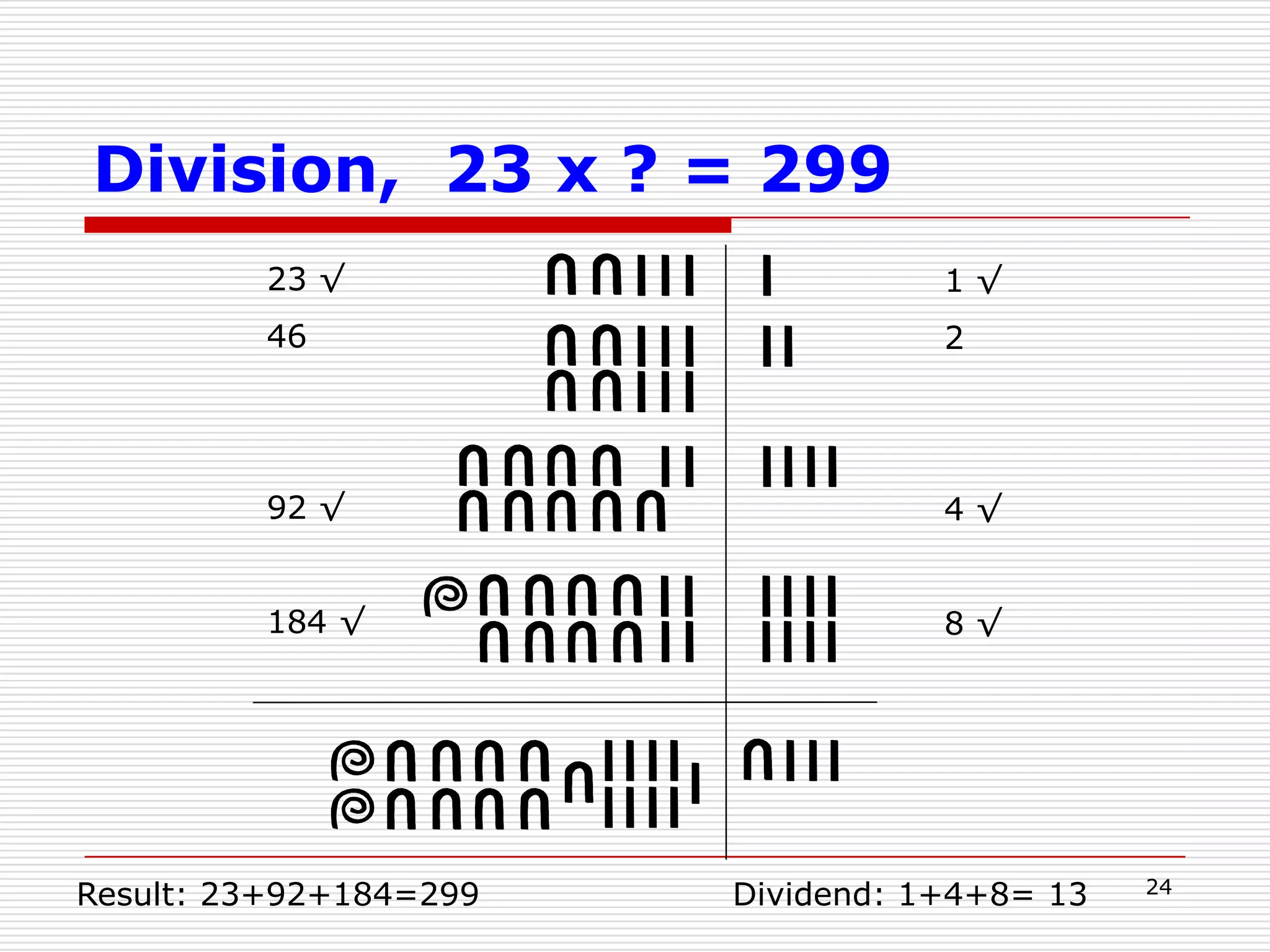
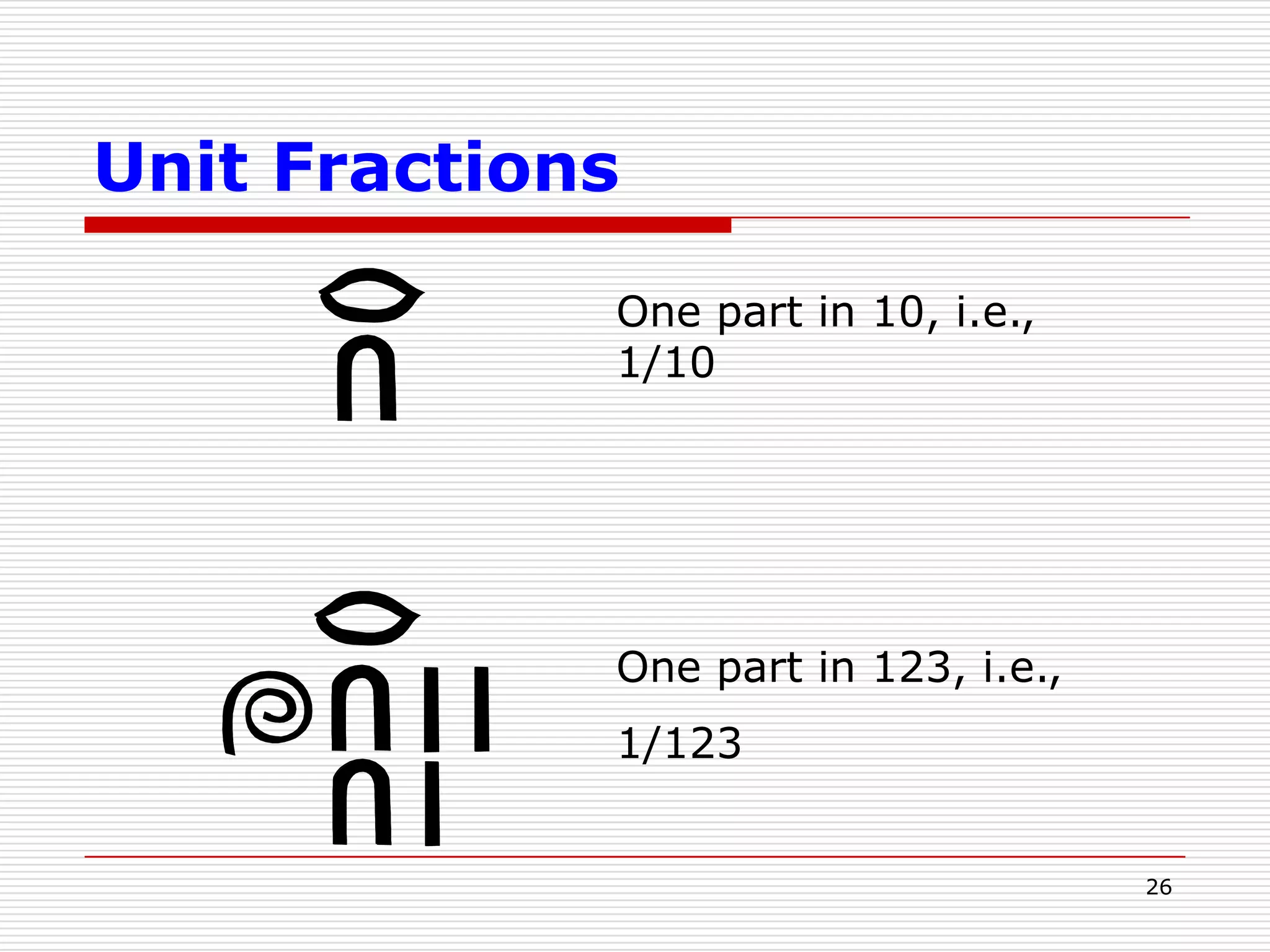
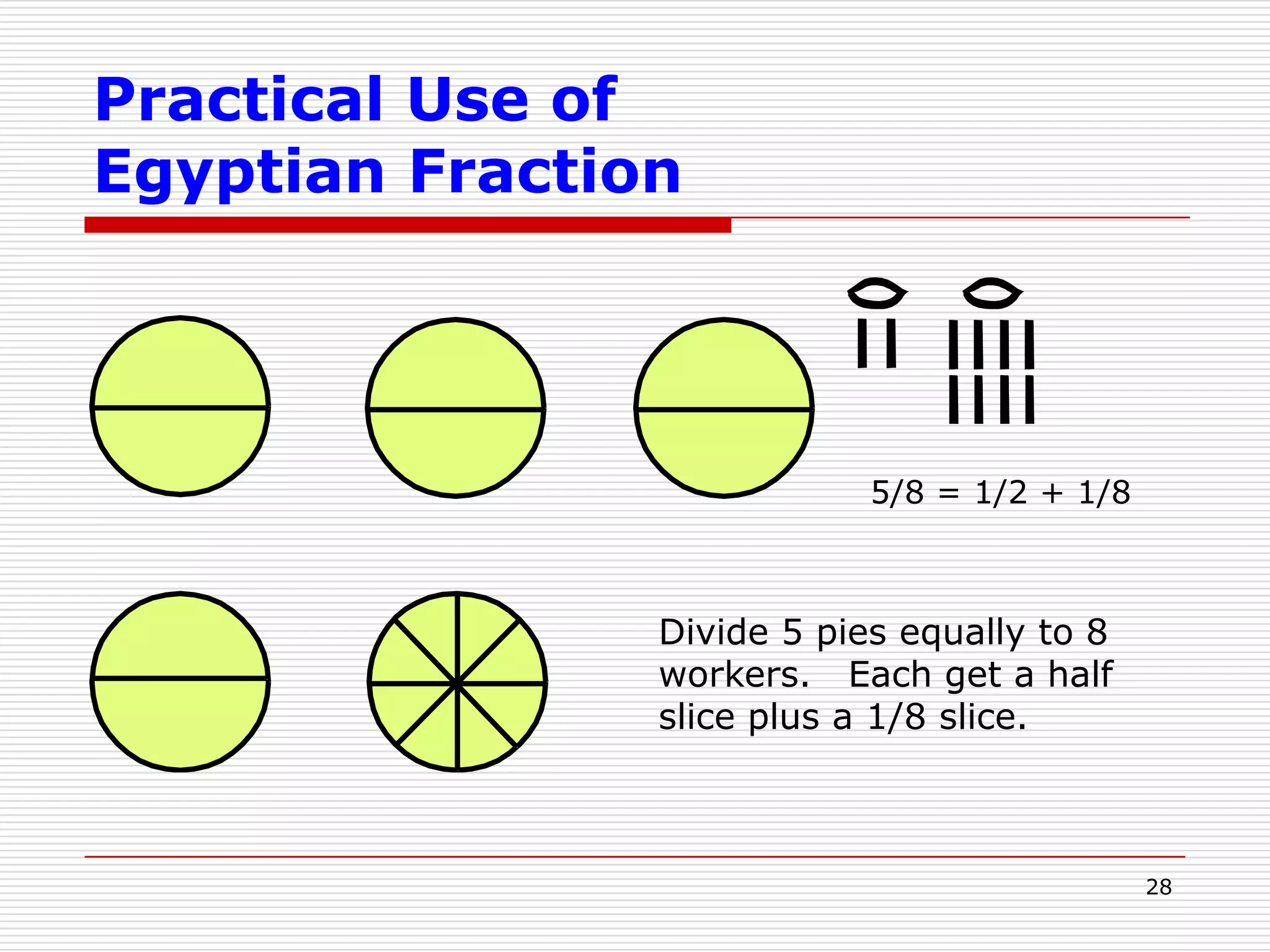
This document provides an overview of ancient Egyptian mathematics and its timeline. It discusses the Egyptian numeral system, which was additive, as well as their arithmetic operations of addition, multiplication and division. The Egyptians were able to solve linear equations and used arithmetic and geometric progressions. They could also express fractions as a sum of unit fractions. Overall, the document demonstrates the Egyptians had sophisticated mathematical knowledge and methods as early as 3000 BC.

1. 1EGYPTOLOGYEGYPTIANMATHEMATICSMOKHTAR ELNOMROSSY

2. 2EgyptologyEgyptianMathematicsTimeline of Ancient Egyptian Civilization

3. Egyptian Numerals

4. Egyptian Arithmetic

5. Egyptian Algebra

6. Egyptian Geometry3EgyptianMathematicsTimelineofAncient EgyptianCivilization

7. 4Early Human

8. 5Timeline ofAncient Egyptian CivilizationPrehistoric EraLower Paleolithic Age 200000 – 90000 B.C.Middle Paleolithic Age 90000 – 30000 B.C.Late Paleolithic Age 30000 - 7000 B.C.Neolithic Age 7000 - 4800 B.C.

9. 6EgyptEgyptian civilization begins more than 6000 years ago, with the largest pyramids built around 2600 B.C.

10. 7Timeline ofAncient Egyptian CivilizationPredynastic PeriodUpper EgyptBadarian Culture 4800 – 4200 B.C.Amratian Culture (Al Amrah) 4200 – 3700 B.C.Gersean Cultures A & B (Al Girza) 3700 – 3150 B.C.* 365 day Calendar by 4200 B.C.*From 3100 B.C exhibited numbers in millionsLower EgyptFayum A Culture (Hawara) 4800 – 4250 B.C.Merimda Culture 4500 – 3500 B.C. (Merimda Bani Salamah)

11. 8Egyptian CalendarAs early as 4241 B.C, the Egyptians had created a calendar made up of twelve months of 30 days, plus five extra days at the end of the year.The Egyptian Calendar, dated 4241 B.C, is based on the solar year and daily revolution of the earth around the sun.Evidently, to reach this feat in calculating the days the earth takes to move round the sun in one year, Egyptian by then must have possessed knowledge of astronomy and mathematics

12. 9Timeline ofAncient Egyptian CivilizationDynastic PeriodEarly dynastic period 3150 – 2685 B.C. (Dynasties 1 & 2)Old Kingdom 2685 – 2160 B.C. (Dynasties 3 to 8)In about 2600 B.C, the Great Pyramid at Giza is constructedFirst Intermediate Period 2160 – 2040 B.C. (Dynasties 9 to 11)Middle Kingdom 1991 – 1668 B.C. (Dynasties 12 & 13)1850 BC “Moscow Papyrus” contains 25 mathematical problems

13. 10Pyramid from Space

14. 11Timeline ofAncient Egyptian CivilizationDynastic PeriodSecond Intermediate Period 1668 - 1570 B.C. (Dynasties 14 to 17)1650 BC “Ahmes Papyrus’ contains 85 mathematical problemsNew Kingdom 1570 - 1070 B.C. (Dynasties 18 to 20)Late Period 1070 - 712 B.C. (Dynasties 21 to 24)Dynasty 25 (Kushite domination) 712 – 671 B.C. Assyrian DominationSaite Period (Dynasty 26) 671 - 525 B.C. Dynasties 27 to 31 525 – 332 B.C Persian Period

15. 12Ahmes Papyrus (Rhind)Part of the Rhind papyrus written in hieratic script about 1650 B.C. It is currently in the British Museum. It started with a premise of “a thorough study of all things, insight into all that exists, knowledge of all obscure secrets.” It turns out that the script contains method of multiply and divide, including handling of fractions, together with 85 problems and their solutions.

16. 13Egyptian MathematicsEgyptian Numerals

17. 14Rosetta Stone & Egyptian LanguageThe stone of Rosette is a basalt slab (114x72x28cm) that was found in 1799 in the Egyptian village of Rosette (Rashid).Today the stone is kept at the British Museum in London.It contains three inscriptions that represent a single text in three different variants of script, a decree of the priests of Memphis in honor of Ptolemalos V (196 BC).The text appears in form of hieroglyphs (script of the official and religious texts), of Demotic (everyday Egyptian script), and in Greek.The representation of a single text of the three script variants enabled the French scholar Jean Francois Champollion in 1822 to basically to decipher the hieroglyphs. Furthermore, with the aid of the Coptic language, he succeeded to realize the phonetic value of the hieroglyphs. This proved the fact that hieroglyphs do not have only symbolic meaning, but that they also served as a “spoken language”.

18. 15Egyptian HieroglyphsThis is the hieroglyphic inscription above the Great pyramid’s entrance.Egyptian written language evolved in three stages:HieroglyphsHieraticCoptic (spoken only)

19. 16Egyptian NumbersThe knob of King Narmer, 3000BCThe numerals occupy the center of the lower register. Four tadpoles below the ox, each meaning 100,000 record 400,000 oxen. The sky-lifting-god behind the goat was the hieroglyph for “one million”; together with the four tadpoles and the two “10,000” fingers below the goat, and the double “1,000” lotus-stalk below the god, this makes 1,422,000 goats.To the right of these animal quantities, one tadpole and two fingers below the captive with his arms tied behind his back count 120,000 prisoners.These quantities makes Narmer’s mace the earliest surviving document with numbers from Egypt, and the earliest surviving document with such large numbers from anywhere on the planet.

20. 17Egyptian NumeralsEgyptian number system is additive.

21. 18Egyptian MathematicsEgyptian Arithmetic

22. 19Addition in Egyptian Numerals 365+ 257= 622

23. 20Multiply 23 х 13multiplicand23 √4692 √184 √1 √24 √8 √1 + 4 + 8 = 1323+92+184 = 299multiplier 13Result:

24. 21Principles of Egyptian MultiplicationStarting with a doubling of numbers from one, 1, 2, 4, 8, 16, 32, 64, 128, etc.Any integer can be written uniquely as a sum of “doubling numbers”.Appearing at most one time.11 = 1 + 2 + 8 23 = 1 + 2 + 4 + 16 44 = 4 + 8 + 32

25. 22Binary ExpansionAny integer N can be written as a sum of powers of 2.Start with the largest 2k ≤ N, subtract of it, and repeat the process. 147 = 128 + 19 ; 19 = 16 + 3 ; 3 = 2 +1 So 147 = 128 + 16 + 2 + 1 with k = 7, 4, 1, 0

26. 23Principles of Egyptian MultiplicationApply distribution law:a x (b + c) = (a x b) + (a x c)Example:

27. 23 x 13 = 23 x (1 + 4 + 8) = 23 + 92 + 184 = 299

28. 24Division, 23 х ? = 29923 √4692 √184 √1 √24 √8 √Result: 23+92+184=299Dividend: 1+4+8= 13

29. 25Numbers that cannot divide evenly e.g.: 35 divide by 88 1 16 2√ 32 4 4 1/2 √ 2 1/4√ 1 1/8 35 4 + 1/4 + 1/8doublinghalf

30. 26Unit FractionsOne part in 10, i.e., 1/10One part in 123, i.e.,1/123

31. 27Egyptian Fractions1/2 + 1/4 = 3/41/2 + 1/8 = 5/81/3 + 1/18 = 7/18The Egyptians have no notations for general rational numbers like n/m, and insisted that fractions be written as a sum of non-repeating unit fractions (1/m). Instead of writing ¾ as ¼ three times, they will decompose it as sum of ½ and ¼.

32. 28Practical Use of Egyptian Fraction5/8 = 1/2 + 1/8Divide 5 pies equally to 8 workers. Each get a half slice plus a 1/8 slice.

33. 29Algorithm for Egyptian FractionRepeated use of

34. Example:30Egyptian MathematicsEgyptian Algebra

35. 31Arithmetic ProgressionProblems 40 & 64 of RMP.Now we follow the scribe’s directions word by word, but we substitute for the numbers he used those letters commonly used in modern algebraic treatment of arithmetic progression, thus: a = first term (lowest) l = last term (highest) d = common difference n = number of terms S = sum of n termsThe scribe direct:Find the average value of the n terms = S/n

36. The number of differences is one less than the number of terms = (n-1)

37. Find half of the common difference = d/232Arithmetic ProgressionProblems 40 & 64 of RMP.Multiply that (n-1) by d/2 = (n-1)d/2

38. Then either add this to the averaged = S/n + (n-1)d/2, this is the highest term l, then, l = S/n + (n-1)d/2 or it can be written as S/n = l – (n-1)d/2, hence, S = n/2[2l – (n-1)d]Or subtract this from the averaged value = S/n – (n-1)d/2, this is the lowest term a, then, a = S/n – (n-1)d/2 or it can be written as S/n = a + (n-1)d/2, hence, S = n/2[2a + (n-1)d]

39. 33Geometric ProgressionProblems 76 & 79 of RMPBecause of the Egyptian method of performing all multiplications by continued doubling, it was natural enough that they should be interested in numbers arranged serially, and especially the series1, 2, 4, 8, 16, ….This series is called a geometric progression whose first term is 1 and whose common multiplier is 2

40. It has a special property, which the Egyptians were aware of and which is today made use of in the design of modern digital computers

41. This property is that every integer can be uniquely expressed as the sum of certain terms of the series. Thus, an integral multiplier, when partitioned in this form, can be used in Egyptian multiplication.34Geometric ProgressionProblems 76 & 79 of RMPThe importance of this property to the Egyptian scribes lies in the uniqueness of the partitioning of any multiplier.

42. For example: The multiplier 26 can be expressed as the sum of terms of this in one way only, namely, 2+8+16Thus, it is understandable that the Egyptian’s attention would quite naturally be directed to the sum of certain terms of this and other series, and that those properties of progressions that could be used in subsequent calculations would interest them deeply.35Geometric ProgressionProblems 76 & 79 of RMPTherefore, let us look at the property of GP described in RMP 76, namely,2, 4, 8, 16, 32, 64, …. The sum of the first 2 terms is 6 = 2x(1+ 1st term) = 6 The sum of the first 3 terms is 14 = 2x(1+1st 2 terms) = 14 The sum of the first 4 terms is 30 = 2x(1+1st 3 terms) = 30 The sum of the first 5 terms is 62 = 2x(1+1st 4 terms) = 62 The sum of the first 6 terms is 126= 2x(1+1st 5 terms) = 126Then, by inductive reasoning the Egyptian scribe have concluded that, in any GP, whose common multiplier is the same as the first term, the sum of any number of its terms is equal to the common ratio times one more than the sum of the preceding terms.36Equations of first degreeProblems 24 to 34 of the RMPThe eleven problems deal with the methods of solving equations in one unknown of the first degree.

43. Based upon the order of difficulty and method of solution, these problems fall into three groups.

44. The first group:Pr 24: A quantity and its 1/7 added becomes 19.What is the quantity?Pr 25: A quantity and its ½ added becomes 16. What is the quantity? Pr 26: A quantity and its ¼ added becomes 15. What is the quantity? Pr 27: A quantity and its 1/5 added becomes 21. What is the quantity?

45. 37Equations of first degreeProblems 24 to 34 of the RMPEach of these problems is solved by the method known as “false position’, and each deals with abstract numbers unrelated to loaves bread, hekats of grains, or the area of fields.

46. The scribe is showing with four similar problems, but different numbers, a general method of solution for this type of problems.

47. The number “falsely assumed” in each case is the simplest that could be chosen, namely, 7, 2, 4, 5 respectively.

48. Problem 24; Assume the false answer 7. then, 1 1/7 of 7 is 8. Then as many times as 8 must be multiplied to give 19, just so many times 7 be multiplied to give the correct number.

49. 38Equations of first degreeProblems 24 to 34 of the RMP 1 8 \2 \16 ---------------------------------------- 1/2 4 \1/4 \2 \1/8 \1 ----------------------------------------Total 2 1/4 1/8 19 Now, multiply 2 1/4 1/8 by 7 \1 \2 1/4 1/8 \2 \4 1/2 1/4 \4 \9 1/2 ------------------------------------------------ Total 7 15 (1/2 1/2) (1/4 1/4) 1/8 7 16 1/2 1/8 The answer, then, is 16 1/2 1/8

50. 39Equations of first degreeProblems 24 to 34 of the RMPSecond group:Two problems constitute the second group. They are:Problem 28: A quantity and its 1/3 added together, and from the sum a third of the sum is subtracted and 10 remains. What is the quantity?Problem 29: A quantity and its 1/3 are added together, 1/3 of this added, then 1/3 of this sum is taken, and the result is 10. What is the quantity?Both of these problems are discussed under “think of a number”

51. 40Equations of first degreeProblems 24 to 34 of the RMPThird group:The third group consists of problems 30 – 34Problem 30: If the scribe says, “What is the quantity of which (1/3 1/10) will make 10”.Problem 31: A quantity, its 1/3; its 1/2 and its 1/7 added becomes 33. What is the quantity?Problem 32: A quantity, its 1/3 and its ¼ added to become 2. What is the quantity?Problem 33: A quantity, its 1/3; its 1/2 and its 1/7 added becomes 37. What is the quantity?Problem 34: A quantity, its 1/2 and its 1/4 added becomes 10. What is the quantity?The scribe solved these problem by a different method,That of division

52. 41Equations of second degreeSimultaneous equationsTwo problems in the Berlin Papyrus appear to deal clearly with the solution of simultaneous equations, one being of the second degree.The scribe proposed to solve the following two sets of equations:Set 1: x2 + y2 = 100 4x – 3y = 0Set 2: x2 + y2 = 400 4x – 3y = 0

53. 42Egyptian MathematicsEgyptian Geometry

54. 43Egyptian TriangleSurveyors in ancient Egypt has a simple tool for making near-perfect right triangle: a loop rope divided by knots into twelve sections. When they stretched the rope to make a triangle whose sides were in the ratio 3:4:5, they knew that the largest angle was a right angle.The upright may be linked to the male, the base to the female and the hypotheses to the child of both. So Ausar (Osiris) may be regarded as the origin, Auset (Isis) as the recipient, and Heru (Horus) as perfected result.

55. 44Area of RectangleThe scribes found the areas of rectangles by multiplying length and breadth as we do today.Problem: 49 of RMPThe area of a rectangle of length 10 khet (1000 cubits) and breadth 1 khet (100 cubits) is to be found 1000x100= 100,000 square cubits.The area was given by the scribe as 1000 cubits strips, which are rectangles of land, 1 khet by 1 cubit.

56. 45Area of RectangleProblem: 6 of MMPCalculation of the area of a rectangle is used in a problem of simultaneous equations.The following text accompanied the drawn rectangle.Method of calculating area of rectangle.If it is said to thee, a rectangle in 12 in the area is 1/2 1/4 of the length.For the breadth. Calculate 1/2 1/4 until you get 1. Result 1 1/3Reckon with these 12, 1 1/3 times. Result 16Calculate thou its angle (square root). Result 4 for the length.1/2 1/4 is 3 for the breadth.

57. 46Area of RectangleProblem: 6 of MMP(In modern form)A = L x bL x b = 12 and b = (1/2 1/4)L Then, inverse of 1/2 1/4 is 1 1/3L x L = 12 x 1 1/3 = 16Therefore, L = 4 for the lengthAnd 1/2 1/4 of 4 is the breadth 3.

58. 47Area of triangleFor the area of a triangle, ancient Egyptian used the equivalent of the formula A = 1/2bh.Problem: 51 of RMPThe scribe shows how to find the area of a triangle of land of side 10 khet and of base 4 khet.The scribe took the half of 4, then multiplied 10 by 2 obtaining the area as 20 setats of land.Problem: 4 of MMPThe same problem was stated as finding the area of a triangle of height (meret) 10 and base (teper) 4.No units such as khets or setats were mentioned.

59. 48Area of CircleComputing πArchimedes of Syracuse (250BC) was known as the first person to calculate π to some accuracy; however, the Egyptians already knew Archimedes value of π = 256/81 = 3 + 1/9 + 1/27 + 1/81Problem: 50 of RMPA circular field has diameter 9 khet. What is its area?The written solution says, subtract 1/9 of the diameter which leaves 8 khet. The area is 8 multiplied by 8 or 64 khet. This will lead us to the value of π = 256/81 = 3 + 1/9 + 1/27 + 1/81 = 3.1605But the suggestion that the Egyptian used is π = 3 = 1/13 + 1/17 + 1/160 = 3.1415

60. 49Egyptian GeometryAncient Egyptian had a very large knowledge about Volumes.The knowledge of the Egyptians about the geometry of the Pyramids and Frustums was very elaboratedIt is a whole science

61. 50Egyptian MathematicsThank You