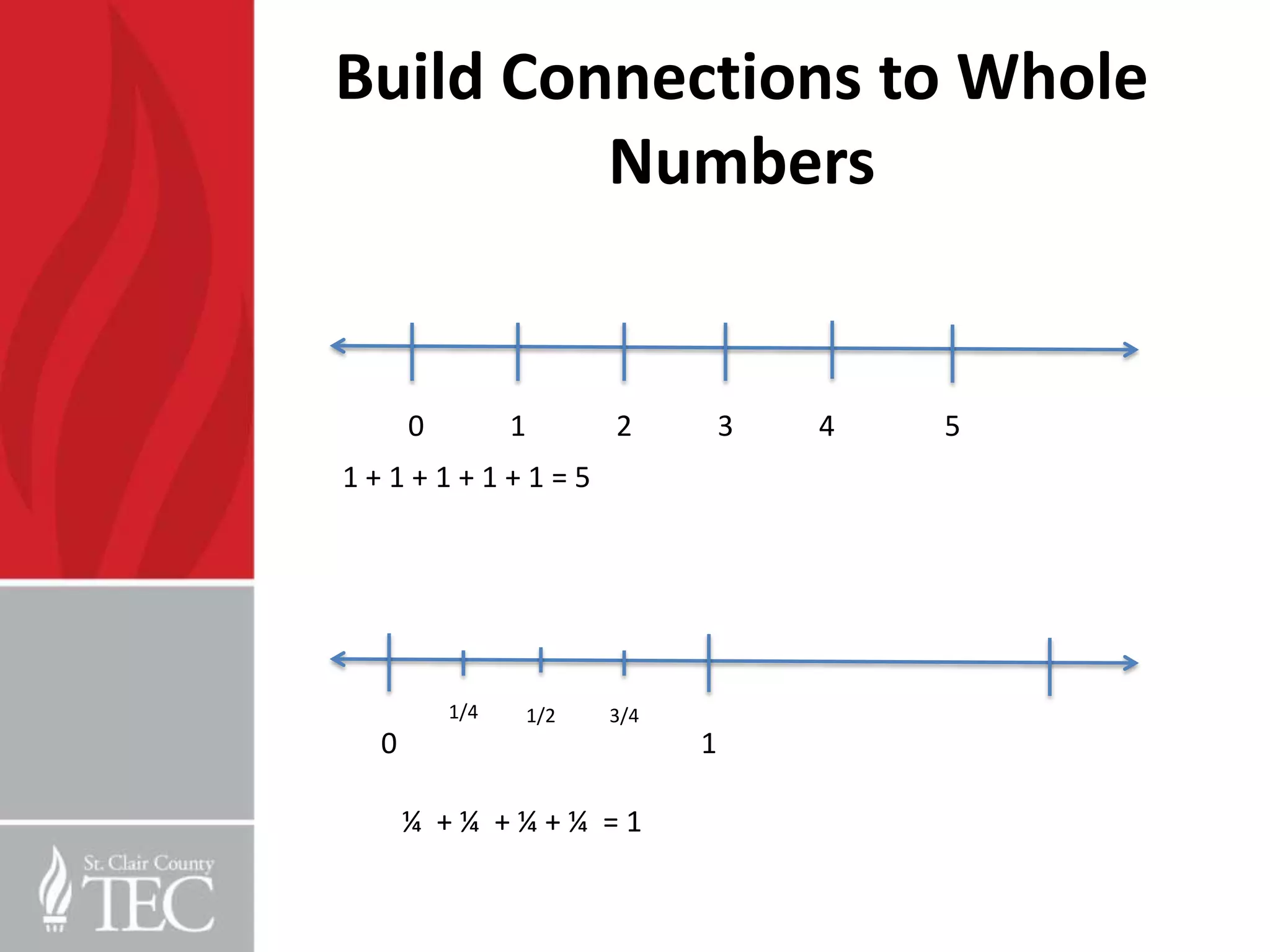
This document provides information and resources for teaching fractions and word problems to 5th grade students. It includes the common core standards for fractions, learning targets, example word problems, and strategies for using bar diagrams and number lines. It also discusses key fraction concepts like equivalent fractions, addition and subtraction of fractions, and multiplication and division of fractions. Resources are provided like video links, articles, and websites to support teaching fractions.

1. 5th
Grade
Fractions &
Word Problems
Laura Chambless
RESA Consultant
www.protopage.com/lchambless

2. CCSS and Gaps
What are your gaps in curriculum?
1. Review CCSS for Fractions
2. Think about your resources
3. Think about your teaching
– Highlight anything your resources
covers well in YELLOW.
– Highlight any part of the standard you
would like more clarification on in
BLUE.

3. Learning Target
Use equivalent fractions as a strategy to
add and subtract fractions.
5.NF.1, 5.NF.2
Apply and extend previous understandings
of multiplication and division to multiply
and divide fractions.
5.NF.3, 5.NF.4, 5.NF.5, 5.NF.6, 5.NF.7

4. Fraction Word Problem
40 students joined the soccer club.
5/8 of the students were boys.
How many girls joined the soccer
club?
Draw a picture and solve it.
1. 2 min. working problem on own
2. 5 min. sharing with group
3. Class discussion
Found at: http://www.mathplayground.com/wpdatabase/Fractions1_3.htm

5. Problem Solving with
Bar Diagrams
1. Understand: Identify what is known and what is
unknown. Draw the bar diagram to promote
comprehension and demonstrates
understanding. (Situation vs. Solution Equation)
2. Plan: Decide how you will solve the problem
(find the unknown). Analyze the bar diagram to
find a solution plan.
3. Solve: Execute the plan. Use the bar diagram to
solve.
4. Evaluate: Assess reasonableness using
estimation or substitution. Substitute the
solution for the unknown in the bar diagram.

6. Bar Diagrams
Watch Introduction Video
http://www.mhschool.com/math/com
mon/pd_video/mathconnects_bardi
agram_p1/index.html
http://www.mhschool.com/math/com
mon/pd_video/mathconnects_bardi
agram_p2/index.html

7. Practice Bar Diagrams
To: Rani earned $128 mowing lawns and $73
babysitting. How much money did Rani earn?
With: Jin had $67 in his pocket after he bought a
radio controlled car. He went to the store with
$142. How Much did Jin spend on the car?
By: There are 9 puffy stickers. There are 3 times
as many plain stickers as puffy stickers. How
many plain stickers are there?
You pick 2 more to do by yourself. Share with
partner
Draw Your Way to Problem Solving Success Handout, Robyn Silbey

8. Thinking Blocks
http://www.mathplayground.com/think
ingblocks.html
Explore the site 
When done exploring go to my
Protopage and look at your grade
level math tab.

9. Fractions
Stand and Share
Make a list of what you know and any
connections you have about the
fraction ¼.

10. Build Connections to Whole
Numbers
0 1 2 3 4 5
1+1+1+1+1=5
1/4 1/2 3/4
0 1
¼ +¼ +¼+¼ =1

11. Fractions
Fraction Activity
Paper Strips Fraction Kit:
1, ½, 1/4 , 1/8, 1/16
Add to Fraction Kit: 1/3, 1/6, 1/12
Add to Fraction Kit: 1/5, 1/10
Compare/Add/Subtract/Multi./Divide with Strips
READ and DO:
5.NF.1, 5.NF.2, 5.NF.3, 5.NF.4, 5.NF.5, 5.NF.6, 5.NF
.7
Smaller Answer Wins (need dice)
• Prove with Fraction Strips

12. Lunch

13. Definition of Fractions
1. Make a list of what you would like
to have in a definition of a fraction
2. Partner up and compare lists
3. Group discussion

14. Definition of a Fraction
Create a working definition of a fraction
– Watch Dev-TEAM video 3:5 and 3:6
– Give article: Definitions and Defining in
Mathematics and Mathematics Teaching
by: Bass and Ball

15. Definition Of Fractions
• Identify the whole
• Make d equal parts
• Write 1/d to show one of the equal
parts
• If you have d of 1/d, then you have the
whole
• If you have n of 1/d, then you have n/d
• n and d are whole numbers
• d does not equal 0
Dev-TE@M • School of Education • University of Michigan • (734)
408-4461 • dev-team@umich.edu For review only - Please do not
circulate or cite without permission

16. Ordering Fractions
Order Fractions
8/6, 2/5, 8/10, 1/12
How did you figure out what order
they went in?

17. Fractions
Prove with Fraction Strips
Number Line: (Benchmarks) 0, ½, 1
Equivalent Fractions: Same Name Frame
Compare (>/<): same numerator or same
denominator

18. Strategies for Comparing
Fractions
• Dev-TE@M session 9

19. Fraction On A Number Line
Writing about Fractions:
Draw a number line.
Place 3/6 and 7/12 on the number line.
Compare the two fractions- why did put
them where you did?

20. Conventions Of A Number Line
Dev-TE@M • School of Education • University of Michigan • (734) 408-4461 •
dev-team@umich.edu For review only - Please do not circulate or cite without
permission

21. Model of Number Line Talk
• Watch Dev-TE@M Session 4:5 (video)

22. Talking Through A Number Line
1. Understand the problem.
2. Think about which representation you
are going to use.
3. Describe your thinking process while
constructing the number line.
4. Sum up the solution that proved your
answer.
Model Example: 3/10 & 6/8

23. Fraction On A Number Line
Using a number line, compare 5/6 and
3/8 and tell which one is greater .
Have a partner listen to you as you
construct the fractions and find the
answer.

24. Fractions
What conceptual understanding do students need?
1. Begin with simple contextual tasks.
2. Connect the meaning of fraction computation with
whole number computation.
3. Let estimation and informal methods play a big role in
the development of strategies.
4. Explore each of the operations using models.
Van De Walle Book: Number Sense and Fraction
Algorithms Pg. 310

25. Equivalence with Fraction
Strips
• Fraction Strips
½+¼= ¾ + 1/3 =

26. Methods for Generating and
Explaining Equivalent Fractions
• Dev-TE@M session 9

27. Add/Subtract Fractions with
Unlike Denominators
Developing Equivalent Fractions
• Slicing Squares
Van de Walle book: pg. 304-305
3 x = 3 x
4 =
4
3 x 3 x =
= 4
4

28. Add/Subtract Fractions with
Unlike Denominators
Developing Equivalent Fractions
• Missing-Number Equivalencies
Van de Walle book: pg. 304-305
5 2 6
= =
3 6 3

29. Fraction Multiplication
Strategies
TOOLKIT for Multiplication of Fractions
1. Skim over TOOLKIT
2. Read assigned page (2 min)
3. 30 second report: What are the
important part of your page?
4. Questions from audience

30. Fractions
Multiply a fraction by a whole number
• Work as a group
• Use Fraction strips to show answers
4 x 1/3
¼ x 12
• What connection can you make to
multiplication? What other
representations can you use? Can
you use a number line?

31. Multiple a Fraction by a Whole
Number
4 x 1/3 (4 groups of 1/3) = 4/3 = 1 1/3
I want 4 ribbons each at 1/3 of a yard. How much
ribbon will I need to purchase?
1/3 2/3 3/3 4/3
¼ x 12 (1/4 of 12) = 3
I have 12 cookies and want each of my friends
to have ¼ of them. How many cookies will
each friend get?

32. Scaling (resizing)
• 5.NF.5
– Read learning targets and discuss
– Prove greater/less than given number
statements with last slide.
– Making equivalent fractions

33. Multiply Fraction by Fraction
AIMS
• Fair Squares and Cross Products
MMPI
• Worksheet 1: Show different
representations
2/3 of ¾ ¾ of 2/3

34. Multiply Fractions and Mixed
Numbers
MMPI
• Area Model
Rectangular Multiplication PPT
http://www.michiganmathematics.org/

35. Fraction as Division
(a/b = a ÷ b)
• I can explain that fractions (a/b) can be
represented as a division of the numerator
by the denominator (a ÷ b) can be
represented by the fraction a/b.
• I can solve word problems involving the
division of whole numbers and interpret the
quotient- which could be a whole number,
mixed number, or fraction – in the context of
the problem.
• I can explain or illustrate my solution
strategy using visual fraction models or
equations that represent the problem.

36. Divide Fraction by Whole
Number
½÷6=
6÷¼=
4 ÷ 2 = (how to connect division of
whole numbers with fractions)

37. Divide Fraction by Whole
Number
½ ÷ 6 = If I have ½ cup of sugar and
divide it among 6 people, how much
sugar does each person have? 1/12
1 2 3 4 5 6 7 8 9 10 11 12
6 ÷ ¼ = If I have 6 candy bars and divide
each one into fourths, how many
pieces will I have? 24

38. MOPLS
http://mi.learnport.org
Search: MOPLS Math
(navigate by using top tabs)
Look at Concepts Tab
– Introduction
– Math Behind the Math
– Misconceptions
– Tasks & Strategies

39. Fractions Online
Check out some sites on my 5th
grade math Protopage

40. Learning Target
Use equivalent fractions as a strategy to
add and subtract fractions.
5.NF.1, 5.NF.2
Apply and extend previous understandings
of multiplication and division to multiply
and divide fractions.
5.NF.3, 5.NF.4, 5.NF.5, 5.NF.6, 5.NF.7

41. Closer Activity
List something you learn about story
problems and fractions today.

42. Thanks for a great day 
Please contact me if you have any questions or
would like more information.