Danbi Cho, profile picture
Uploaded byDanbi Cho
PDF, PPTX80 views

Decision tree and ensemble

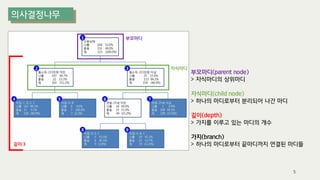
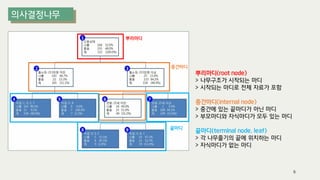
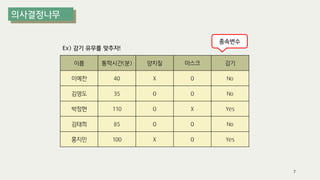
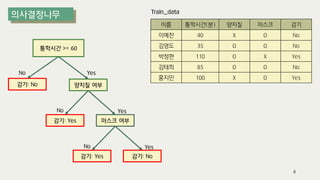
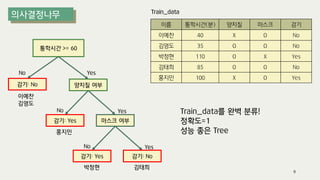
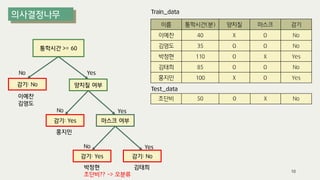
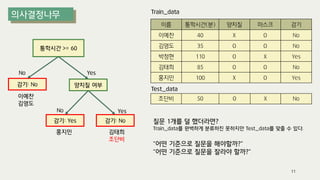
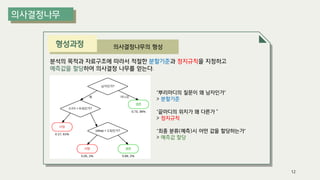
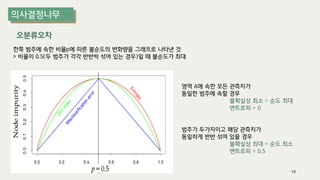
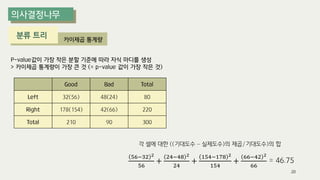
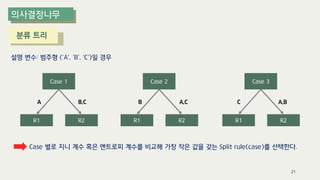
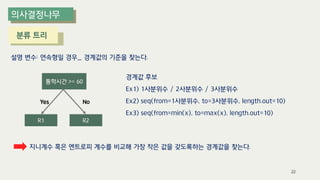
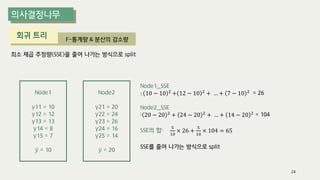
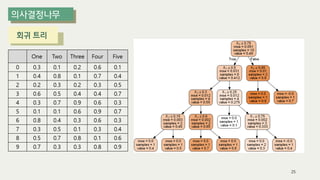
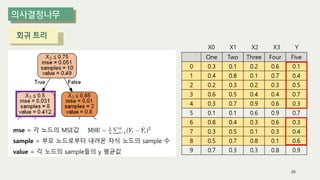
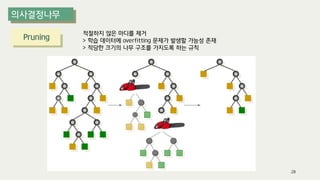
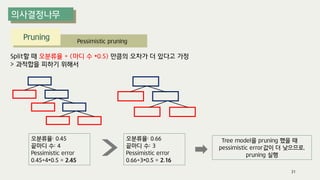
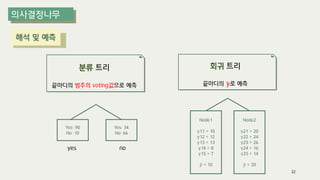
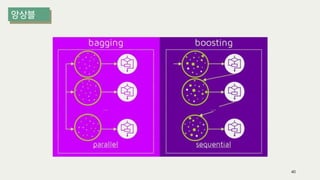
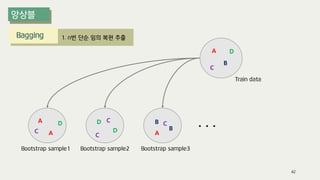
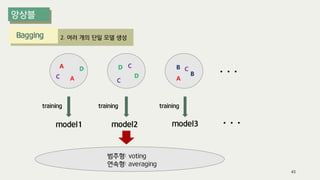
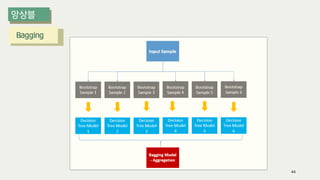
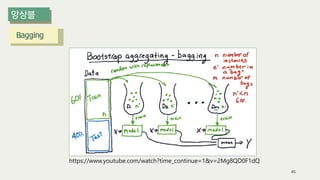
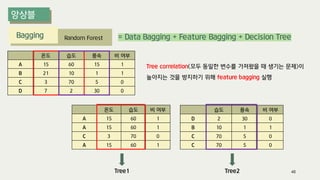
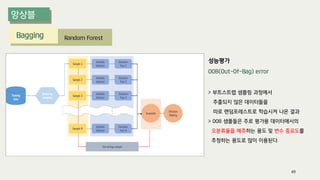
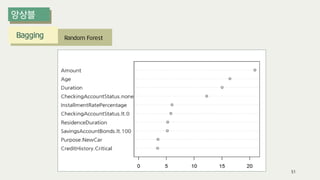
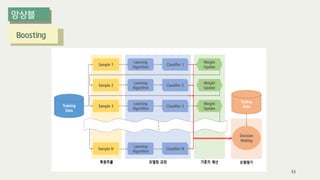
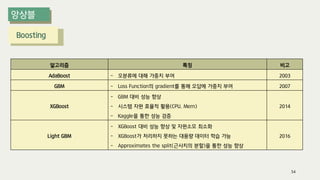
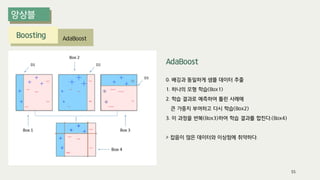
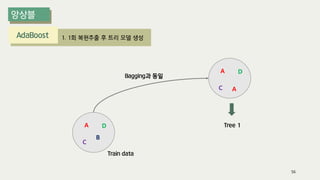
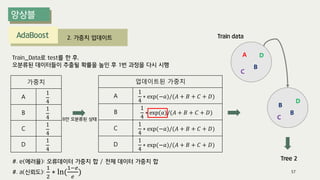
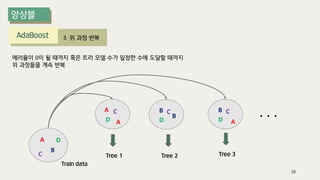
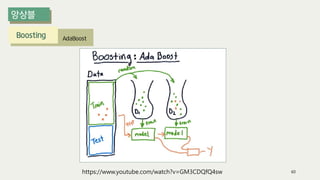
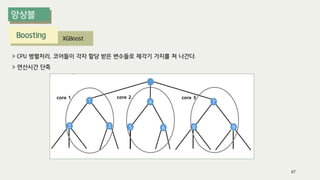
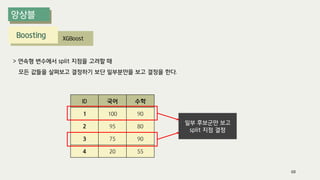
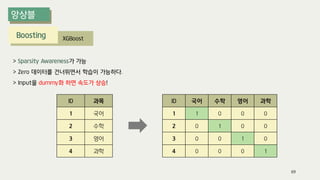
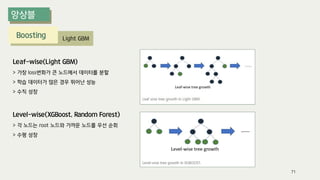
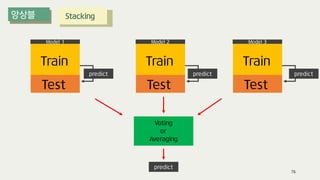
The document outlines the process of decision tree formation and application in classification and prediction tasks. It discusses the methodologies used for segmentation, classification, prediction, and interaction effect identification, along with the structure and components of decision trees such as nodes, branches, and depth. Additionally, it addresses the importance of rules for splitting, stopping, and pruning trees to avoid overfitting, and emphasizes the need for ensemble methods to improve predictive power.

Embed presentation

Download as PDF, PPTX
BOAZ 11기 조단비
01 02 03 배깅 부스팅 스태킹 01 02 03 모델 형성과정 정리
Decision Tree 분류 / 예측을 하는 지도학습 방법론 의사결정 규칙(Decision Rule)에 따라서 Tree를 생성한 후에 분류 / 예측하는 방법론 3
목적 1). 세분화(Segmentation) 데이터를 비슷한 특성을 갖는 몇 개의 그룹으로 분할, 그룹별 특성을 발견하는 경우 또는 각 데이터가 어떤 집단에 속하는지를 파악하고자 하는 경우 Ex) 시장 세분화, 고객 세분화 2). 분류(Classification) 관측개체를 여러 예측변수들에 근거해 목표변수의 범주를 몇 개의 등급으로 분류하고자 하는 경우 Ex) 고객을 신용도에 따라 우량/불량으로 분류 3). 예측(Prediction) 자료에서 규칙을 찾아내고 이를 이용해 미래의 사건을 예측하고자 하는 경우 Ex) 고객속성에 따라 대출한도액을 예측 4). 차원축소 및 변수선택(Data reduction and variable screening) 매우 많은 수의 예측변수 중에서 목표변수에 큰 영향을 미치는 변수들을 골라내고자 하는 경우 5). 교호작용효과의 파악(Interaction effect identification) 여러 개의 예측변수들을 결합해 목표변수에 작용하는 규칙(교호작용효과)을 파악하고자 하는 경우 6). 범주의 병합 또는 연속형 변수의 이산화(Binning) 범주형 목표변수의 범주를 소수의 몇 개로 병합하거나 연속형 목표변수를 몇 개의 등급으로 이산화 하고자 하는 경우 4
부모마디(parent node) > 자식마디의 상위마디 자식마디(child node) > 하나의 마디로부터 분리되어 나간 마디 깊이(depth) > 가지를 이루고 있는 마디의 개수 가지(branch) > 하나의 마디로부터 끝마디까지 연결된 마디들 부모마디 자식마디 깊이:3 5
뿌리마디 중간마디 끝마디 뿌리마디(root node) > 나무구조가 시작되는 마디 > 시작되는 마디로 전체 자료가 포함 중간마디(internal node) > 중간에 있는 끝마디가 아닌 마디 > 부모마디와 자식마디가 모두 있는 마디 끝마디(terminal node, leaf) > 각 나무줄기의 끝에 위치하는 마디 > 자식마디가 없는 마디 6
이름 통학시간(분) 양치질 마스크 감기 이예찬 40 X O No 김영도 35 O O No 박정현 110 O X Yes 김태희 85 O O No 홍지민 100 X O Yes 종속변수 Ex) 감기 유무를 맞추자! 7
8 Train_data 이름 통학시간(분) 양치질 마스크 감기 이예찬 40 X O No 김영도 35 O O No 박정현 110 O X Yes 김태희 85 O O No 홍지민 100 X O Yes 통학시간 >= 60 양치질 여부 감기: No 감기: Yes 마스크 여부 No Yes No Yes 감기: Yes 감기: No No Yes
Train_data를 완벽 분류! 정확도=1 성능 좋은 Tree 9 Train_data 이예찬 김영도 홍지민 박정현 김태희 이름 통학시간(분) 양치질 마스크 감기 이예찬 40 X O No 김영도 35 O O No 박정현 110 O X Yes 김태희 85 O O No 홍지민 100 X O Yes 통학시간 >= 60 양치질 여부 감기: No 감기: Yes 마스크 여부 No Yes No Yes 감기: Yes 감기: No No Yes
10 Train_data 이예찬 김영도 홍지민 박정현 김태희 조단비 50 O X No Test_data 이름 통학시간(분) 양치질 마스크 감기 이예찬 40 X O No 김영도 35 O O No 박정현 110 O X Yes 김태희 85 O O No 홍지민 100 X O Yes 통학시간 >= 60 양치질 여부 감기: No 감기: Yes 마스크 여부 No Yes No Yes 감기: Yes 감기: No No Yes 조단비?? -> 오분류
11 Train_data 이예찬 김영도 홍지민 조단비 50 O X No Test_data 이름 통학시간(분) 양치질 마스크 감기 이예찬 40 X O No 김영도 35 O O No 박정현 110 O X Yes 김태희 85 O O No 홍지민 100 X O Yes 통학시간 >= 60 양치질 여부 감기: No 감기: Yes 감기: No No Yes No Yes 김태희 조단비 질문 1개를 덜 했더라면? Train_data를 완벽하게 분류하진 못하지만 Test_data를 맞출 수 있다. “어떤 기준으로 질문을 해야할까?” “어떤 기준으로 질문을 잘라야 할까?”
분석의 목적과 자료구조에 따라서 적절한 분할기준과 정지규칙을 지정하고 예측값을 할당하여 의사결정 나무를 얻는다. 의사결정나무의 형성 “뿌리마디의 질문이 왜 남자인가” > 분할기준 “끝마디의 위치가 왜 다른가＂ > 정지규칙 “최종 분류(예측)시 어떤 값을 할당하는가“ > 예측값 할당 12 형성과정
Split Rule(Growing Rule): Tree의 분리 규칙/ 성장 규칙 - 부모 마디로부터 자식 마디를 생성하는 기준 - 순수도: 목표변수의 특정 범주에 개체들이 포함되어 있는 정도 - 목표 변수 구별 정도를 순수도 or 불순도에 의해서 측정 - 순수도가 증가할수록 분할기준에 따라 자식마디 형성 Stop Rule: 정지 규칙 - 분리가 더 이상 일어나지 않도록 하는 기준 Pruning: 가지치기 - Tree가 지나치게 많은 마디를 가지고 있을 경우, overfitting의 문제 발생 - 부적절한 마디를 잘라내 모형을 단순화 13 의사결정나무의 형성 형성과정
타당성 평가 이익도표(Gain chart)나 위험도표(Risk chart) 또는 Cross validation을 이용해서 tree 평가 해석 및 예측 생성한 Tree에 새로운 데이터 대입 후, 분류 및 예측 타당성 평가 & 해석 및 예측 14 형성과정
분류 트리 종속변수가 범주형 변수 일 때, 만들어지는 모델(트리) 회귀 트리 종속변수가 연속형 변수 일 때, 만들어지는 모델(트리) Tree를 만드는 기준? 두가지 트리의 만드는 방식은 동일, Split(growing) Rule과 예측하는 방식이 다르다! 15
분류 트리 분리 규칙(Split Rule) 목표 변수가 각 범주에 속하는 빈도에 기초하여 분리가 일어난다. 불순도: 얼마나 다른 범주의 개체들이 포함되어 있는가 - 엔트로피 계수(Entropy index) - 지니 계수(Gini index) - 카이제곱 통계량의 p-value > 불순도가 가장 작은 분할 기준에 따라 Split 16
17 분류 트리 엔트로피 계수 엔트로피 계수가 가장 작은 분할 기준에 따라 자식 마디를 생성 지니 계수 지니 계수를 감소시켜주는 분할 기준에 따라 자식 마디를 생성
18 분류 트리 > Pk: A영역에 속하는 관측치 중 K 집단에 속하는 관측치 비율 G(L) = 1 − 7 8 2 + 1 8 2 = 0.21875 G(R) = 1 − 3 8 2 + 5 8 2 = 0.46875 Gini = 8 16 × 0.21875 + 8 16 × 0.46875 = 0.34375 > Pk: A영역에 속하는 관측치 중 K 집단에 속하는 관측치 비율 Entropy = 8 16 × 0.5436 + 8 16 × 0.9544 = 0.749 E(L) = - 7 8 × log2 7 8 + 1 8 × log2 1 8 = 0.5436 E(R) = - 3 8 × log2 3 8 + 5 8 × log2 5 8 = 0.9544 지니 계수 엔트로피 계수
오분류오차 한쪽 범주에 속한 비율p에 따른 불순도의 변화량을 그래프로 나타낸 것 > 비율이 0.5(두 범주가 각각 반반씩 섞여 있는 경우)일 때 불순도가 최대. 영역 A에 속한 모든 관측치가 동일한 범주에 속할 경우 불확실성 최소 = 순도 최대 엔트로피 = 0 범주가 두가지이고 해당 관측치가 동일하게 반반 섞여 있을 경우 불확실성 최대 = 순도 최소 엔트로피 = 0.5 19
P-value값이 가장 작은 분할 기준에 따라 자식 마디를 생성 > 카이제곱 통계량이 가장 큰 것 (= p-value 값이 가장 작은 것) Good Bad Total Left 32(56) 48(24) 80 Right 178(154) 42(66) 220 Total 210 90 300 각 셀에 대한 ((기대도수 – 실제도수)의 제곱/기대도수)의 합 56−32 2 56 + 24−48 2 24 + 154−178 2 154 + 66−42 2 66 = 46.75 20 카이제곱 통계량 분류 트리
21 분류 트리 Case 1 R1 R2 Case 2 R1 R2 Case 3 R1 R2 A B,C B A,C C A,B Case 별로 지니 계수 혹은 엔트로피 계수를 비교해 가장 작은 값을 갖는 Split rule(case)를 선택한다. 설명 변수: 범주형 (‘A’, ‘B’, ‘C’)일 경우
22 분류 트리 통학시간 >= 60 R1 R2 Yes No 지니계수 혹은 엔트로피 계수를 비교해 가장 작은 값을 갖도록하는 경계값을 찾는다. 설명 변수: 연속형일 경우_ 경계값의 기준을 찾는다. 경계값 후보 Ex1) 1사분위수 / 2사분위수 / 3사분위수 Ex2) seq(from=1사분위수, to=3사분위수, length.out=10) Ex3) seq(from=min(x), to=max(x), length.out=10)
회귀 트리 분리 규칙(Split Rule) 목표 변수의 평균과 표준편차에 기초하여 마디의 분리가 일어난다. 예측값의 종류는 terminal node의 개수와 동일하다. 불순도: 얼마나 다른 범주의 개체들이 포함되어 있는가 - F-통계량의 p-value값 - 분산의 감소량(Variance reduction) > 최소제곱 추정량(SSE)을 줄여 나가는 방식으로 Split 23
최소 제곱 추정량(SSE)을 줄여 나가는 방식으로 split Node1 y11 = 10 y12 = 12 y13 = 13 y14 = 8 y15 = 7 ത 𝑦 = 10 Node2 y21 = 20 y22 = 24 y23 = 26 y24 = 16 y25 = 14 ത 𝑦 = 20 Node1_SSE : 10 − 10 2 + 12 − 10 2 + … + 7 − 10 2 = 26 Node2_SSE : 20 − 20 2 + 24 − 20 2 + … + 14 − 20 2 = 104 SSE의 합: 5 10 × 26 + 5 10 × 104 = 65 SSE를 줄여 나가는 방식으로 split 24 회귀 트리 F-통계량 & 분산의 감소량
25 회귀 트리
26 회귀 트리 X0 X1 X2 X3 Y mse = 각 노드의 MSE값 sample = 부모 노드로부터 내려온 자식 노드의 sample 수 value = 각 노드의 sample들의 y 평균값
정지 규칙 정지규칙(Stop rule) : 분리가 더 이상 일어나지 않도록 하는 기준 1. 더 이상 분리해도 불순도가 줄어들지 않을 경우 2. 자식 마디에 남아 있는 sample 수가 적은 경우 3. 분석자가 미리 정해 놓은 깊이에 도달했을 경우 27
Pruning 적절하지 않은 마디를 제거 > 학습 데이터에 overfitting 문제가 발생할 가능성 존재 > 적당한 크기의 나무 구조를 가지도록 하는 규칙 28
Q. 의사결정 나무의 분류기가 증가하면? A. 새로운 데이터에 대한 오분류율이 감소한다. Q. 계속 분류기를 무한히 증가하면? A. 일정 수준 이상의 분류기를 가질 경우, 오분류율이 오히려 증가한다. 가지치는 시점? >검증 데이터에 대한 오분류율이 증가하는 시점 가지치기는 데이터를 버리는 개념이 아닌 분류기를 합치는 개념으로 이해 29 Pruning
비용복잡도를 최소로 하는 분기를 찾아내도록 학습 CC(T): 의사결정 나무의 비용 복잡도 (= 오류가 적으면서 terminal node수가 적은 단순한 모델일수록 작은 값) Err(T): 검증 데이터에 대한 오분류율(불순도) L(T): 끝마디의 수(구조의 복잡도) a: Err(T)와 L(T)를 결합하는 가중치 (보통 0.01~0.1의 값) 30 비용복잡도(cost-complexity) Pruning
Split할 때 오분류율 + (마디 수 *0.5) 만큼의 오차가 더 있다고 가정 > 과적합을 피하기 위해서 오분류율: 0.45 끝마디 수: 4 Pessimistic error 0.45+4*0.5 = 2.45 오분류율: 0.66 끝마디 수: 3 Pessimistic error 0.66+3*0.5 = 2.16 Tree model을 pruning 했을 때떄 pessimistic error값이 더 낮으므로, pruning 실행 31 Pessimistic pruning Pruning
분류 트리 끝마디의 범주의 voting값으로 예측 회귀 트리 끝마디의 ഥ 𝐲로 예측 Node1 y11 = 10 y12 = 12 y13 = 13 y14 = 8 y15 = 7 ത 𝑦 = 10 Node2 y21 = 20 y22 = 24 y23 = 26 y24 = 16 y25 = 14 ത 𝑦 = 20 Yes: 90 No: 10 Yes: 34 No: 66 yes no 32 해석 및 예측
단점 장점 1. 해석의 용이성 - 나무구조에 의해서 모형이 표현되기 때문에 해석이 쉽다. - 새로운 자료에 모형을 적합 시키기 쉽다. - 어떤 입력변수가 중요한지 파악이 쉽다. 2. 교호작용 효과의 해석 - 두 개 이상의 변수가 결합하여 목표변수에 어떠한 영향을 주는지 알기 쉽다. 3. 비모수적 모형 - 선형성, 정규성, 등분산성의 가정이 필요하지 않다. - 단지 순위만 분석에 영향을 주므로 이상치에 민감하지 않다. 1. 비연속성 - 연속형 변수를 비연속적인 값으로 취급하여 예측오류가 클 가능성이 있다. 2. 선형성 또는 주효과의 결여 - 선형 또는 주효과 모형에서와 같은 결과를 얻을 수 없다. 3. 비안정성 - 분석용 자료에만 의존하므로 새로운 자료의 예측에 불안정하다. 33
정리 Tree는 해석이 용이하고, 의사결정 방법이 인간의 의사결정 방법과 유사하지만, 예측력이 많이 떨어지고, bias-variance 문제가 발생한다. 이를 해결하기 위해! Tree를 여러 개 생성하고 결합하는 Ensemble (bagging, boosting, Random Forest)을 사용하여 Tree의 예측력을 높인다. 34
쉽시다!!!! 35
Ensemble 여러 개의 분류, 회귀 모형을 조합하여 예측의 정확도를 높이는 방법 Bias & variance Trade off를 해결해 error를 낮추는 것이 목적 배깅(Bagging) / 부스팅(Boosting) / 스태킹(Stacking) 36
앙상블을 왜 사용할까? 학습에서의 오류 1. Underfitting(낮은 bias) 2. Overfitting(높은 Variance) 특히 배깅은 각 샘플에서 나타난 결과를 일종의 중간값으로 맞추어 주기 때문에 overfitting을 피할 수 있다. 범주형일 경우, Voting으로 집계 연속형일 경우, Average로 집계 앙상블 기법을 통해 오류를 최소화! 37
앙상블을 왜 사용할까? 38 https://www.youtube.com/watch?v=Un9zObFjBH0
부스팅 Boosting 배깅 Bootstrap AGGregatING (Bagging) 여러 번의 샘플을 뽑아 각 모델을 학습시켜 결과를 집계(Aggregating)하는 방법 Random Forest 약한 학습 결과를 합쳐 강한 학습 결과를 만드는 방법 AdaBoost / XGBoost GBM / Light GBM 39
40
Bagging Bagging: Bootstrap aggregating의 준말. (Bootstrap: 데이터에서 일부를 샘플링하는 것) - 원 데이터 집합으로부터 크기가 같은 표본을 여러 번 단순 임의 복원 추출하여 각 표본에 대해 분류기를 생성한 후 그 결과를 앙상블 하는 방법 - 반복 추출 방법을 사용하기 때문에 같은 데이터가 한 표본에 여러 번 추출 될 수도, 어떤 데이터는 추출되지 않을 수도 있다. - 하나의 학습 데이터에 overfitting 되어 테스트 데이터에서 성능이 낮을 경우 즉, high variance일 경우를 여러 개의 학습 데이터를 만들어 결합함으로써 low variance로 변화시켜 예측 성능을 향상시킨다. 41
1. n번 단순 임의 복원 추출 Bagging 42 A B C D Train data A A A B B D D D C C C C . . . Bootstrap sample1 Bootstrap sample2 Bootstrap sample3
2. 여러 개의 단일 모델 생성 Bagging 43 A A A B B D D D C C C C . . . training training training model1 model2 model3 . . . 범주형: voting 연속형: averaging
Bagging 44
Bagging 45 https://www.youtube.com/watch?time_continue=1&v=2Mg8QD0F1dQ
Bagging > Variance를 낮추기 좋다. 서로 다른 여러 개의 모델들의 결과들을 모두 고려하여 최종 결과를 내기 때문에 하나의 trainset에 너무 치중된 상태에서 train이 되는 경우(overfitting)를 피할 수 있다. 동시에 모델의 높은 정확도도 유지할 수 있다. >> 과적합 우려가 큰 (=variance가 큰) 머신러닝 기법들에 적용하기 좋은 앙상블 방법이다. 46
Bagging 랜덤 포레스트(Random Forest) > 의사결정나무에 배깅을 적용한 모형 = Data Bagging + Feature Bagging + Decision Tree Data Bagging > 데이터를 임의 단순 복원 추출 시행(일반적인 배깅) Feature Bagging(특성 배깅) > 변수를 임의 단순 복원 추출 (무작위로 선택된 특성을 이용=임의 노드 최적화) Decision Tree > 의사결정 나무(CART) 47 Random Forest
Bagging 48 Random Forest = Data Bagging + Feature Bagging + Decision Tree 온도 습도 풍속 비 여부 A 15 60 15 1 B 21 10 1 1 C 3 70 5 0 D 7 2 30 0 온도 습도 비 여부 A 15 60 1 A 15 60 1 C 3 70 0 A 15 60 1 습도 풍속 비 여부 D 2 30 0 B 10 1 1 C 70 5 0 C 70 5 0 Tree1 Tree2 Tree correlation(모두 동일한 변수를 가져왔을 때 생기는 문제)이 높아지는 것을 방지하기 위해 feature bagging 실행
Bagging Random Forest 성능평가 OOB(Out-Of-Bag) error > 부트스트랩 샘플링 과정에서 추출되지 않은 데이터들을 따로 랜덤포레스트로 학습시켜 나온 결과 > OOB 샘플들은 주로 평가용 데이터에서의 오분류율을 예측하는 용도 및 변수 중요도를 추정하는 용도로 많이 이용된다. 49
Bagging Random Forest Random Forest 중요 특징: 변수 중요도 - 데이터 분석 시 가장 중요한 issue 중 하나는 변수 선택! - Feature bagging을 적용하는 Random Forest는 각 변수들의 중요성에 순위를 매길 수 있다. - Random Forest 구성 과정에서 각 feature에 대한 OOB-오차(Out-Of-Bag error)가 구해진다. (OOB: Bootstrap을 통한 임의 중복 추출 시 각 feature에 대한 test data) - 분류의 경우, 해당 변수로 부터 분할이 일어날 때 불순도의 감소가 얼마나 일어나는지에 따라 변수 중요도 결정 - 회귀의 경우, 잔차제곱합을 통해 변수 중요도 측정 50
Bagging Random Forest 51
Boosting Boosting Bootstrap 샘플링 이후, 분류 결과를 이용하여 분류가 잘못된 데이터에 더 큰 가중치를 부여하여 표본을 추출하는 방법 > Bagging은 병렬로 학습하는 반면, Boosting은 순차적으로 학습 > 학습이 끝나면 나온 결과에 따라 가중치 재분배 > 오답에 대해 높은 가중치를 부여하고 정답에 대해 낮은 가중치를 부여하여 오답에 더욱 집중할 수 있도록 한다. 52
Boosting 53
Boosting 54 알고리즘 특징 비고 AdaBoost - 오분류에 대해 가중치 부여 2003 GBM - Loss Function의 gradient를 통해 오답에 가중치 부여 2007 XGBoost - GBM 대비 성능 향상 - 시스템 자원 효율적 활용(CPU, Mem) - Kaggle을 통한 성능 검증 2014 Light GBM - XGBoost 대비 성능 향상 및 자원소모 최소화 - XGBoost가 처리하지 못하는 대용량 데이터 학습 가능 - Approximates the split(근사치의 분할)을 통한 성능 향상 2016
Boosting AdaBoost 0. 배깅과 동일하게 샘플 데이터 추출 1. 하나의 모형 학습(Box1) 2. 학습 결과로 예측하여 틀린 사례에 큰 가중치 부여하고 다시 학습(Box2) 3. 이 과정을 반복(Box3)하여 학습 결과를 합친다.(Box4) > 잡음이 많은 데이터와 이상점에 취약하다. AdaBoost 55
1. 1회 복원추출 후 트리 모델 생성 AdaBoost 56 A B C D Train data A C D Tree 1 Bagging과 동일 A
2. 가중치 업데이트 AdaBoost 57 B C D A B C D Train data Train_Data로 test를 한 후, 오분류된 데이터들이 추출될 확률을 높인 후 1번 과정을 다시 시행 가중치 A 1 4 B 1 4 C 1 4 D 1 4 업데이트된 가중치 A 1 4 ∗ exp(−𝑎)/(𝐴 + 𝐵 + 𝐶 + 𝐷) B 1 4 ∗ exp(𝑎)/(𝐴 + 𝐵 + 𝐶 + 𝐷) C 1 4 ∗ exp(−𝑎)/(𝐴 + 𝐵 + 𝐶 + 𝐷) D 1 4 ∗ exp(−𝑎)/(𝐴 + 𝐵 + 𝐶 + 𝐷) B Tree 2 #. e(에러율): 오류데이터 가중치 합 / 전체 데이터 가중치 합 #. a(신뢰도): 1 2 ∗ ln( 1−𝑒 𝑒 ) B만 오분류된 상태
3. 위 과정 반복 AdaBoost 58 에러율이 0이 될 때까지 혹은 트리 모델 수가 일정한 수에 도달할 때까지 위 과정들을 계속 반복 . . . A B C D Train data D C D B B C D B C Tree 1 Tree 2 Tree 3 A A A
4. 신뢰도(a)를 곱하여 voting AdaBoost 59 Tree 1 Predict*a Tree 2 Predict*a Tree 3 Predict*a . . . . . . + + =
Boosting AdaBoost 60 https://www.youtube.com/watch?v=GM3CDQfQ4sw
Boosting GBM GBM(Gradient Boosting) = 경사 부스팅 > 이전의 학습 결과와 실제의 차이를 학습하는 방식 > 가중치 계산 방식에서 Gradient Descent를 적용 두번째 학습 결과 f2가 첫번째 예측 오차를 학습 첫번째 학습 결과 f1 학습이 잘 되었다면, 첫번째 학습 오차분산 Var(e1)보다 두번째 학습의 오차분산 Var(e2)가 더 줄어들게 된다. 61
Boosting GBM 학습기 M에 대해서 Y를 예측할 확률 > Y = M(x) + error > error = G(x) + error2 (error > error2) > error2 = H(x) + error3 (error2 > error3) > Y = M(x) + G(x) + H(x) + error3 학습기 M을 단독으로 사용했을 때보다 정확도가 높을 것이다. (error > error3) Error를 세분화 62
Boosting GBM 학습기 M을 단독으로 사용했을 때보다 정확도가 높을 것이다. (error > error3) Error를 세분화 63 M, G, H 각각 분류기의 성능이 다른데, 모두 같은 비중을 두고 있기 때문에 임의의 x에 대해 서로 간섭하여 오류를 높이는 결과를 가져올 수 있다. 학습기 M에 대해서 Y를 예측할 확률 > Y = M(x) + error > error = G(x) + error2 (error > error2) > error2 = H(x) + error3 (error2 > error3) > Y = M(x) + G(x) + H(x) + error3
Boosting GBM 각 함수별 최적의 가중치를 찾으면, 예측 정확도 향상 (Gradient Descent 알고리즘으로 최적 weight값 계산) Y = alpha * M(x) + beta * G(x) + gamma * H(x) + error3 64
Boosting GBM 가중치 부여 방식? > 초기 데이터 가중치(D) = 1/n (n: 전체 학습 데이터 개수) > 오류(e): 오류데이터 / 전체 학습 데이터 > Weak model의 함수: h(t) (=모델의 예측값) > 가중치 업데이트(D) > 모델의 가중치(a) (=learning rate역할) 65
Boosting XGBoost - GBM + 분산/병렬 처리 - Split 지점을 고려할 때 일부를 보고 결정 - Sparsity Awareness가 가능 - Binary classification / Multiclass classification / Regression / Learning to Rank XGBoost (eXtreme Gradient Boosting) > 목적함수를 정의하고 이를 최소화 하는 값을 찾아 가중치를 업그레이드 > 지도학습으로 변수(x)를 학습하여 정답(y)을 예측 66
Boosting XGBoost > CPU 병렬처리, 코어들이 각자 할당 받은 변수들로 제각기 가지를 쳐 나간다. > 연산시간 단축 67
Boosting XGBoost > 연속형 변수에서 split 지점을 고려할 때 모든 값들을 살펴보고 결정하기 보단 일부분만을 보고 결정을 한다. ID 국어 수학 1 100 90 2 95 80 3 75 90 4 20 55 일부 후보군만 보고 split 지점 결정 68
Boosting XGBoost > Sparsity Awareness가 가능 > Zero 데이터를 건너뛰면서 학습이 가능하다. > Input을 dummy화 하면 속도가 상승! ID 과목 1 국어 2 수학 3 영어 4 과학 ID 국어 수학 영어 과학 1 1 0 0 0 2 0 1 0 0 3 0 0 1 0 4 0 0 0 1 69
Boosting Light GBM 70 Light GBM > Decision Tree 알고리즘 기반의 GBM 프레임워크 (속도, 성능 향상) > Ranking, Classification등의 문제에 활용 다른 tree 알고리즘과의 차이점? - Leaf-wise로 tree를 성장(수직 방향) - 최대 delta loss의 leaf를 성장 즉, 동일한 leaf를 성장시킬 때, leaf-wise가 loss를 더 줄일 수 있다. https://www.slideshare.net/freepsw/boosting-bagging-vs-boosting
Boosting Light GBM 71 Leaf-wise(Light GBM) > 가장 loss변화가 큰 노드에서 데이터를 분할 > 학습 데이터가 많은 경우 뛰어난 성능 > 수직 성장 Level-wise(XGBoost, Random Forest) > 각 노드는 root 노드와 가까운 노드를 우선 순회 > 수평 성장
Boosting Light GBM 72 왜 Light GBM이 인기가 있을까? > 대량의 데이터를 병렬로 빠르게 학습이 가능하다.(Low memory, GPU 활용가능) > 예측 정확도가 더 높다. (Leaf-wise tree의 장점: 과적합에 민감) 특징 > XGBoost의 2~10배 (동일한 파라미터로 설정)빠르다. > Leaf-wise tree는 overfitting에 민감하여, 대량의 데이터 학습에 적합하다. (적어도 10,000개 이상의 행이 있는 데이터에 적합하다.)
Stacking “Two heads are better than one” = Meta modeling 여러 모델들의 결과값을 averaging, voting하여 새로운 결과값 생성 여러 모델들의 결과값을 새로운 변수로 데이터셋 생성 (이후 다시 모델 학습) 73
Stacking > 여러 모델들의 결과값을 averaging, voting하여 새로운 결과값 생성 종속변수: 범주형 - Predict 값 중 확률 값들을 평균내 최종 예측 값으로 사용 - 예측 값 자체를 voting하여 최종 예측 값으로 사용 종속변수: 연속형 - 예측 값 자체를 averaging하여 최종 예측 값으로 사용 74
Stacking > 여러 모델들의 결과값을 새로운 변수로 데이터셋 생성 (이후 다시 모델 학습) 종속변수: 범주형 - Predict 값 중 확률 값들을 새로운 변수로 사용 - 예측 값 자체를 새로운 변수로 사용 종속변수: 연속형 - 예측 값 자체를 새로운 변수로 사용 75
Train Test predict Model 1 Train Test Model 3 Voting or Averaging 76 Stacking Train Test Model 2 predict predict predict
Stacking Train Test predict Model 1 Train Test feature1 새로운 변수로 데이터셋 생성 77 Train Test predict Model 2 feature2
Q & A
Decision tree and ensemble

More Related Content

PDF
Understanding random forests
byMarc Garcia
 
PDF
Tree models with Scikit-Learn: Great models with little assumptions
byGilles Louppe
 
PPT
Unit 3classification
byKalpna Saharan
 
PPTX
Decision Trees for Classification: A Machine Learning Algorithm
byPalin analytics
 
PDF
Random forest sgv_ai_talk_oct_2_2018
bydigitalzombie
 
PPTX
Random Forest Classifier in Machine Learning | Palin Analytics
byPalin analytics
 
PPTX
Random forest r_packages_slides_02-02-2018_eng
byShuma Ishigami
 
PPTX
Random Forest and KNN is fun
byZhen Li
 
Understanding random forests
byMarc Garcia
 
Tree models with Scikit-Learn: Great models with little assumptions
byGilles Louppe
 
Unit 3classification
byKalpna Saharan
 
Decision Trees for Classification: A Machine Learning Algorithm
byPalin analytics
 
Random forest sgv_ai_talk_oct_2_2018
bydigitalzombie
 
Random Forest Classifier in Machine Learning | Palin Analytics
byPalin analytics
 
Random forest r_packages_slides_02-02-2018_eng
byShuma Ishigami
 
Random Forest and KNN is fun
byZhen Li
 

What's hot

PDF
Lec 8 03_sept [compatibility mode]
byPalak Sanghani
 
PPTX
Classification decision tree
byyazad dumasia
 
PDF
ID3 Algorithm & ROC Analysis
byTalha Kabakus
 
PPT
Cs221 lecture5-fall11
bydarwinrlo
 
PPTX
Decision tree
byTilani Gunawardena PhD(UNIBAS), BSc(Pera), FHEA(UK), CEng, MIESL
 
PPTX
Ensemble methods in machine learning
bySANTHOSH RAJA M G
 
PPTX
Comparison Study of Decision Tree Ensembles for Regression
bySeonho Park
 
PPTX
Decision Tree and Bayesian Classification
byKomal Kotak
 
PPT
Cs583 association-rules
byGautam Thakur
 
PDF
Ultra Violet-Visable Spectroscopy Analysis of Spin Coated Substrates
byNicholas Lauer
 
PPT
Association rule mining
byAcad
 
Lec 8 03_sept [compatibility mode]
byPalak Sanghani
 
Classification decision tree
byyazad dumasia
 
ID3 Algorithm & ROC Analysis
byTalha Kabakus
 
Cs221 lecture5-fall11
bydarwinrlo
 
Decision tree
byTilani Gunawardena PhD(UNIBAS), BSc(Pera), FHEA(UK), CEng, MIESL
 
Ensemble methods in machine learning
bySANTHOSH RAJA M G
 
Comparison Study of Decision Tree Ensembles for Regression
bySeonho Park
 
Decision Tree and Bayesian Classification
byKomal Kotak
 
Cs583 association-rules
byGautam Thakur
 
Ultra Violet-Visable Spectroscopy Analysis of Spin Coated Substrates
byNicholas Lauer
 
Association rule mining
byAcad
 

Similar to Decision tree and ensemble

PDF
Decision Tree Intro [의사결정나무]
byHyunwoo Kim
 
PDF
Decision tree
bySEMINARGROOT
 
PDF
Outlier Analysis.pdf
byH K Yoon
 
PPT
Machine learning........................
byssuserc13e6a
 
PDF
AI 바이오 (2_3일차).pdf
byH K Yoon
 
PDF
Incheon National University - EATED SRA
byssuser58d6dc2
 
PDF
Support vector machines
byJinho Lee
 
PDF
제 14회 보아즈(BOAZ) 빅데이터 컨퍼런스 - [BICS팀] : Boaz Industry Classification Standard
byBOAZ Bigdata
 
PPTX
Machine learning
bysujinkim136
 
PPTX
Deep Learning for AI (2)
byDongheon Lee
 
PDF
1시간만에 머신러닝 개념 따라 잡기
bySungmin Kim
 
PDF
집단지성 프로그래밍 08-가격모델링
byKwang Woo NAM
 
PPTX
Detailed Description on Cross Entropy Loss Function
by범준 김
 
PDF
Introduction to e tapr for hai con -kor
byDACON AI 데이콘
 
PDF
SRA final project
byssuser542c21
 
PPTX
Murpy's Machine Learning:14. Kernel
byJungkyu Lee
 
PDF
Regularizing Class-wise Predictions via Self-knowledge Distillation
bySungchul Kim
 
PPTX
Seminar9
bykim taegong
 
PPTX
Elementary statistical inference1
bySEMINARGROOT
 
PPTX
R v01 rprogamming_basic01 (R 프로그래밍 기본)
byBuskersBu
 
Decision Tree Intro [의사결정나무]
byHyunwoo Kim
 
Decision tree
bySEMINARGROOT
 
Outlier Analysis.pdf
byH K Yoon
 
Machine learning........................
byssuserc13e6a
 
AI 바이오 (2_3일차).pdf
byH K Yoon
 
Incheon National University - EATED SRA
byssuser58d6dc2
 
Support vector machines
byJinho Lee
 
제 14회 보아즈(BOAZ) 빅데이터 컨퍼런스 - [BICS팀] : Boaz Industry Classification Standard
byBOAZ Bigdata
 
Machine learning
bysujinkim136
 
Deep Learning for AI (2)
byDongheon Lee
 
1시간만에 머신러닝 개념 따라 잡기
bySungmin Kim
 
집단지성 프로그래밍 08-가격모델링
byKwang Woo NAM
 
Detailed Description on Cross Entropy Loss Function
by범준 김
 
Introduction to e tapr for hai con -kor
byDACON AI 데이콘
 
SRA final project
byssuser542c21
 
Murpy's Machine Learning:14. Kernel
byJungkyu Lee
 
Regularizing Class-wise Predictions via Self-knowledge Distillation
bySungchul Kim
 
Seminar9
bykim taegong
 
Elementary statistical inference1
bySEMINARGROOT
 
R v01 rprogamming_basic01 (R 프로그래밍 기본)
byBuskersBu
 

More from Danbi Cho

PDF
Crf based named entity recognition using a korean lexical semantic network
byDanbi Cho
 
PDF
Gpt models
byDanbi Cho
 
PDF
Attention boosted deep networks for video classification
byDanbi Cho
 
PDF
A survey on deep learning based approaches for action and gesture recognition...
byDanbi Cho
 
PDF
ELECTRA_Pretraining Text Encoders as Discriminators rather than Generators
byDanbi Cho
 
PDF
A survey on automatic detection of hate speech in text
byDanbi Cho
 
PDF
Zero wall detecting zero-day web attacks through encoder-decoder recurrent ne...
byDanbi Cho
 
PDF
Can recurrent neural networks warp time
byDanbi Cho
 
PDF
Man is to computer programmer as woman is to homemaker debiasing word embeddings
byDanbi Cho
 
PDF
Situation recognition visual semantic role labeling for image understanding
byDanbi Cho
 
PDF
Mitigating unwanted biases with adversarial learning
byDanbi Cho
 
Crf based named entity recognition using a korean lexical semantic network
byDanbi Cho
 
Gpt models
byDanbi Cho
 
Attention boosted deep networks for video classification
byDanbi Cho
 
A survey on deep learning based approaches for action and gesture recognition...
byDanbi Cho
 
ELECTRA_Pretraining Text Encoders as Discriminators rather than Generators
byDanbi Cho
 
A survey on automatic detection of hate speech in text
byDanbi Cho
 
Zero wall detecting zero-day web attacks through encoder-decoder recurrent ne...
byDanbi Cho
 
Can recurrent neural networks warp time
byDanbi Cho
 
Man is to computer programmer as woman is to homemaker debiasing word embeddings
byDanbi Cho
 
Situation recognition visual semantic role labeling for image understanding
byDanbi Cho
 
Mitigating unwanted biases with adversarial learning
byDanbi Cho
 

Recently uploaded

PDF
Malware_Detection_A_Framework_for_Reverse_Engineered_Android_Applications_Thr...
byKiritiyadavGoskula
 
PDF
What-Every-Tech-Leader-Needs-to-Know-About-AI-in-2025.pdf
byrishabhxbohra
 
PDF
Projectlify: Everything You Need to Get Things Done
byRafal Ksiazek
 
PDF
contusion pulmonar y antibiotico en el atls
byMARIAPETRONILAMONTAO
 
PDF
IoT/OT Security: Penetration Testing for an Expanding Attack Surface.pdf
byCybernetic Global Intelligence
 
PDF
Introduction to Microsoft 365 Security and Compliance.pdf
byjohnsonsouza5
 
PDF
Postmates Clone App Delivery Service Business Solution.pdf
byV3CUBE TECHNOLABS
 
PDF
Edge AI vs Cloud AI: Why Frontend Developers Must Master On-Device Machine Le...
byWorkfall hire developers
 
PDF
A Complete Guide to Progressive Web App and Their Development
byMaxtra Technologies
 
PPTX
wAIred_RabobankWRProducts__22012026.pptx
bySimonedeGijt
 
PPTX
apidays Australia 2025 | Advanced GraphQL Security with AI Driven Threat Dete...
byapidays
 
PDF
apidays Australia 2025 | Designing with workflows: Using Arazzo and OpenAPI f...
byapidays
 
PDF
09920-2 JE40CP MB 48.4GY02.021 Schematic Acer Aspire 4741.pdf
bydakjuel1
 
PDF
apidays Australia 2025 | APIs in Government: A blueprint to automating Busine...
byapidays
 
PDF
Salesforce Careers in 2026_ Trends, Certifications, and Must-Have Skills
byDele Amefo
 
PDF
Gojek Clone Business Strategy: From Launch to Scale
byV3CUBE TECHNOLABS
 
PPTX
Anomalies in Relational Database Management systems.pptx
byamutham12
 
PPTX
apidays Australia 2025 | Hey man, which one will deploy much faster, API or kid?
byapidays
 
Malware_Detection_A_Framework_for_Reverse_Engineered_Android_Applications_Thr...
byKiritiyadavGoskula
 
What-Every-Tech-Leader-Needs-to-Know-About-AI-in-2025.pdf
byrishabhxbohra
 
Projectlify: Everything You Need to Get Things Done
byRafal Ksiazek
 
contusion pulmonar y antibiotico en el atls
byMARIAPETRONILAMONTAO
 
IoT/OT Security: Penetration Testing for an Expanding Attack Surface.pdf
byCybernetic Global Intelligence
 
Introduction to Microsoft 365 Security and Compliance.pdf
byjohnsonsouza5
 
Postmates Clone App Delivery Service Business Solution.pdf
byV3CUBE TECHNOLABS
 
Edge AI vs Cloud AI: Why Frontend Developers Must Master On-Device Machine Le...
byWorkfall hire developers
 
A Complete Guide to Progressive Web App and Their Development
byMaxtra Technologies
 
wAIred_RabobankWRProducts__22012026.pptx
bySimonedeGijt
 
apidays Australia 2025 | Advanced GraphQL Security with AI Driven Threat Dete...
byapidays
 
apidays Australia 2025 | Designing with workflows: Using Arazzo and OpenAPI f...
byapidays
 
09920-2 JE40CP MB 48.4GY02.021 Schematic Acer Aspire 4741.pdf
bydakjuel1
 
apidays Australia 2025 | APIs in Government: A blueprint to automating Busine...
byapidays
 
Salesforce Careers in 2026_ Trends, Certifications, and Must-Have Skills
byDele Amefo
 
Gojek Clone Business Strategy: From Launch to Scale
byV3CUBE TECHNOLABS
 
Anomalies in Relational Database Management systems.pptx
byamutham12
 
apidays Australia 2025 | Hey man, which one will deploy much faster, API or kid?
byapidays
 

Decision tree and ensemble

  • 1.
  • 2.
    01 02 03 배깅부스팅 스태킹 01 02 03 모델 형성과정 정리
  • 3.
    Decision Tree 분류 /예측을 하는 지도학습 방법론 의사결정 규칙(Decision Rule)에 따라서 Tree를 생성한 후에 분류 / 예측하는 방법론 3
  • 4.
    목적 1). 세분화(Segmentation) 데이터를 비슷한특성을 갖는 몇 개의 그룹으로 분할, 그룹별 특성을 발견하는 경우 또는 각 데이터가 어떤 집단에 속하는지를 파악하고자 하는 경우 Ex) 시장 세분화, 고객 세분화 2). 분류(Classification) 관측개체를 여러 예측변수들에 근거해 목표변수의 범주를 몇 개의 등급으로 분류하고자 하는 경우 Ex) 고객을 신용도에 따라 우량/불량으로 분류 3). 예측(Prediction) 자료에서 규칙을 찾아내고 이를 이용해 미래의 사건을 예측하고자 하는 경우 Ex) 고객속성에 따라 대출한도액을 예측 4). 차원축소 및 변수선택(Data reduction and variable screening) 매우 많은 수의 예측변수 중에서 목표변수에 큰 영향을 미치는 변수들을 골라내고자 하는 경우 5). 교호작용효과의 파악(Interaction effect identification) 여러 개의 예측변수들을 결합해 목표변수에 작용하는 규칙(교호작용효과)을 파악하고자 하는 경우 6). 범주의 병합 또는 연속형 변수의 이산화(Binning) 범주형 목표변수의 범주를 소수의 몇 개로 병합하거나 연속형 목표변수를 몇 개의 등급으로 이산화 하고자 하는 경우 4
  • 5.
    부모마디(parent node) > 자식마디의상위마디 자식마디(child node) > 하나의 마디로부터 분리되어 나간 마디 깊이(depth) > 가지를 이루고 있는 마디의 개수 가지(branch) > 하나의 마디로부터 끝마디까지 연결된 마디들 부모마디 자식마디 깊이:3 5
  • 6.
    뿌리마디 중간마디 끝마디 뿌리마디(root node) > 나무구조가시작되는 마디 > 시작되는 마디로 전체 자료가 포함 중간마디(internal node) > 중간에 있는 끝마디가 아닌 마디 > 부모마디와 자식마디가 모두 있는 마디 끝마디(terminal node, leaf) > 각 나무줄기의 끝에 위치하는 마디 > 자식마디가 없는 마디 6
  • 7.
    이름 통학시간(분) 양치질마스크 감기 이예찬 40 X O No 김영도 35 O O No 박정현 110 O X Yes 김태희 85 O O No 홍지민 100 X O Yes 종속변수 Ex) 감기 유무를 맞추자! 7
  • 8.
    8 Train_data 이름 통학시간(분) 양치질마스크 감기 이예찬 40 X O No 김영도 35 O O No 박정현 110 O X Yes 김태희 85 O O No 홍지민 100 X O Yes 통학시간 >= 60 양치질 여부 감기: No 감기: Yes 마스크 여부 No Yes No Yes 감기: Yes 감기: No No Yes
  • 9.
    Train_data를 완벽 분류! 정확도=1 성능좋은 Tree 9 Train_data 이예찬 김영도 홍지민 박정현 김태희 이름 통학시간(분) 양치질 마스크 감기 이예찬 40 X O No 김영도 35 O O No 박정현 110 O X Yes 김태희 85 O O No 홍지민 100 X O Yes 통학시간 >= 60 양치질 여부 감기: No 감기: Yes 마스크 여부 No Yes No Yes 감기: Yes 감기: No No Yes
  • 10.
    10 Train_data 이예찬 김영도 홍지민 박정현 김태희 조단비 50O X No Test_data 이름 통학시간(분) 양치질 마스크 감기 이예찬 40 X O No 김영도 35 O O No 박정현 110 O X Yes 김태희 85 O O No 홍지민 100 X O Yes 통학시간 >= 60 양치질 여부 감기: No 감기: Yes 마스크 여부 No Yes No Yes 감기: Yes 감기: No No Yes 조단비?? -> 오분류
  • 11.
    11 Train_data 이예찬 김영도 홍지민 조단비 50 OX No Test_data 이름 통학시간(분) 양치질 마스크 감기 이예찬 40 X O No 김영도 35 O O No 박정현 110 O X Yes 김태희 85 O O No 홍지민 100 X O Yes 통학시간 >= 60 양치질 여부 감기: No 감기: Yes 감기: No No Yes No Yes 김태희 조단비 질문 1개를 덜 했더라면? Train_data를 완벽하게 분류하진 못하지만 Test_data를 맞출 수 있다. “어떤 기준으로 질문을 해야할까?” “어떤 기준으로 질문을 잘라야 할까?”
  • 12.
    분석의 목적과 자료구조에따라서 적절한 분할기준과 정지규칙을 지정하고 예측값을 할당하여 의사결정 나무를 얻는다. 의사결정나무의 형성 “뿌리마디의 질문이 왜 남자인가” > 분할기준 “끝마디의 위치가 왜 다른가＂ > 정지규칙 “최종 분류(예측)시 어떤 값을 할당하는가“ > 예측값 할당 12 형성과정
  • 13.
    Split Rule(Growing Rule):Tree의 분리 규칙/ 성장 규칙 - 부모 마디로부터 자식 마디를 생성하는 기준 - 순수도: 목표변수의 특정 범주에 개체들이 포함되어 있는 정도 - 목표 변수 구별 정도를 순수도 or 불순도에 의해서 측정 - 순수도가 증가할수록 분할기준에 따라 자식마디 형성 Stop Rule: 정지 규칙 - 분리가 더 이상 일어나지 않도록 하는 기준 Pruning: 가지치기 - Tree가 지나치게 많은 마디를 가지고 있을 경우, overfitting의 문제 발생 - 부적절한 마디를 잘라내 모형을 단순화 13 의사결정나무의 형성 형성과정
  • 14.
    타당성 평가 이익도표(Gain chart)나위험도표(Risk chart) 또는 Cross validation을 이용해서 tree 평가 해석 및 예측 생성한 Tree에 새로운 데이터 대입 후, 분류 및 예측 타당성 평가 & 해석 및 예측 14 형성과정
  • 15.
    분류 트리 종속변수가 범주형변수 일 때, 만들어지는 모델(트리) 회귀 트리 종속변수가 연속형 변수 일 때, 만들어지는 모델(트리) Tree를 만드는 기준? 두가지 트리의 만드는 방식은 동일, Split(growing) Rule과 예측하는 방식이 다르다! 15
  • 16.
    분류 트리 분리 규칙(SplitRule) 목표 변수가 각 범주에 속하는 빈도에 기초하여 분리가 일어난다. 불순도: 얼마나 다른 범주의 개체들이 포함되어 있는가 - 엔트로피 계수(Entropy index) - 지니 계수(Gini index) - 카이제곱 통계량의 p-value > 불순도가 가장 작은 분할 기준에 따라 Split 16
  • 17.
    17 분류 트리 엔트로피 계수 엔트로피계수가 가장 작은 분할 기준에 따라 자식 마디를 생성 지니 계수 지니 계수를 감소시켜주는 분할 기준에 따라 자식 마디를 생성
  • 18.
    18 분류 트리 > Pk:A영역에 속하는 관측치 중 K 집단에 속하는 관측치 비율 G(L) = 1 − 7 8 2 + 1 8 2 = 0.21875 G(R) = 1 − 3 8 2 + 5 8 2 = 0.46875 Gini = 8 16 × 0.21875 + 8 16 × 0.46875 = 0.34375 > Pk: A영역에 속하는 관측치 중 K 집단에 속하는 관측치 비율 Entropy = 8 16 × 0.5436 + 8 16 × 0.9544 = 0.749 E(L) = - 7 8 × log2 7 8 + 1 8 × log2 1 8 = 0.5436 E(R) = - 3 8 × log2 3 8 + 5 8 × log2 5 8 = 0.9544 지니 계수 엔트로피 계수
  • 19.
    오분류오차 한쪽 범주에 속한비율p에 따른 불순도의 변화량을 그래프로 나타낸 것 > 비율이 0.5(두 범주가 각각 반반씩 섞여 있는 경우)일 때 불순도가 최대. 영역 A에 속한 모든 관측치가 동일한 범주에 속할 경우 불확실성 최소 = 순도 최대 엔트로피 = 0 범주가 두가지이고 해당 관측치가 동일하게 반반 섞여 있을 경우 불확실성 최대 = 순도 최소 엔트로피 = 0.5 19
  • 20.
    P-value값이 가장 작은분할 기준에 따라 자식 마디를 생성 > 카이제곱 통계량이 가장 큰 것 (= p-value 값이 가장 작은 것) Good Bad Total Left 32(56) 48(24) 80 Right 178(154) 42(66) 220 Total 210 90 300 각 셀에 대한 ((기대도수 – 실제도수)의 제곱/기대도수)의 합 56−32 2 56 + 24−48 2 24 + 154−178 2 154 + 66−42 2 66 = 46.75 20 카이제곱 통계량 분류 트리
  • 21.
    21 분류 트리 Case 1 R1R2 Case 2 R1 R2 Case 3 R1 R2 A B,C B A,C C A,B Case 별로 지니 계수 혹은 엔트로피 계수를 비교해 가장 작은 값을 갖는 Split rule(case)를 선택한다. 설명 변수: 범주형 (‘A’, ‘B’, ‘C’)일 경우
  • 22.
    22 분류 트리 통학시간 >=60 R1 R2 Yes No 지니계수 혹은 엔트로피 계수를 비교해 가장 작은 값을 갖도록하는 경계값을 찾는다. 설명 변수: 연속형일 경우_ 경계값의 기준을 찾는다. 경계값 후보 Ex1) 1사분위수 / 2사분위수 / 3사분위수 Ex2) seq(from=1사분위수, to=3사분위수, length.out=10) Ex3) seq(from=min(x), to=max(x), length.out=10)
  • 23.
    회귀 트리 분리 규칙(SplitRule) 목표 변수의 평균과 표준편차에 기초하여 마디의 분리가 일어난다. 예측값의 종류는 terminal node의 개수와 동일하다. 불순도: 얼마나 다른 범주의 개체들이 포함되어 있는가 - F-통계량의 p-value값 - 분산의 감소량(Variance reduction) > 최소제곱 추정량(SSE)을 줄여 나가는 방식으로 Split 23
  • 24.
    최소 제곱 추정량(SSE)을줄여 나가는 방식으로 split Node1 y11 = 10 y12 = 12 y13 = 13 y14 = 8 y15 = 7 ത 𝑦 = 10 Node2 y21 = 20 y22 = 24 y23 = 26 y24 = 16 y25 = 14 ത 𝑦 = 20 Node1_SSE : 10 − 10 2 + 12 − 10 2 + … + 7 − 10 2 = 26 Node2_SSE : 20 − 20 2 + 24 − 20 2 + … + 14 − 20 2 = 104 SSE의 합: 5 10 × 26 + 5 10 × 104 = 65 SSE를 줄여 나가는 방식으로 split 24 회귀 트리 F-통계량 & 분산의 감소량
  • 25.
  • 26.
    26 회귀 트리 X0 X1X2 X3 Y mse = 각 노드의 MSE값 sample = 부모 노드로부터 내려온 자식 노드의 sample 수 value = 각 노드의 sample들의 y 평균값
  • 27.
    정지 규칙 정지규칙(Stop rule) :분리가 더 이상 일어나지 않도록 하는 기준 1. 더 이상 분리해도 불순도가 줄어들지 않을 경우 2. 자식 마디에 남아 있는 sample 수가 적은 경우 3. 분석자가 미리 정해 놓은 깊이에 도달했을 경우 27
  • 28.
    Pruning 적절하지 않은 마디를제거 > 학습 데이터에 overfitting 문제가 발생할 가능성 존재 > 적당한 크기의 나무 구조를 가지도록 하는 규칙 28
  • 29.
    Q. 의사결정 나무의 분류기가증가하면? A. 새로운 데이터에 대한 오분류율이 감소한다. Q. 계속 분류기를 무한히 증가하면? A. 일정 수준 이상의 분류기를 가질 경우, 오분류율이 오히려 증가한다. 가지치는 시점? >검증 데이터에 대한 오분류율이 증가하는 시점 가지치기는 데이터를 버리는 개념이 아닌 분류기를 합치는 개념으로 이해 29 Pruning
  • 30.
    비용복잡도를 최소로 하는분기를 찾아내도록 학습 CC(T): 의사결정 나무의 비용 복잡도 (= 오류가 적으면서 terminal node수가 적은 단순한 모델일수록 작은 값) Err(T): 검증 데이터에 대한 오분류율(불순도) L(T): 끝마디의 수(구조의 복잡도) a: Err(T)와 L(T)를 결합하는 가중치 (보통 0.01~0.1의 값) 30 비용복잡도(cost-complexity) Pruning
  • 31.
    Split할 때 오분류율+ (마디 수 *0.5) 만큼의 오차가 더 있다고 가정 > 과적합을 피하기 위해서 오분류율: 0.45 끝마디 수: 4 Pessimistic error 0.45+4*0.5 = 2.45 오분류율: 0.66 끝마디 수: 3 Pessimistic error 0.66+3*0.5 = 2.16 Tree model을 pruning 했을 때떄 pessimistic error값이 더 낮으므로, pruning 실행 31 Pessimistic pruning Pruning
  • 32.
    분류 트리 끝마디의 범주의voting값으로 예측 회귀 트리 끝마디의 ഥ 𝐲로 예측 Node1 y11 = 10 y12 = 12 y13 = 13 y14 = 8 y15 = 7 ത 𝑦 = 10 Node2 y21 = 20 y22 = 24 y23 = 26 y24 = 16 y25 = 14 ത 𝑦 = 20 Yes: 90 No: 10 Yes: 34 No: 66 yes no 32 해석 및 예측
  • 33.
    단점 장점 1. 해석의 용이성 -나무구조에 의해서 모형이 표현되기 때문에 해석이 쉽다. - 새로운 자료에 모형을 적합 시키기 쉽다. - 어떤 입력변수가 중요한지 파악이 쉽다. 2. 교호작용 효과의 해석 - 두 개 이상의 변수가 결합하여 목표변수에 어떠한 영향을 주는지 알기 쉽다. 3. 비모수적 모형 - 선형성, 정규성, 등분산성의 가정이 필요하지 않다. - 단지 순위만 분석에 영향을 주므로 이상치에 민감하지 않다. 1. 비연속성 - 연속형 변수를 비연속적인 값으로 취급하여 예측오류가 클 가능성이 있다. 2. 선형성 또는 주효과의 결여 - 선형 또는 주효과 모형에서와 같은 결과를 얻을 수 없다. 3. 비안정성 - 분석용 자료에만 의존하므로 새로운 자료의 예측에 불안정하다. 33
  • 34.
    정리 Tree는 해석이 용이하고,의사결정 방법이 인간의 의사결정 방법과 유사하지만, 예측력이 많이 떨어지고, bias-variance 문제가 발생한다. 이를 해결하기 위해! Tree를 여러 개 생성하고 결합하는 Ensemble (bagging, boosting, Random Forest)을 사용하여 Tree의 예측력을 높인다. 34
  • 35.
  • 36.
    Ensemble 여러 개의 분류,회귀 모형을 조합하여 예측의 정확도를 높이는 방법 Bias & variance Trade off를 해결해 error를 낮추는 것이 목적 배깅(Bagging) / 부스팅(Boosting) / 스태킹(Stacking) 36
  • 37.
    앙상블을 왜 사용할까? 학습에서의오류 1. Underfitting(낮은 bias) 2. Overfitting(높은 Variance) 특히 배깅은 각 샘플에서 나타난 결과를 일종의 중간값으로 맞추어 주기 때문에 overfitting을 피할 수 있다. 범주형일 경우, Voting으로 집계 연속형일 경우, Average로 집계 앙상블 기법을 통해 오류를 최소화! 37
  • 38.
  • 39.
    부스팅 Boosting 배깅 Bootstrap AGGregatING (Bagging) 여러 번의샘플을 뽑아 각 모델을 학습시켜 결과를 집계(Aggregating)하는 방법 Random Forest 약한 학습 결과를 합쳐 강한 학습 결과를 만드는 방법 AdaBoost / XGBoost GBM / Light GBM 39
  • 40.
  • 41.
    Bagging Bagging: Bootstrap aggregating의준말. (Bootstrap: 데이터에서 일부를 샘플링하는 것) - 원 데이터 집합으로부터 크기가 같은 표본을 여러 번 단순 임의 복원 추출하여 각 표본에 대해 분류기를 생성한 후 그 결과를 앙상블 하는 방법 - 반복 추출 방법을 사용하기 때문에 같은 데이터가 한 표본에 여러 번 추출 될 수도, 어떤 데이터는 추출되지 않을 수도 있다. - 하나의 학습 데이터에 overfitting 되어 테스트 데이터에서 성능이 낮을 경우 즉, high variance일 경우를 여러 개의 학습 데이터를 만들어 결합함으로써 low variance로 변화시켜 예측 성능을 향상시킨다. 41
  • 42.
    1. n번 단순임의 복원 추출 Bagging 42 A B C D Train data A A A B B D D D C C C C . . . Bootstrap sample1 Bootstrap sample2 Bootstrap sample3
  • 43.
    2. 여러 개의단일 모델 생성 Bagging 43 A A A B B D D D C C C C . . . training training training model1 model2 model3 . . . 범주형: voting 연속형: averaging
  • 44.
  • 45.
  • 46.
    Bagging > Variance를 낮추기좋다. 서로 다른 여러 개의 모델들의 결과들을 모두 고려하여 최종 결과를 내기 때문에 하나의 trainset에 너무 치중된 상태에서 train이 되는 경우(overfitting)를 피할 수 있다. 동시에 모델의 높은 정확도도 유지할 수 있다. >> 과적합 우려가 큰 (=variance가 큰) 머신러닝 기법들에 적용하기 좋은 앙상블 방법이다. 46
  • 47.
    Bagging 랜덤 포레스트(Random Forest) >의사결정나무에 배깅을 적용한 모형 = Data Bagging + Feature Bagging + Decision Tree Data Bagging > 데이터를 임의 단순 복원 추출 시행(일반적인 배깅) Feature Bagging(특성 배깅) > 변수를 임의 단순 복원 추출 (무작위로 선택된 특성을 이용=임의 노드 최적화) Decision Tree > 의사결정 나무(CART) 47 Random Forest
  • 48.
    Bagging 48 Random Forest =Data Bagging + Feature Bagging + Decision Tree 온도 습도 풍속 비 여부 A 15 60 15 1 B 21 10 1 1 C 3 70 5 0 D 7 2 30 0 온도 습도 비 여부 A 15 60 1 A 15 60 1 C 3 70 0 A 15 60 1 습도 풍속 비 여부 D 2 30 0 B 10 1 1 C 70 5 0 C 70 5 0 Tree1 Tree2 Tree correlation(모두 동일한 변수를 가져왔을 때 생기는 문제)이 높아지는 것을 방지하기 위해 feature bagging 실행
  • 49.
    Bagging Random Forest 성능평가 OOB(Out-Of-Bag)error > 부트스트랩 샘플링 과정에서 추출되지 않은 데이터들을 따로 랜덤포레스트로 학습시켜 나온 결과 > OOB 샘플들은 주로 평가용 데이터에서의 오분류율을 예측하는 용도 및 변수 중요도를 추정하는 용도로 많이 이용된다. 49
  • 50.
    Bagging Random Forest RandomForest 중요 특징: 변수 중요도 - 데이터 분석 시 가장 중요한 issue 중 하나는 변수 선택! - Feature bagging을 적용하는 Random Forest는 각 변수들의 중요성에 순위를 매길 수 있다. - Random Forest 구성 과정에서 각 feature에 대한 OOB-오차(Out-Of-Bag error)가 구해진다. (OOB: Bootstrap을 통한 임의 중복 추출 시 각 feature에 대한 test data) - 분류의 경우, 해당 변수로 부터 분할이 일어날 때 불순도의 감소가 얼마나 일어나는지에 따라 변수 중요도 결정 - 회귀의 경우, 잔차제곱합을 통해 변수 중요도 측정 50
  • 51.
  • 52.
    Boosting Boosting Bootstrap 샘플링 이후, 분류결과를 이용하여 분류가 잘못된 데이터에 더 큰 가중치를 부여하여 표본을 추출하는 방법 > Bagging은 병렬로 학습하는 반면, Boosting은 순차적으로 학습 > 학습이 끝나면 나온 결과에 따라 가중치 재분배 > 오답에 대해 높은 가중치를 부여하고 정답에 대해 낮은 가중치를 부여하여 오답에 더욱 집중할 수 있도록 한다. 52
  • 53.
  • 54.
    Boosting 54 알고리즘 특징 비고 AdaBoost- 오분류에 대해 가중치 부여 2003 GBM - Loss Function의 gradient를 통해 오답에 가중치 부여 2007 XGBoost - GBM 대비 성능 향상 - 시스템 자원 효율적 활용(CPU, Mem) - Kaggle을 통한 성능 검증 2014 Light GBM - XGBoost 대비 성능 향상 및 자원소모 최소화 - XGBoost가 처리하지 못하는 대용량 데이터 학습 가능 - Approximates the split(근사치의 분할)을 통한 성능 향상 2016
  • 55.
    Boosting AdaBoost 0. 배깅과동일하게 샘플 데이터 추출 1. 하나의 모형 학습(Box1) 2. 학습 결과로 예측하여 틀린 사례에 큰 가중치 부여하고 다시 학습(Box2) 3. 이 과정을 반복(Box3)하여 학습 결과를 합친다.(Box4) > 잡음이 많은 데이터와 이상점에 취약하다. AdaBoost 55
  • 56.
    1. 1회 복원추출후 트리 모델 생성 AdaBoost 56 A B C D Train data A C D Tree 1 Bagging과 동일 A
  • 57.
    2. 가중치 업데이트 AdaBoost 57 B C D A B C D Traindata Train_Data로 test를 한 후, 오분류된 데이터들이 추출될 확률을 높인 후 1번 과정을 다시 시행 가중치 A 1 4 B 1 4 C 1 4 D 1 4 업데이트된 가중치 A 1 4 ∗ exp(−𝑎)/(𝐴 + 𝐵 + 𝐶 + 𝐷) B 1 4 ∗ exp(𝑎)/(𝐴 + 𝐵 + 𝐶 + 𝐷) C 1 4 ∗ exp(−𝑎)/(𝐴 + 𝐵 + 𝐶 + 𝐷) D 1 4 ∗ exp(−𝑎)/(𝐴 + 𝐵 + 𝐶 + 𝐷) B Tree 2 #. e(에러율): 오류데이터 가중치 합 / 전체 데이터 가중치 합 #. a(신뢰도): 1 2 ∗ ln( 1−𝑒 𝑒 ) B만 오분류된 상태
  • 58.
    3. 위 과정반복 AdaBoost 58 에러율이 0이 될 때까지 혹은 트리 모델 수가 일정한 수에 도달할 때까지 위 과정들을 계속 반복 . . . A B C D Train data D C D B B C D B C Tree 1 Tree 2 Tree 3 A A A
  • 59.
    4. 신뢰도(a)를 곱하여voting AdaBoost 59 Tree 1 Predict*a Tree 2 Predict*a Tree 3 Predict*a . . . . . . + + =
  • 60.
  • 61.
    Boosting GBM GBM(Gradient Boosting)= 경사 부스팅 > 이전의 학습 결과와 실제의 차이를 학습하는 방식 > 가중치 계산 방식에서 Gradient Descent를 적용 두번째 학습 결과 f2가 첫번째 예측 오차를 학습 첫번째 학습 결과 f1 학습이 잘 되었다면, 첫번째 학습 오차분산 Var(e1)보다 두번째 학습의 오차분산 Var(e2)가 더 줄어들게 된다. 61
  • 62.
    Boosting GBM 학습기 M에대해서 Y를 예측할 확률 > Y = M(x) + error > error = G(x) + error2 (error > error2) > error2 = H(x) + error3 (error2 > error3) > Y = M(x) + G(x) + H(x) + error3 학습기 M을 단독으로 사용했을 때보다 정확도가 높을 것이다. (error > error3) Error를 세분화 62
  • 63.
    Boosting GBM 학습기 M을단독으로 사용했을 때보다 정확도가 높을 것이다. (error > error3) Error를 세분화 63 M, G, H 각각 분류기의 성능이 다른데, 모두 같은 비중을 두고 있기 때문에 임의의 x에 대해 서로 간섭하여 오류를 높이는 결과를 가져올 수 있다. 학습기 M에 대해서 Y를 예측할 확률 > Y = M(x) + error > error = G(x) + error2 (error > error2) > error2 = H(x) + error3 (error2 > error3) > Y = M(x) + G(x) + H(x) + error3
  • 64.
    Boosting GBM 각 함수별최적의 가중치를 찾으면, 예측 정확도 향상 (Gradient Descent 알고리즘으로 최적 weight값 계산) Y = alpha * M(x) + beta * G(x) + gamma * H(x) + error3 64
  • 65.
    Boosting GBM 가중치 부여방식? > 초기 데이터 가중치(D) = 1/n (n: 전체 학습 데이터 개수) > 오류(e): 오류데이터 / 전체 학습 데이터 > Weak model의 함수: h(t) (=모델의 예측값) > 가중치 업데이트(D) > 모델의 가중치(a) (=learning rate역할) 65
  • 66.
    Boosting XGBoost - GBM+ 분산/병렬 처리 - Split 지점을 고려할 때 일부를 보고 결정 - Sparsity Awareness가 가능 - Binary classification / Multiclass classification / Regression / Learning to Rank XGBoost (eXtreme Gradient Boosting) > 목적함수를 정의하고 이를 최소화 하는 값을 찾아 가중치를 업그레이드 > 지도학습으로 변수(x)를 학습하여 정답(y)을 예측 66
  • 67.
    Boosting XGBoost > CPU병렬처리, 코어들이 각자 할당 받은 변수들로 제각기 가지를 쳐 나간다. > 연산시간 단축 67
  • 68.
    Boosting XGBoost > 연속형변수에서 split 지점을 고려할 때 모든 값들을 살펴보고 결정하기 보단 일부분만을 보고 결정을 한다. ID 국어 수학 1 100 90 2 95 80 3 75 90 4 20 55 일부 후보군만 보고 split 지점 결정 68
  • 69.
    Boosting XGBoost > SparsityAwareness가 가능 > Zero 데이터를 건너뛰면서 학습이 가능하다. > Input을 dummy화 하면 속도가 상승! ID 과목 1 국어 2 수학 3 영어 4 과학 ID 국어 수학 영어 과학 1 1 0 0 0 2 0 1 0 0 3 0 0 1 0 4 0 0 0 1 69
  • 70.
    Boosting Light GBM 70 LightGBM > Decision Tree 알고리즘 기반의 GBM 프레임워크 (속도, 성능 향상) > Ranking, Classification등의 문제에 활용 다른 tree 알고리즘과의 차이점? - Leaf-wise로 tree를 성장(수직 방향) - 최대 delta loss의 leaf를 성장 즉, 동일한 leaf를 성장시킬 때, leaf-wise가 loss를 더 줄일 수 있다. https://www.slideshare.net/freepsw/boosting-bagging-vs-boosting
  • 71.
    Boosting Light GBM 71 Leaf-wise(LightGBM) > 가장 loss변화가 큰 노드에서 데이터를 분할 > 학습 데이터가 많은 경우 뛰어난 성능 > 수직 성장 Level-wise(XGBoost, Random Forest) > 각 노드는 root 노드와 가까운 노드를 우선 순회 > 수평 성장
  • 72.
    Boosting Light GBM 72 왜Light GBM이 인기가 있을까? > 대량의 데이터를 병렬로 빠르게 학습이 가능하다.(Low memory, GPU 활용가능) > 예측 정확도가 더 높다. (Leaf-wise tree의 장점: 과적합에 민감) 특징 > XGBoost의 2~10배 (동일한 파라미터로 설정)빠르다. > Leaf-wise tree는 overfitting에 민감하여, 대량의 데이터 학습에 적합하다. (적어도 10,000개 이상의 행이 있는 데이터에 적합하다.)
  • 73.
    Stacking “Two heads arebetter than one” = Meta modeling 여러 모델들의 결과값을 averaging, voting하여 새로운 결과값 생성 여러 모델들의 결과값을 새로운 변수로 데이터셋 생성 (이후 다시 모델 학습) 73
  • 74.
    Stacking > 여러 모델들의결과값을 averaging, voting하여 새로운 결과값 생성 종속변수: 범주형 - Predict 값 중 확률 값들을 평균내 최종 예측 값으로 사용 - 예측 값 자체를 voting하여 최종 예측 값으로 사용 종속변수: 연속형 - 예측 값 자체를 averaging하여 최종 예측 값으로 사용 74
  • 75.
    Stacking > 여러 모델들의결과값을 새로운 변수로 데이터셋 생성 (이후 다시 모델 학습) 종속변수: 범주형 - Predict 값 중 확률 값들을 새로운 변수로 사용 - 예측 값 자체를 새로운 변수로 사용 종속변수: 연속형 - 예측 값 자체를 새로운 변수로 사용 75
  • 76.
  • 77.
    Stacking Train Test predict Model 1 Train Test feature1 새로운 변수로데이터셋 생성 77 Train Test predict Model 2 feature2
  • 78.