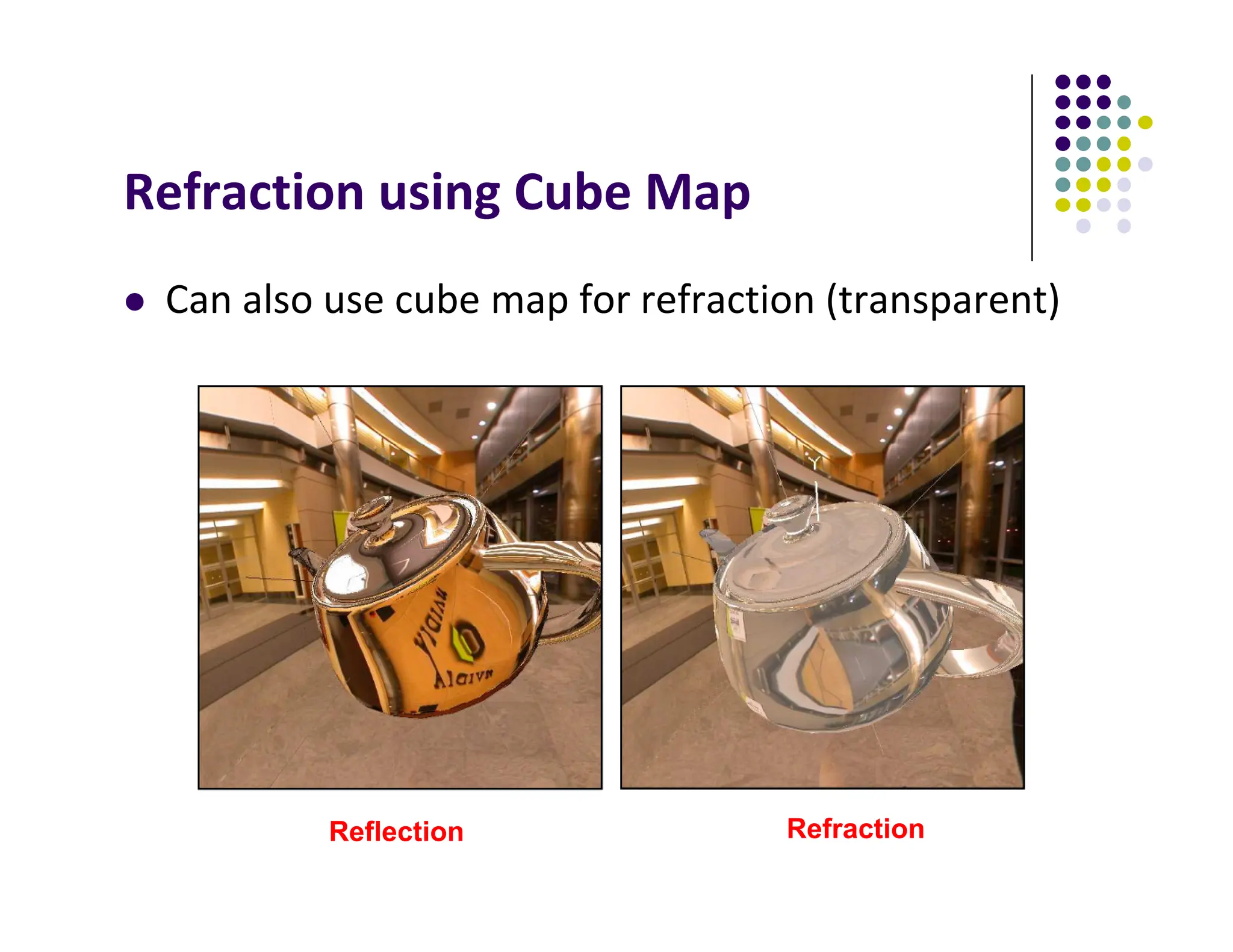
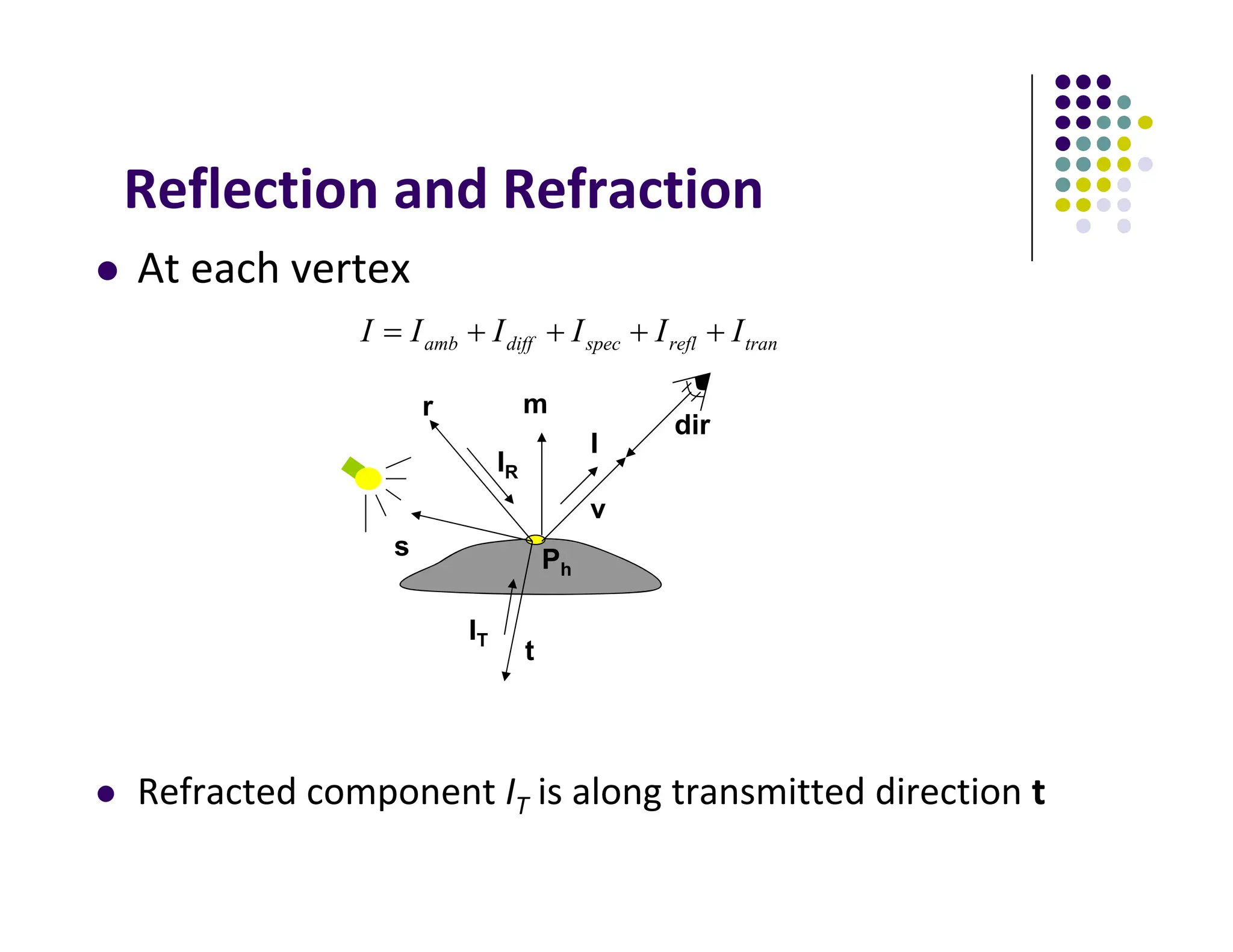
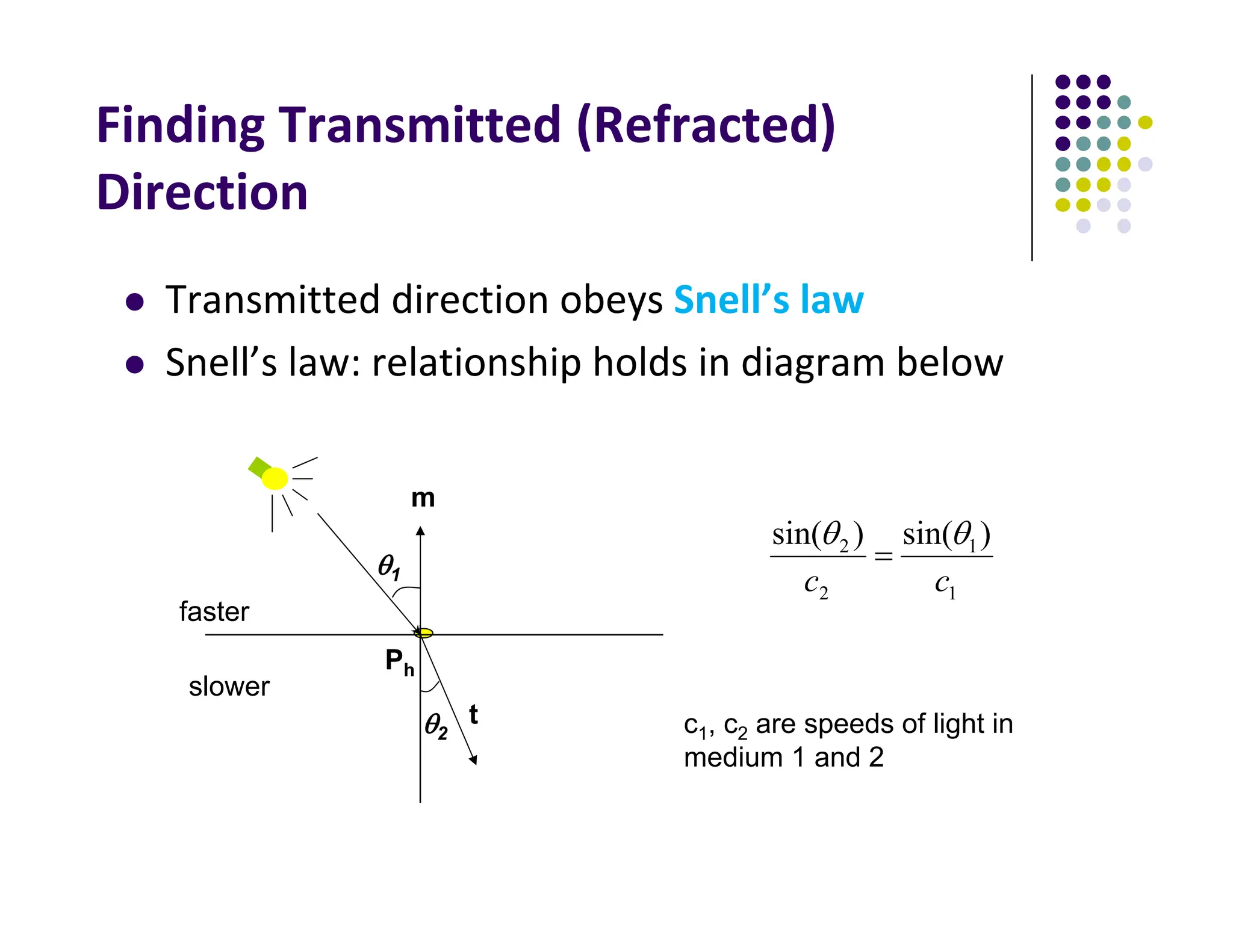
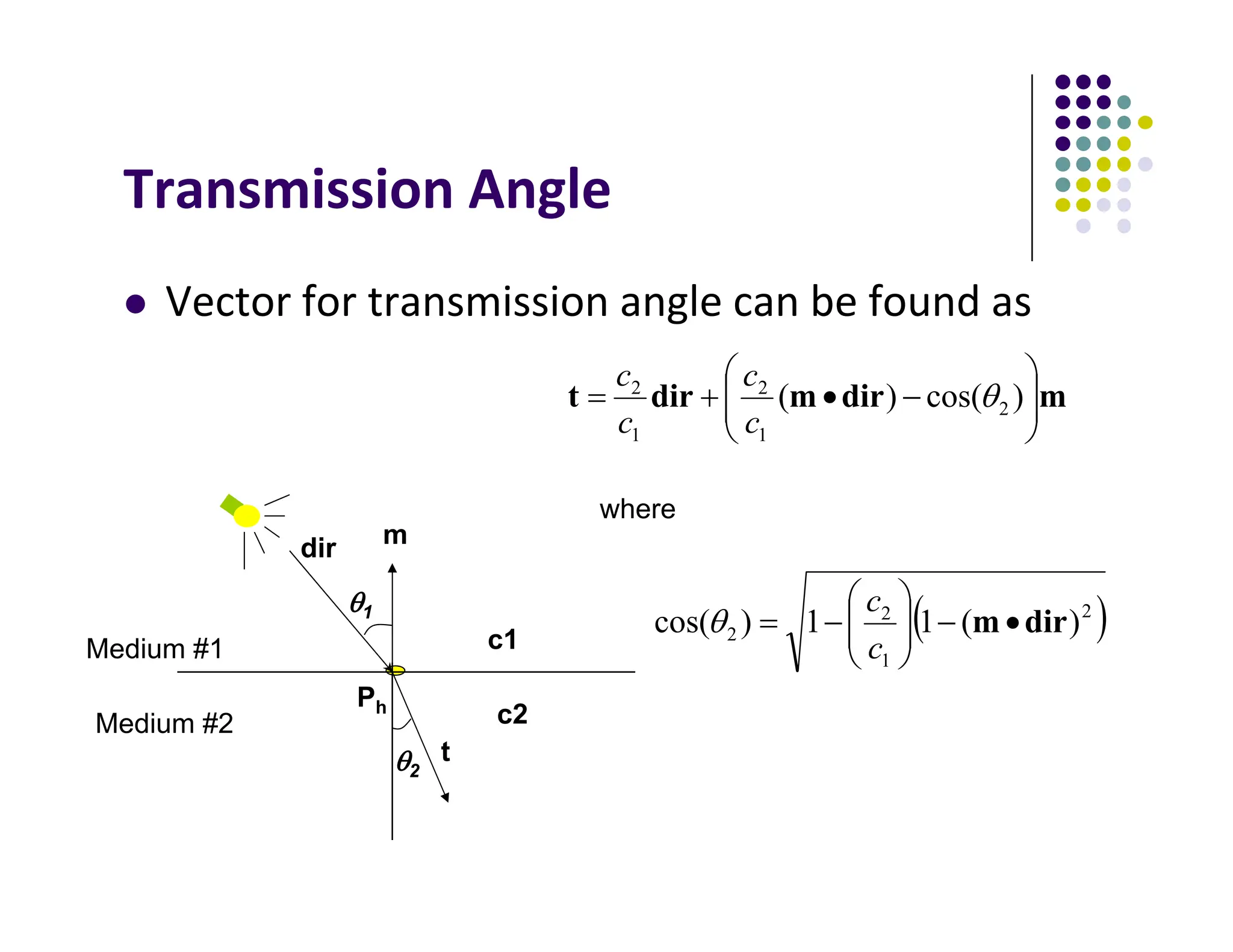
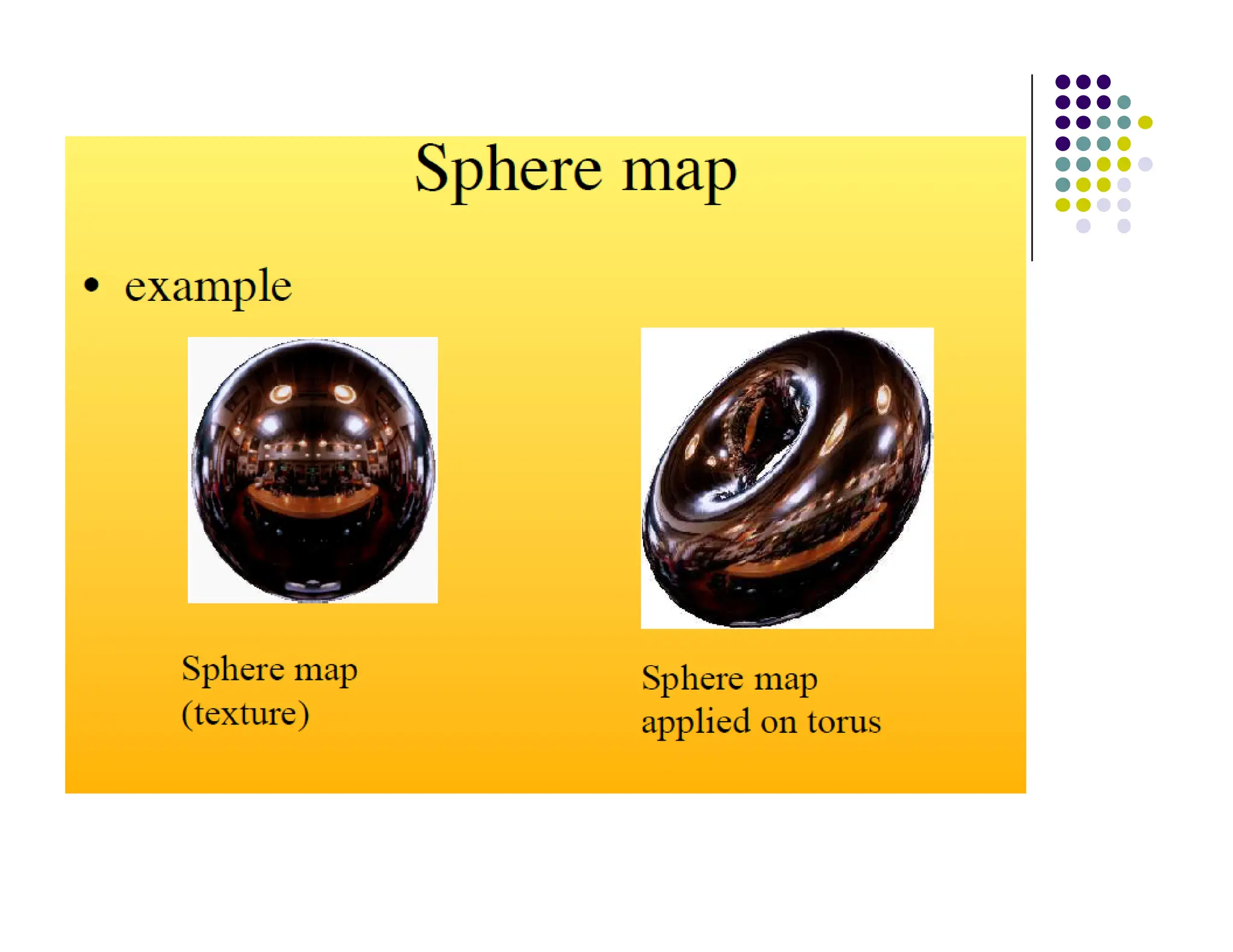
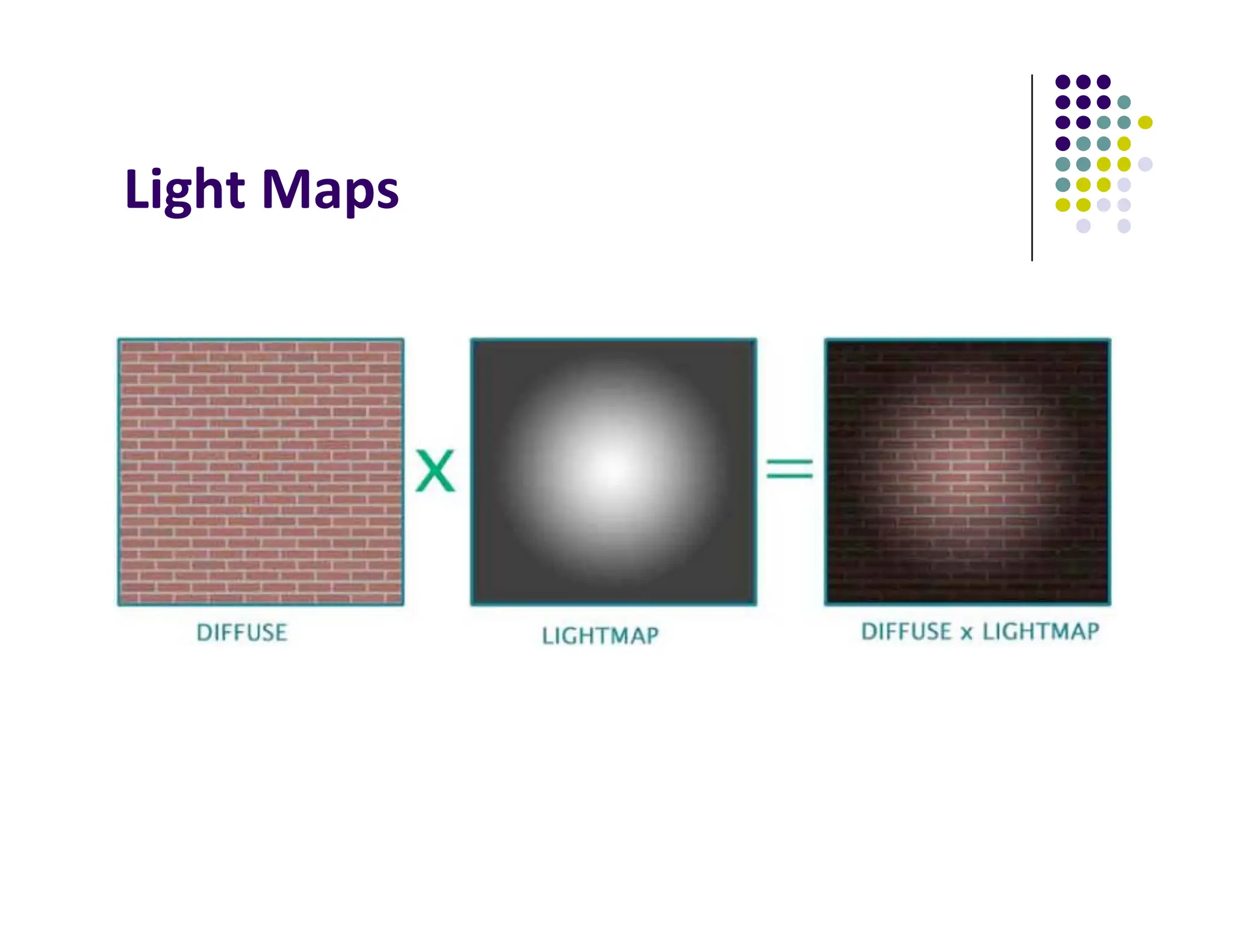
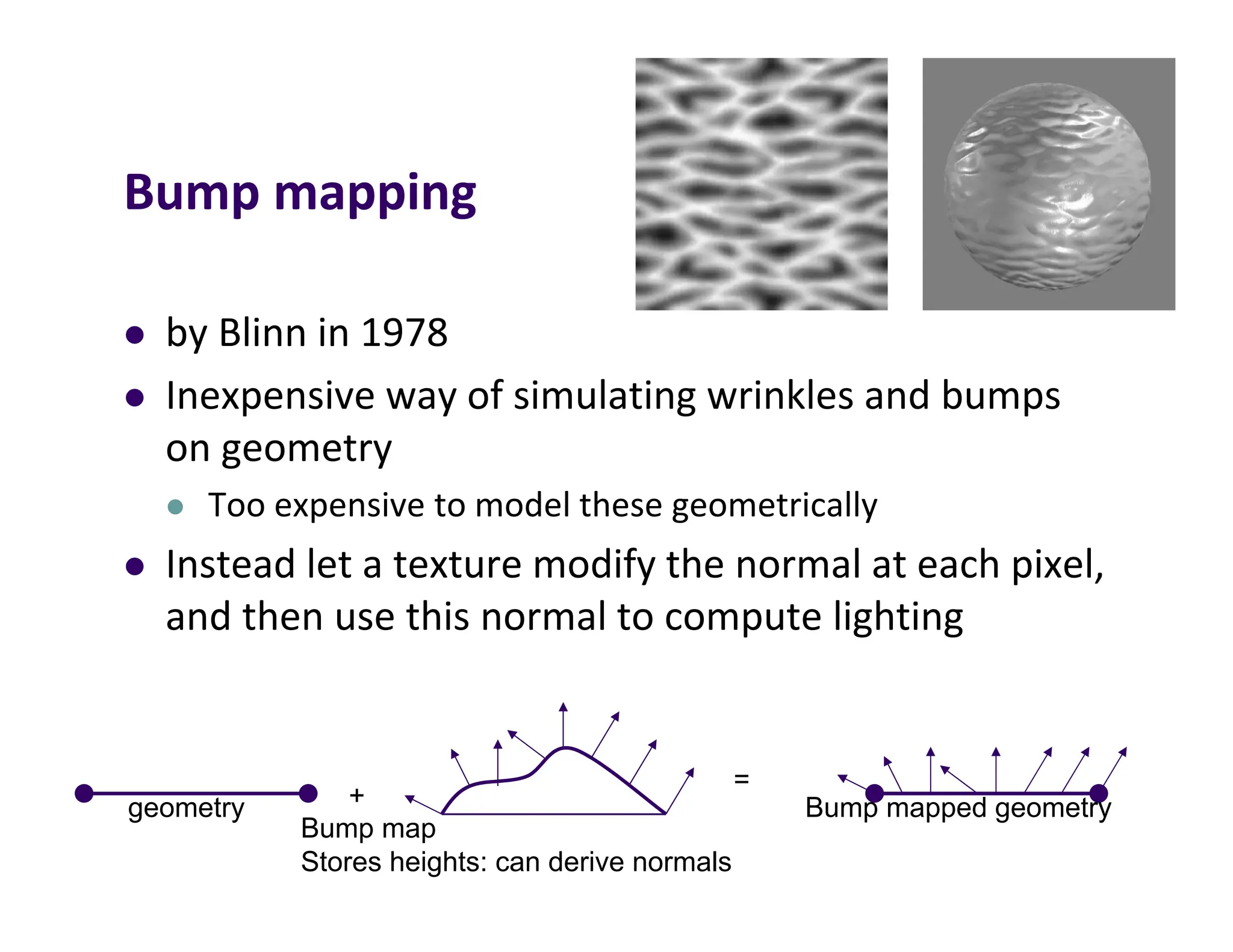
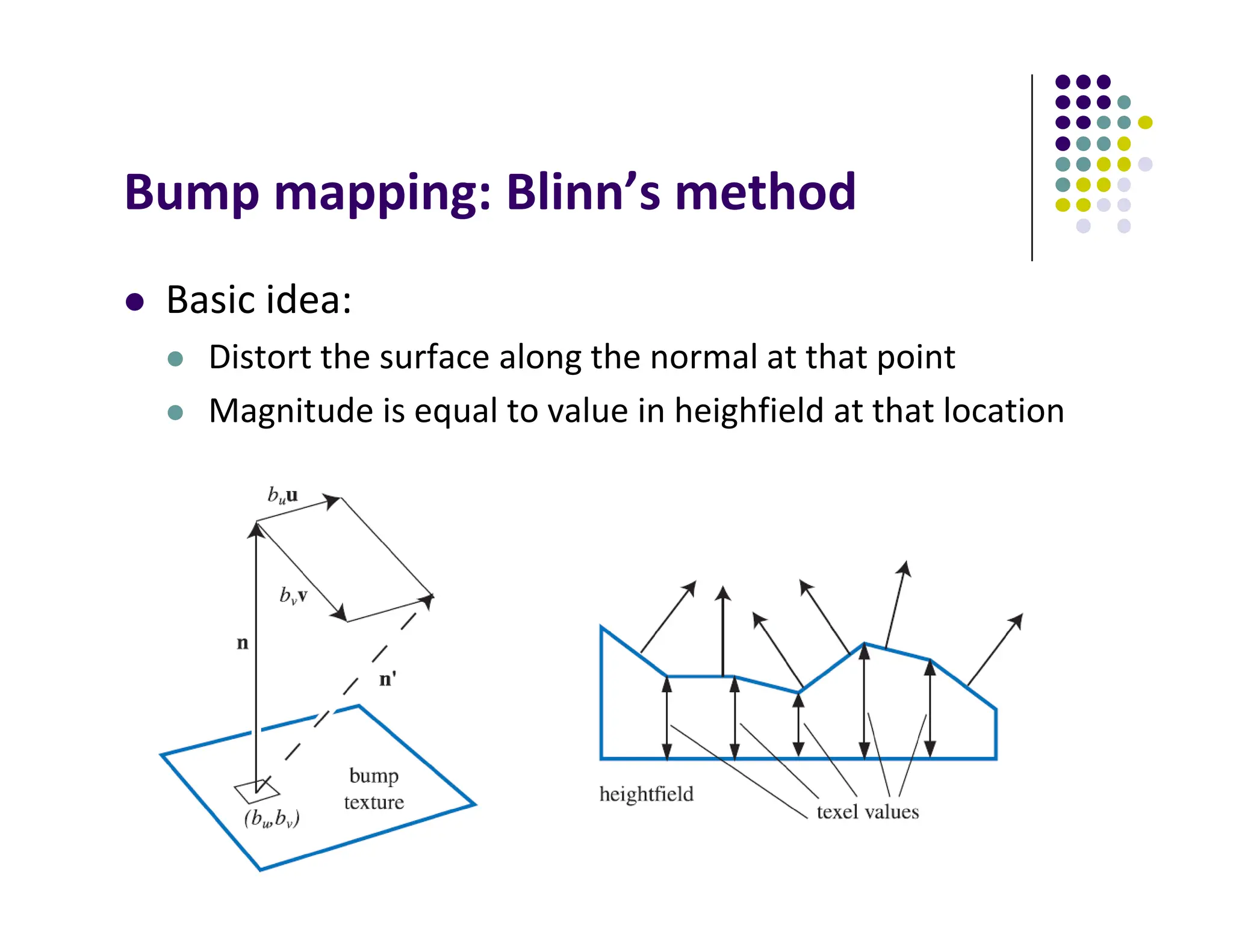
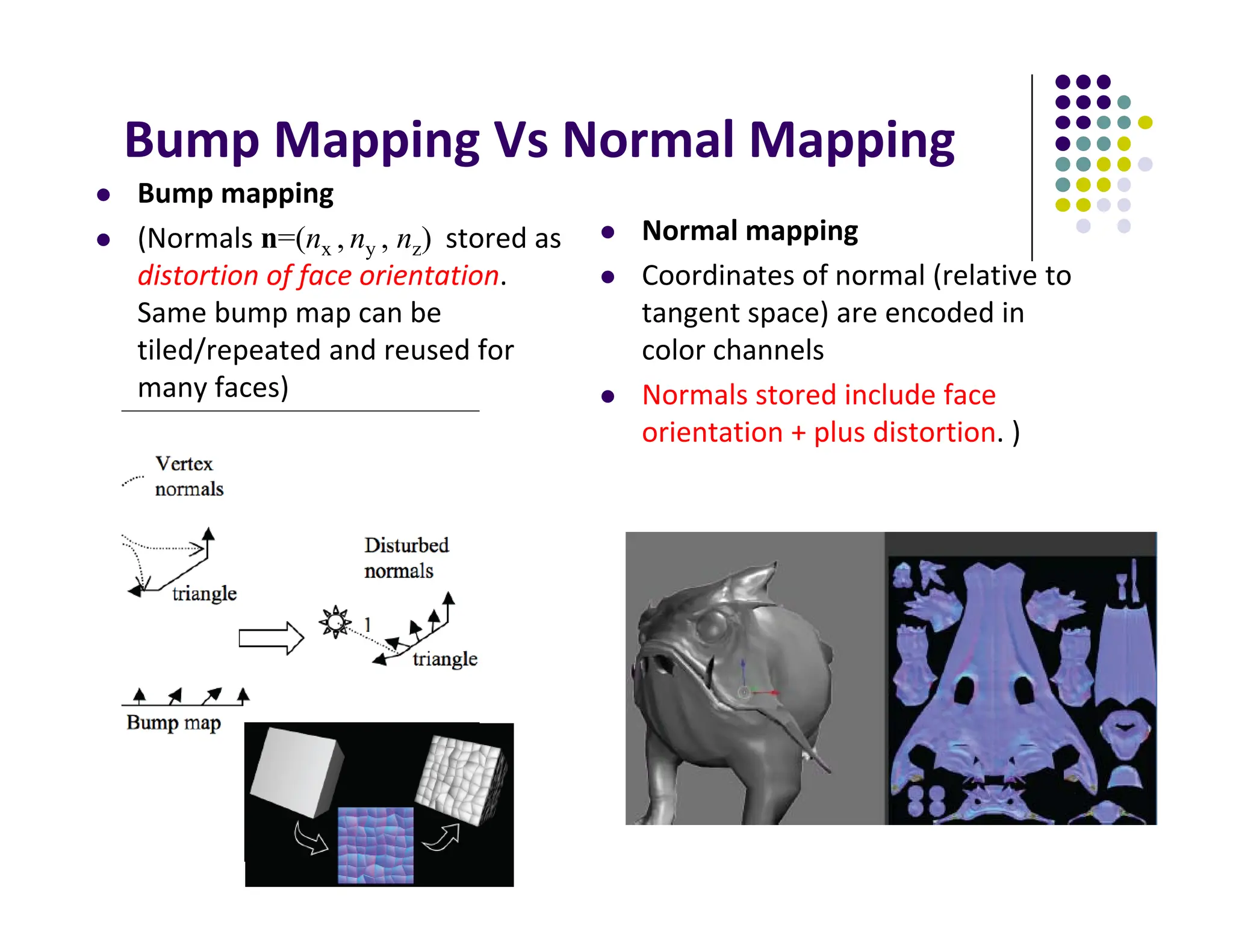
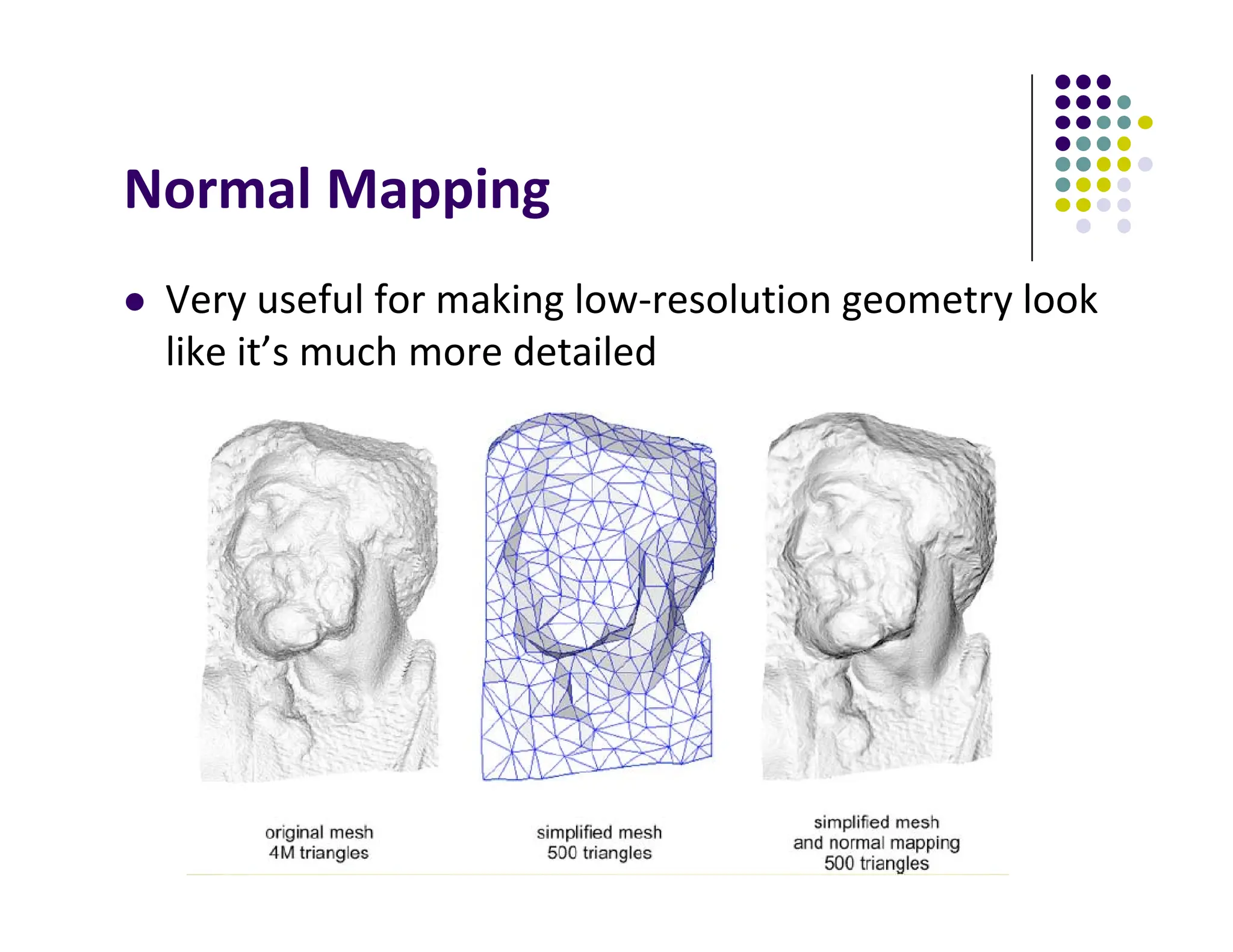
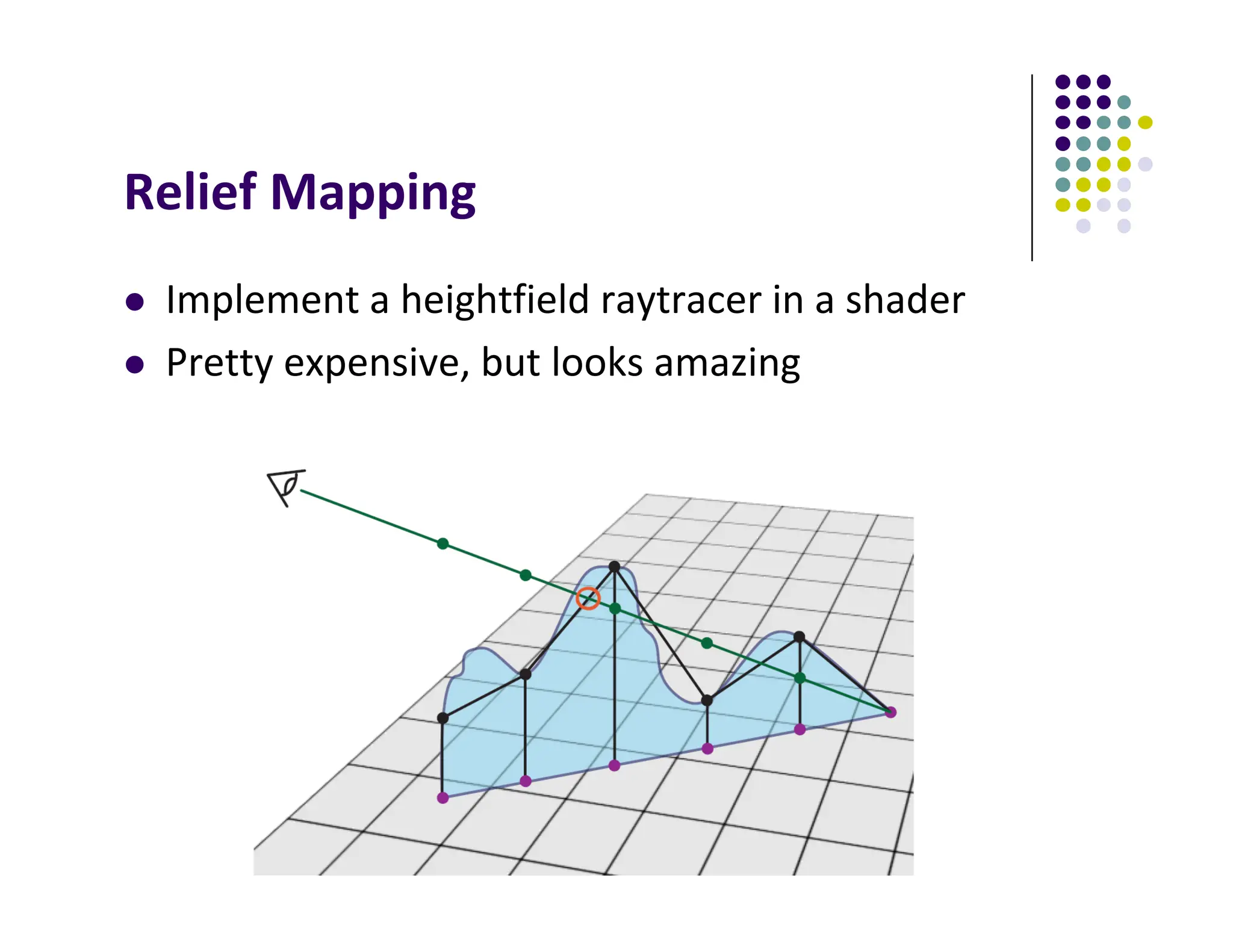
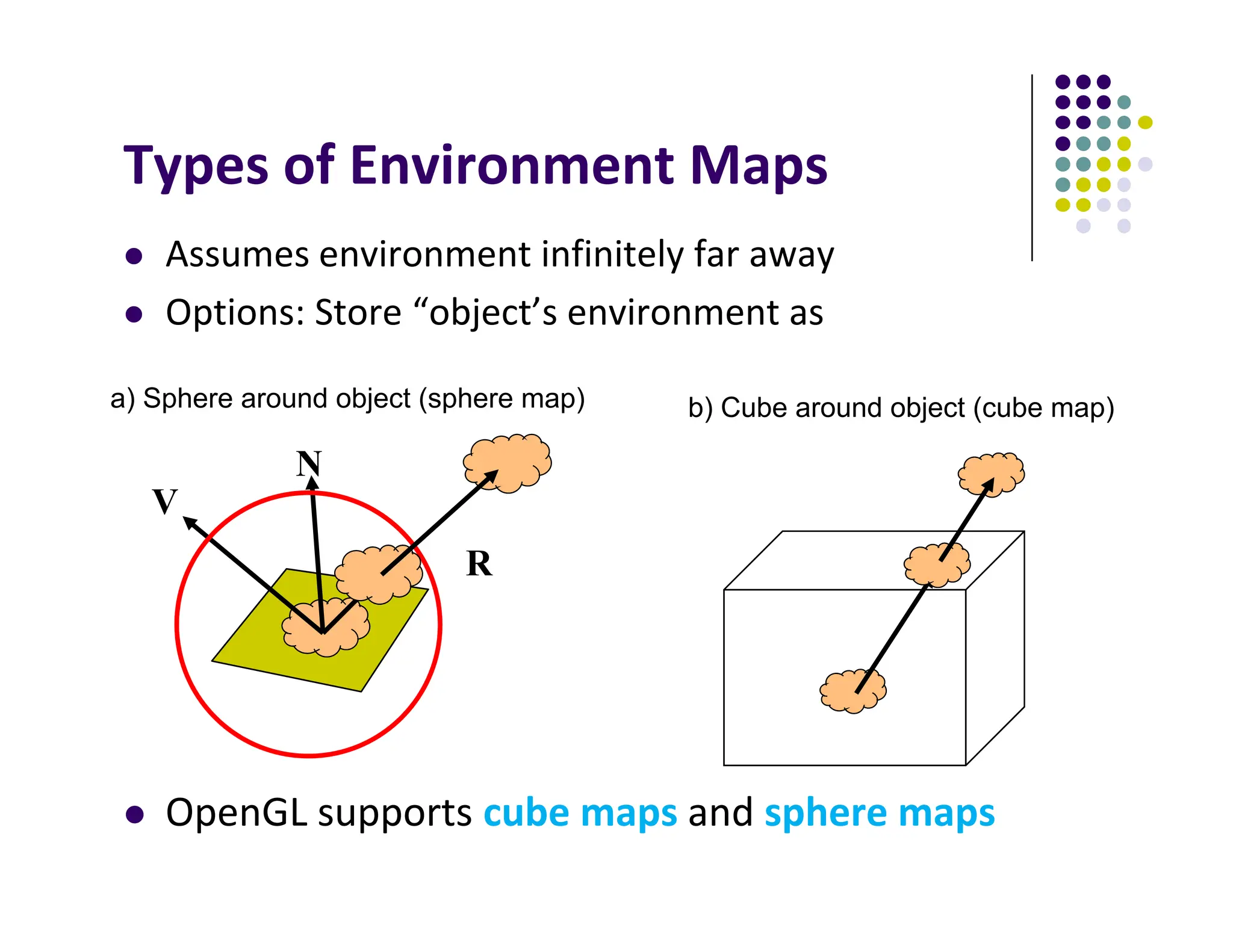
The document discusses environment mapping techniques in computer graphics, focusing on creating reflections and refractions without ray tracing by using cube and sphere maps. It explains how these maps are defined, how to calculate reflection and refraction vectors, and the implementation of these techniques in OpenGL. Additionally, it covers various texturing methods such as bump mapping, normal mapping, displacement mapping, and parallax mapping to enhance realism in 3D graphics.

1. Computer Graphics (CS 543)
Lecture 9 (Part 1): Environment
Mapping (Reflections and Refractions)
Prof Emmanuel Agu
(Adapted from slides by Ed Angel)
Computer Science Dept.
Worcester Polytechnic Institute (WPI)

2. Environment Mapping
 Used to create appearance of reflective and
refractive surfaces without ray tracing which
requires global calculations

4.  Assumes environment infinitely far away
 Options: Store “object’s environment as
 OpenGL supports cube maps and sphere maps
Types of Environment Maps
V
N
R
b) Cube around object (cube map)
a) Sphere around object (sphere map)

5. Cube Map
 Stores “environment” around objects as 6 sides of a
cube (1 texture)

6. 6
Forming Cube Map
 Use 6 cameras directions from scene center
 each with a 90 degree angle of view

7. x
y
z
Reflection Mapping
 Need to compute reflection vector, r
 Use r by for lookup
 OpenGL hardware supports cube maps, makes lookup easier
n
eye
r

8. 8
Indexing into Cube Map
V
R
•Compute R = 2(N∙V)N‐V
•Object at origin
•Use largest magnitude component
of R to determine face of cube
•Other 2 components give
texture coordinates

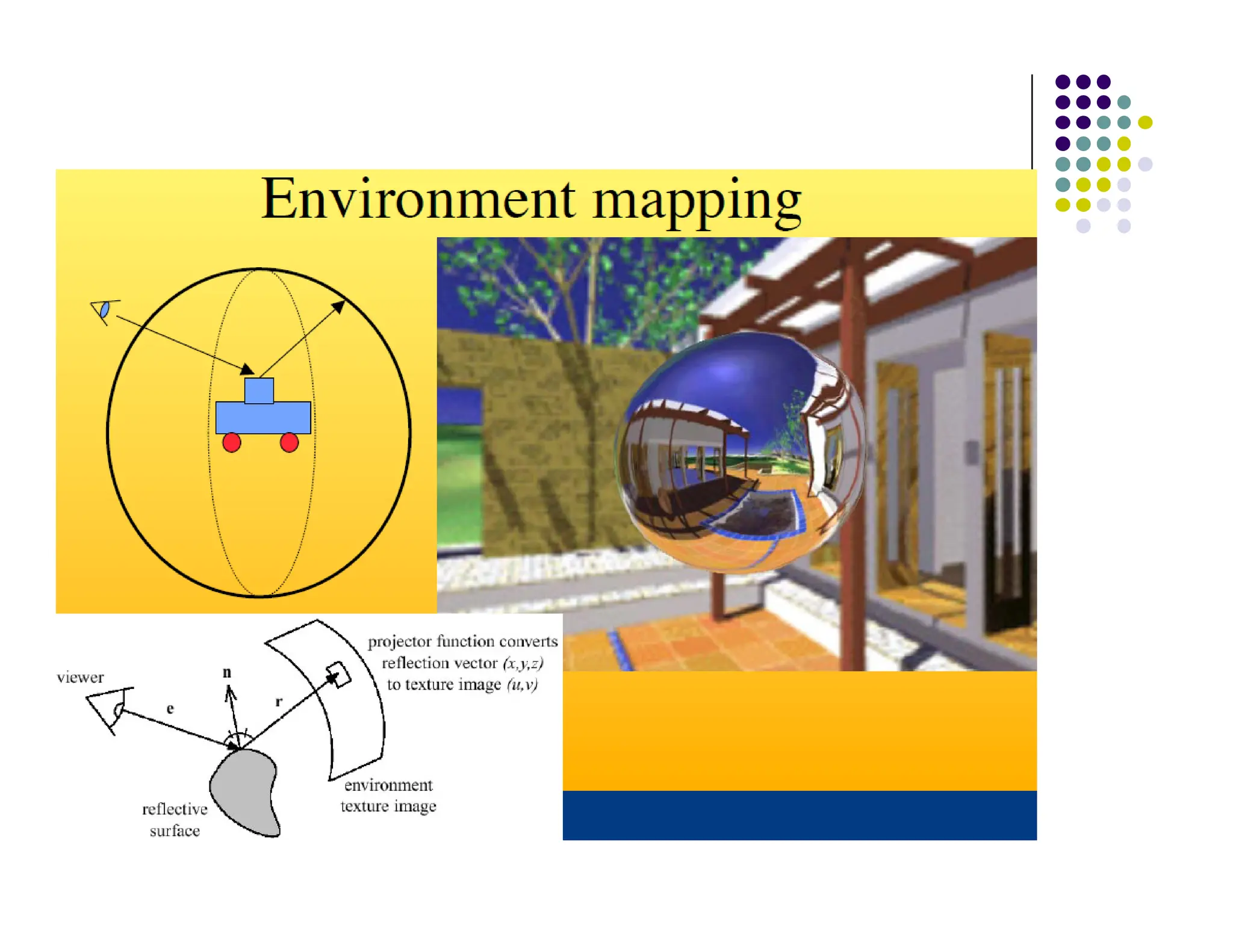
10. Example
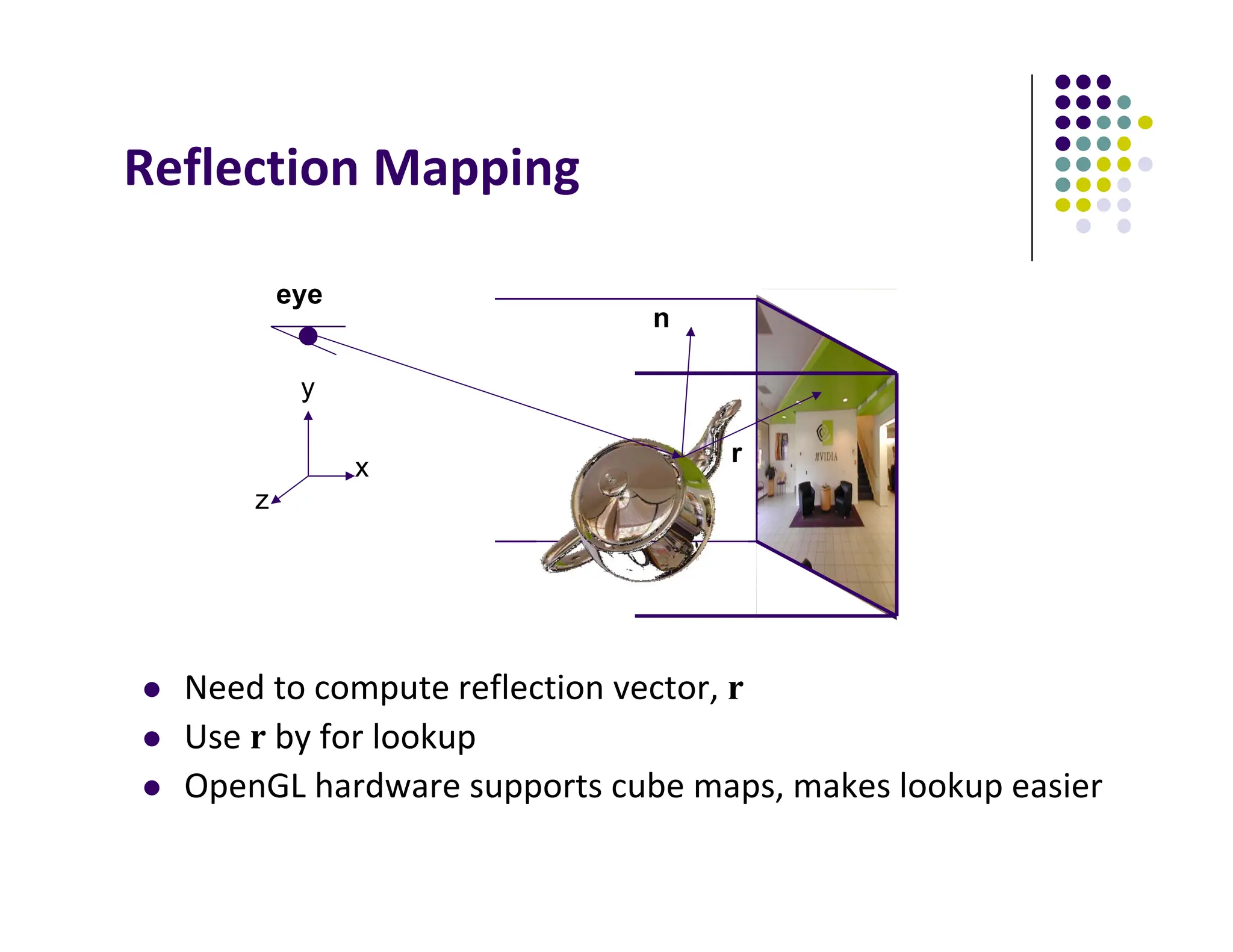
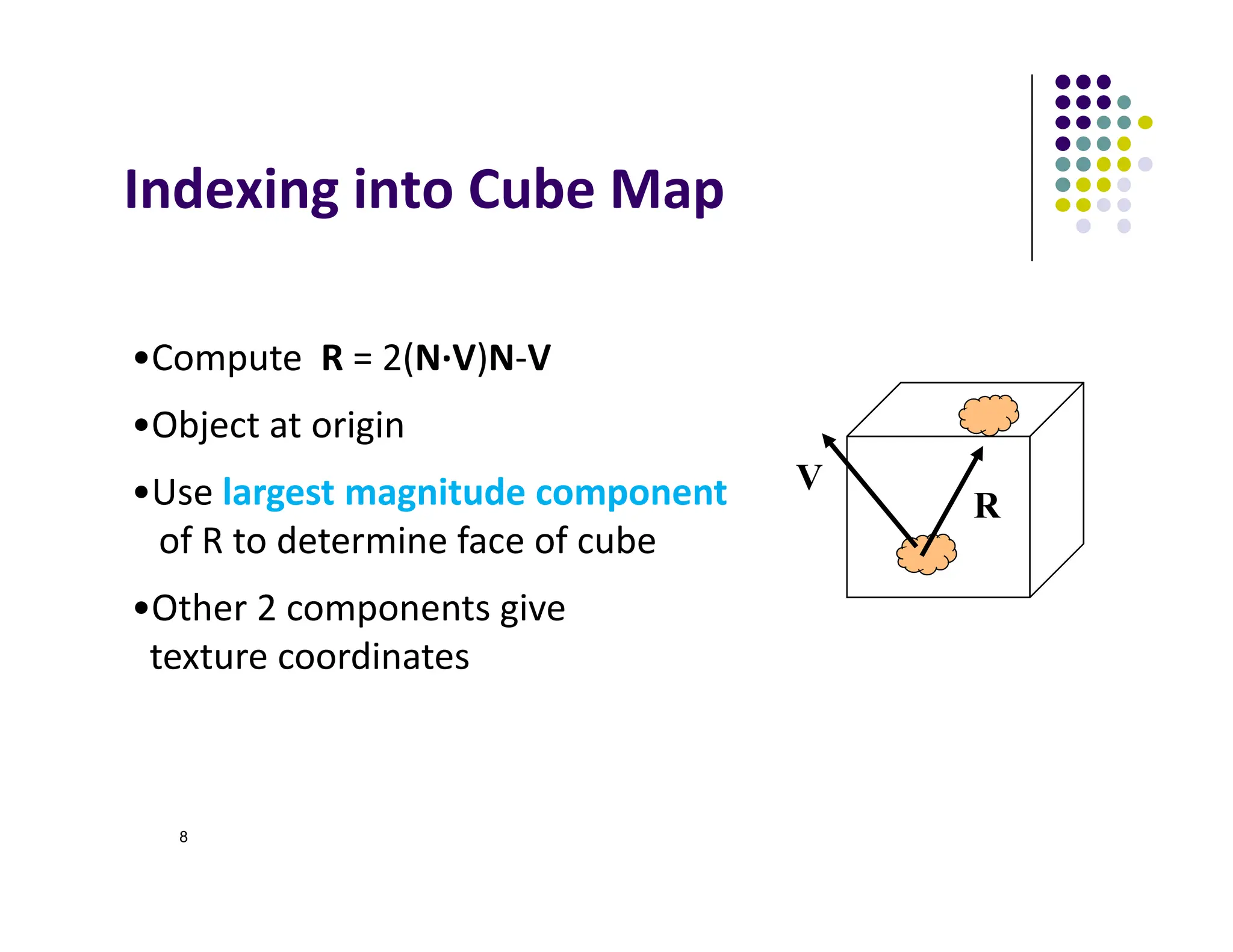
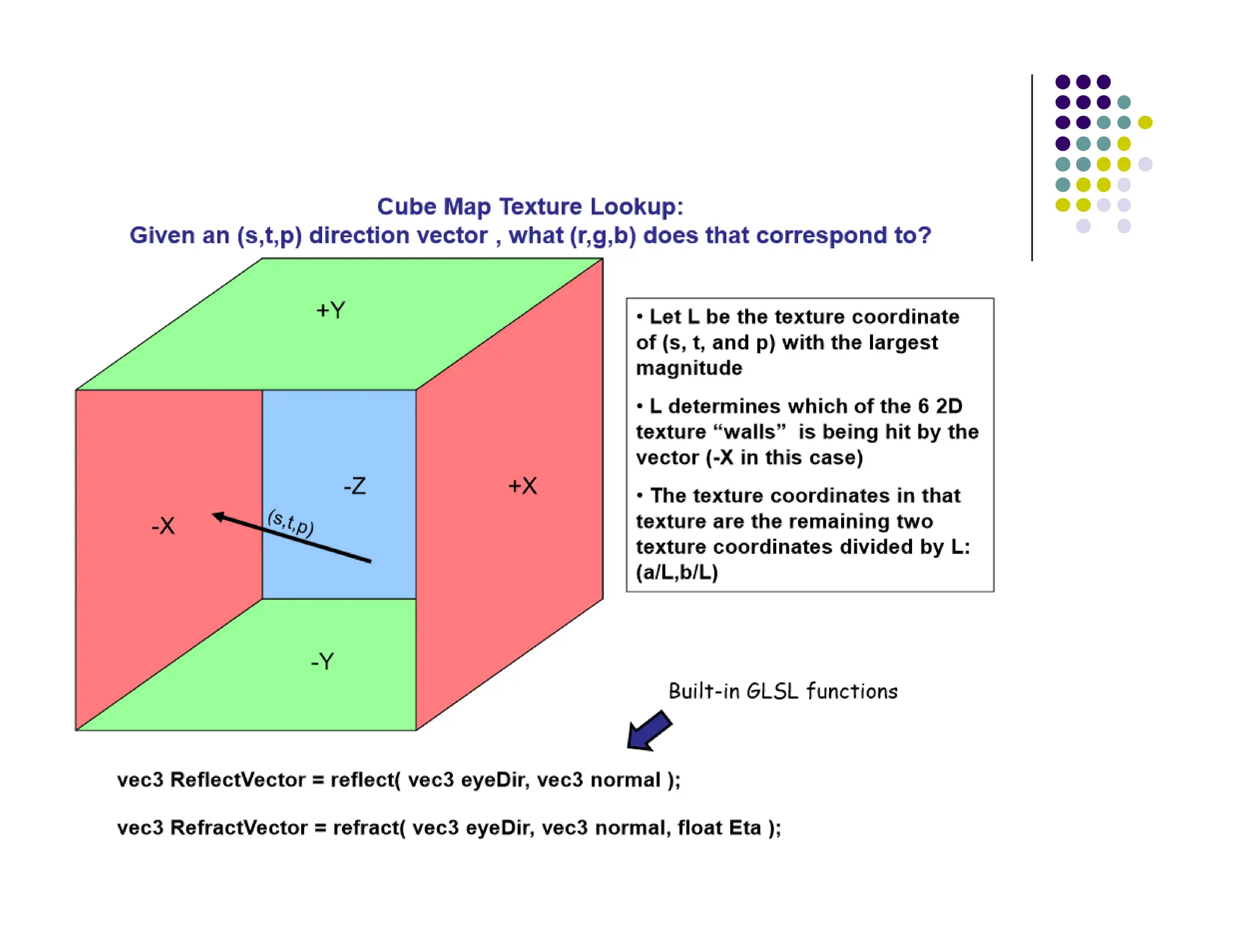
 R = (‐4, 3, ‐1)
 Same as R = (‐1, 0.75, ‐0.25)
 Use face x = ‐1 and y = 0.75, z = ‐0.25
 Not quite right since cube defined by x, y, z = ± 1
rather than [0, 1] range needed for texture
coordinates
 Remap by s = ½ + ½ y, t = ½ + ½ z
 Hence, s =0.875, t = 0.375

11. Declaring Cube Maps in OpenGL
glTextureMap2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X, level, rows,
columns, border, GL_RGBA, GL_UNSIGNED_BYTE, image1)
 Repeat similar for other 5 images (sides)
 Make 1 texture object from 6 images
 Parameters apply to all six images. E.g
glTexParameteri( GL_TEXTURE_CUBE_MAP,
GL_TEXTURE_MAP_WRAP_S, GL_REPEAT)
 Note: texture coordinates are in 3D space (s, t, r)

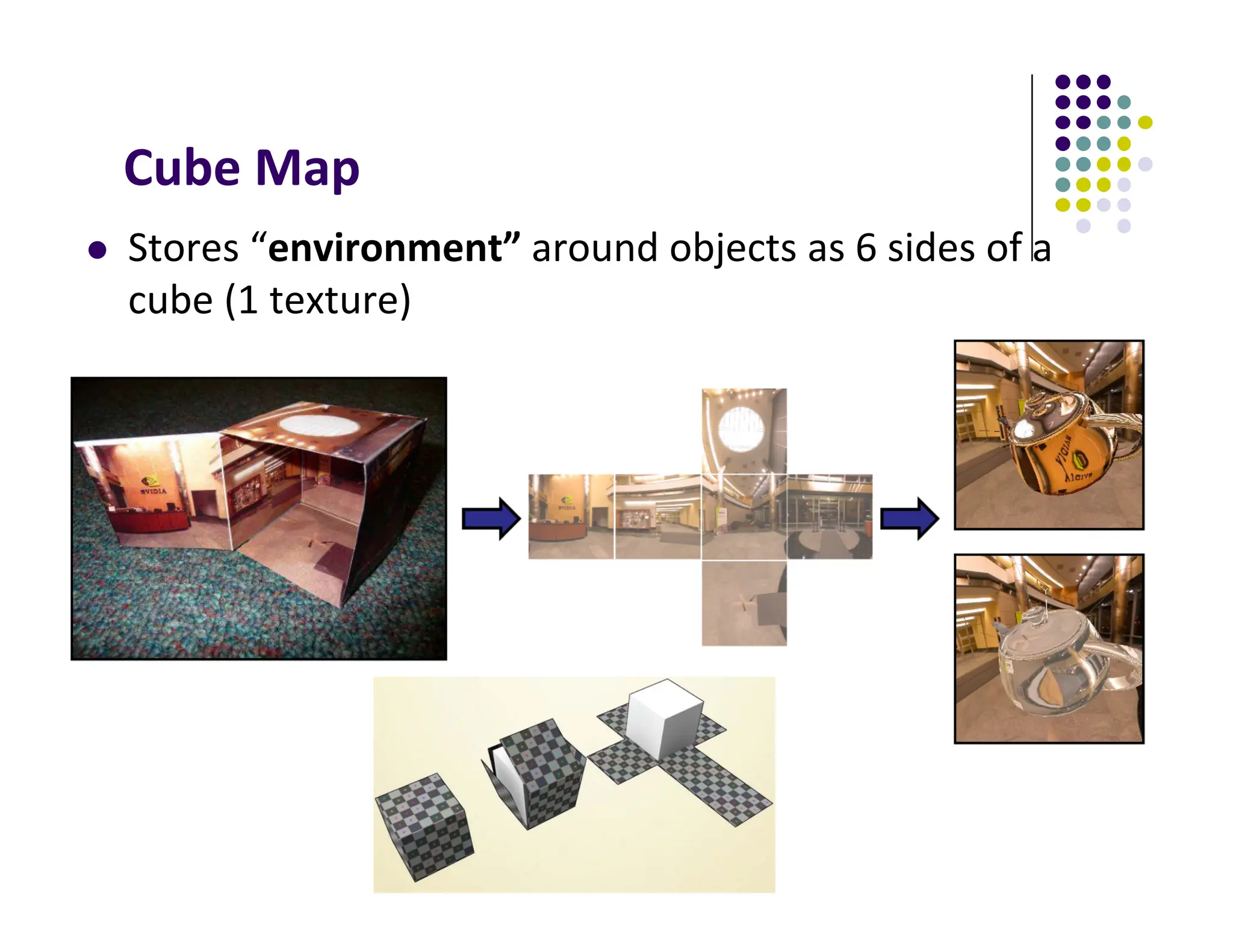
12. Cube Map Example (init)
// colors for sides of cube
GLubyte red[3] = {255, 0, 0};
GLubyte green[3] = {0, 255, 0};
GLubyte blue[3] = {0, 0, 255};
GLubyte cyan[3] = {0, 255, 255};
GLubyte magenta[3] = {255, 0, 255};
GLubyte yellow[3] = {255, 255, 0};
glEnable(GL_TEXTURE_CUBE_MAP);
// Create texture object
glGenTextures(1, tex);
glActiveTexture(GL_TEXTURE1);
glBindTexture(GL_TEXTURE_CUBE_MAP, tex[0]);
You can also just load
6 pictures of environment

13. Cube Map (init II)
glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X ,
0,3,1,1,0,GL_RGB,GL_UNSIGNED_BYTE, red);
glTexImage2D(GL_TEXTURE_CUBE_MAP_NEGATIVE_X ,
0,3,1,1,0,GL_RGB,GL_UNSIGNED_BYTE, green);
glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_Y ,
0,3,1,1,0,GL_RGB,GL_UNSIGNED_BYTE, blue);
glTexImage2D(GL_TEXTURE_CUBE_MAP_NEGATIVE_Y ,
0,3,1,1,0,GL_RGB,GL_UNSIGNED_BYTE, cyan);
glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_Z ,
0,3,1,1,0,GL_RGB,GL_UNSIGNED_BYTE, magenta);
glTexImage2D(GL_TEXTURE_CUBE_MAP_NEGATIVE_Z ,
0,3,1,1,0,GL_RGB,GL_UNSIGNED_BYTE, yellow);
glTexParameteri(GL_TEXTURE_CUBE_MAP,
GL_TEXTURE_MAG_FILTER,GL_NEAREST);
You can also just use
6 pictures of environment

14. Cube Map (init III)
GLuint texMapLocation;
GLuint tex[1];
texMapLocation = glGetUniformLocation(program, "texMap");
glUniform1i(texMapLocation, tex[0]);
Connect texture map (tex[0])
to variable texMap in fragment shader
(texture mapping done in frag shader)

15. Adding Normals
void quad(int a, int b, int c, int d)
{
static int i =0;
normal = normalize(cross(vertices[b] - vertices[a],
vertices[c] - vertices[b]));
normals[i] = normal;
points[i] = vertices[a];
i++;
// rest of data

16. Vertex Shader
16
out vec3 R;
in vec4 vPosition;
in vec4 Normal;
uniform mat4 ModelView;
uniform mat4 Projection;
void main() {
gl_Position = Projection*ModelView*vPosition;
vec4 eyePos = vPosition; // calculate view vector V
vec4 NN = ModelView*Normal; // transform normal
vec3 N =normalize(NN.xyz); // normalize normal
R = reflect(eyePos.xyz, N); // calculate reflection vector R
}

17. Fragment Shader
in vec3 R;
uniform samplerCube texMap;
void main()
{
vec4 texColor = textureCube(texMap, R); // look up texture map using R
gl_FragColor = texColor;
}

18. Refraction using Cube Map
 Can also use cube map for refraction (transparent)
Reflection Refraction

19. Reflection vs Refraction
Reflection Refraction

20. Reflection and Refraction
 At each vertex
 Refracted component IT is along transmitted direction t
tran
refl
spec
diff
amb I
I
I
I
I
I 




Ph
v
r m
s
dir
t
IR
IT
I

21. Finding Transmitted (Refracted)
Direction
 Transmitted direction obeys Snell’s law
 Snell’s law: relationship holds in diagram below
Ph
m
t
1
1
2
2 )
sin(
)
sin(
c
c



faster
slower
2
1
c1, c2 are speeds of light in
medium 1 and 2

22. Finding Transmitted Direction
 If ray goes from faster to slower medium, ray is bent
towards normal
 If ray goes from slower to faster medium, ray is bent
away from normal
 c1/c2 is important. Usually measured for medium‐to‐
vacuum. E.g water to vacuum
 Some measured relative c1/c2 are:
 Air: 99.97%
 Glass: 52.2% to 59%
 Water: 75.19%
 Sapphire: 56.50%
 Diamond: 41.33%

23. Transmission Angle
 Vector for transmission angle can be found as
Ph
m
t
m
dir
m
dir
t 










 )
cos(
)
( 2
1
2
1
2

c
c
c
c
Medium #1
Medium #2
2
1
where
dir
c2
c1
 
2
1
2
2 )
(
1
1
)
cos( dir
m 











c
c


24. Refraction Vertex Shader
out vec3 T;
in vec4 vPosition;
in vec4 Normal;
uniform mat4 ModelView;
uniform mat4 Projection;
void main() {
gl_Position = Projection*ModelView*vPosition;
vec4 eyePos = vPosition; // calculate view vector V
vec4 NN = ModelView*Normal; // transform normal
vec3 N =normalize(NN.xyz); // normalize normal
T = refract(eyePos.xyz, N, iorefr); // calculate refracted vector T
}
Was previously R = reflect(eyePos.xyz, N);

25. Refraction Fragment Shader
in vec3 T;
uniform samplerCube RefMap;
void main()
{
vec4 refractColor = textureCube(RefMap, T); // look up texture map using T
refractcolor = mix(refractcolor, WHITE, 0.3); // mix pure color with 0.3 white
gl_FragColor = texColor;
}

26. Sphere Environment Map
 Cube can be replaced by a sphere (sphere map)

27. Sphere Mapping
 Original environmental mapping technique
 Proposed by Blinn and Newell
 Uses lines of longitude and latitude to map
parametric variables to texture coordinates
 OpenGL supports sphere mapping
 Requires a circular texture map equivalent to an
image taken with a fisheye lens

28. Sphere Map

30. Capturing a Sphere Map

31. For derivation of sphere map, see section 7.8 of your text

32. Light Maps

33. Specular Mapping
 Use a greyscale texture as a multiplier for the
specular component

34. Irradiance Mapping
 You can reuse environment maps for diffuse reflections
 Integrate the map over a hemisphere at each pixel
(basically blurs the whole thing out)

35. Irradiance Mapping Example

36. 3D Textures
 3D volumetric textures exist as well, though you can
only render slices of them in OpenGL
 Generate a full image by stacking up slices in Z
 Used in visualization

37. Procedural Texturing
 Math functions that generate textures

38. Alpha Mapping
 Represent the alpha channel with a texture
 Can give complex outlines, used for plants
Render Bush
on 1 polygon
Render Bush
on polygon rotated
90 degrees

39. Bump mapping
 by Blinn in 1978
 Inexpensive way of simulating wrinkles and bumps
on geometry
 Too expensive to model these geometrically
 Instead let a texture modify the normal at each pixel,
and then use this normal to compute lighting
geometry
Bump map
Stores heights: can derive normals
+ Bump mapped geometry
=

40. Bump mapping: Blinn’s method
 Basic idea:
 Distort the surface along the normal at that point
 Magnitude is equal to value in heighfield at that location

41. Bump mapping: examples

42. Bump Mapping Vs Normal Mapping
 Bump mapping
 (Normals n=(nx , ny , nz) stored as
distortion of face orientation.
Same bump map can be
tiled/repeated and reused for
many faces)
 Normal mapping
 Coordinates of normal (relative to
tangent space) are encoded in
color channels
 Normals stored include face
orientation + plus distortion. )

43. Normal Mapping
 Very useful for making low‐resolution geometry look
like it’s much more detailed

44. Tangent Space Vectors
 Normals stored in local coordinate frame
 Need Tangent, normal and bi‐tangent vectors

45. Displacement Mapping
 Uses a map to displace
the surface geometry
at each position
 Offsets the position
per pixel or per vertex
 Offsetting per vertex is
easy in vertex shader
 Offsetting per pixel is
architecturally hard

46. Parallax Mapping
 Normal maps increase lighting detail, but they lack a
sense of depth when you get up close
 Parallax mapping
 simulates depth/blockage of one part by another
 Uses heightmap to offset texture value / normal lookup
 Different texture returned after offset

47. Relief Mapping
 Implement a heightfield raytracer in a shader
 Pretty expensive, but looks amazing

48. Relief Mapping Example

49. References
 Angel and Shreiner, Interactive Computer Graphics, 6th edition
 Hill and Kelley, Computer Graphics using OpenGL, 3rd edition
 UIUC CS 319, Advanced Computer Graphics Course
 David Luebke, CS 446, U. of Virginia, slides
 Chapter 1‐6 of RT Rendering
 Hanspeter Pfister, CS 175 Introduction to Computer Graphics,
Harvard Extension School, Fall 2010 slides
 Christian Miller, CS 354, Computer Graphics, U. of Texas, Austin
slides, Fall 2011
 Ulf Assarsson, TDA361/DIT220 ‐ Computer graphics 2011,
Chalmers Instititute of Tech, Sweden