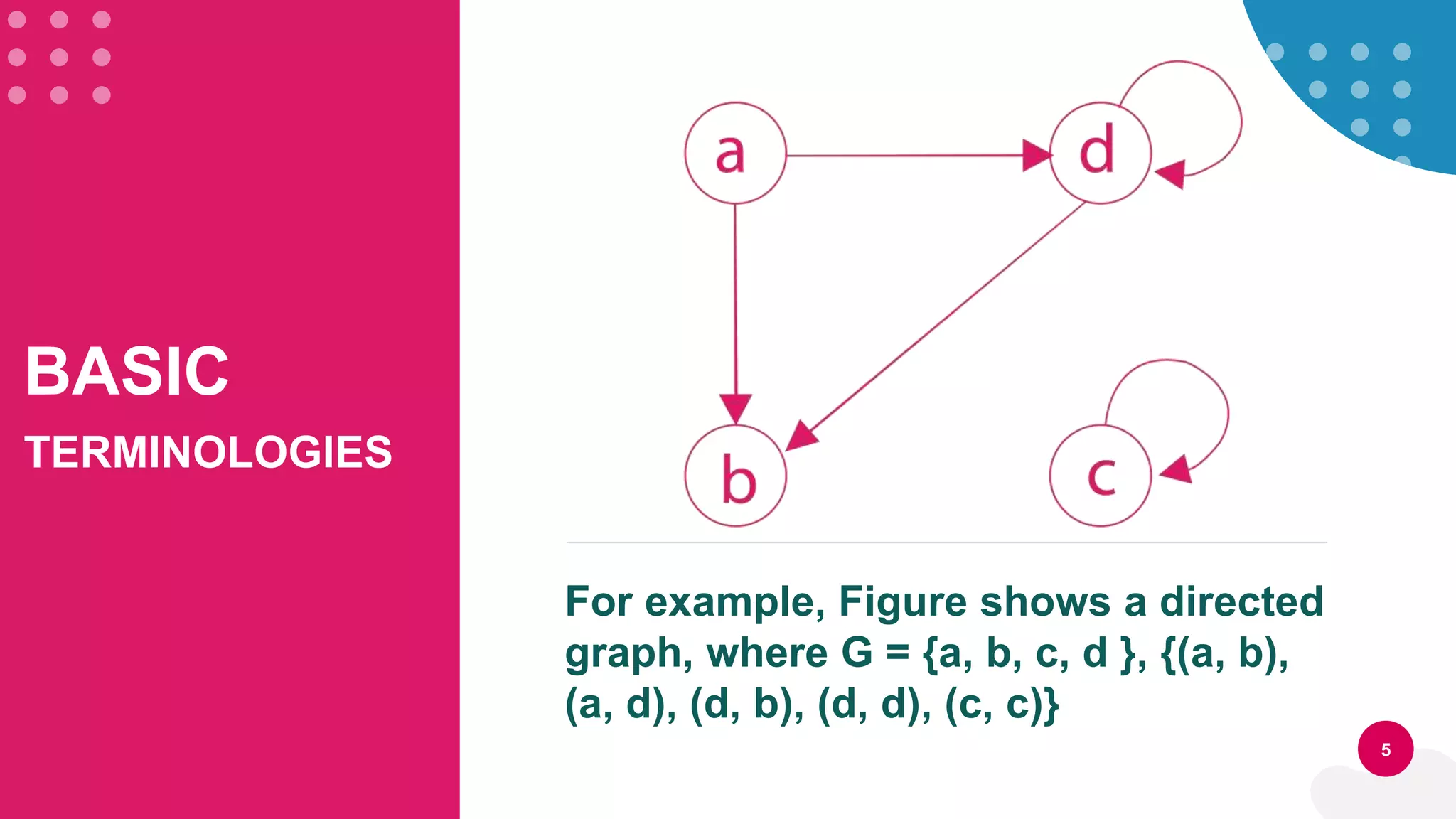
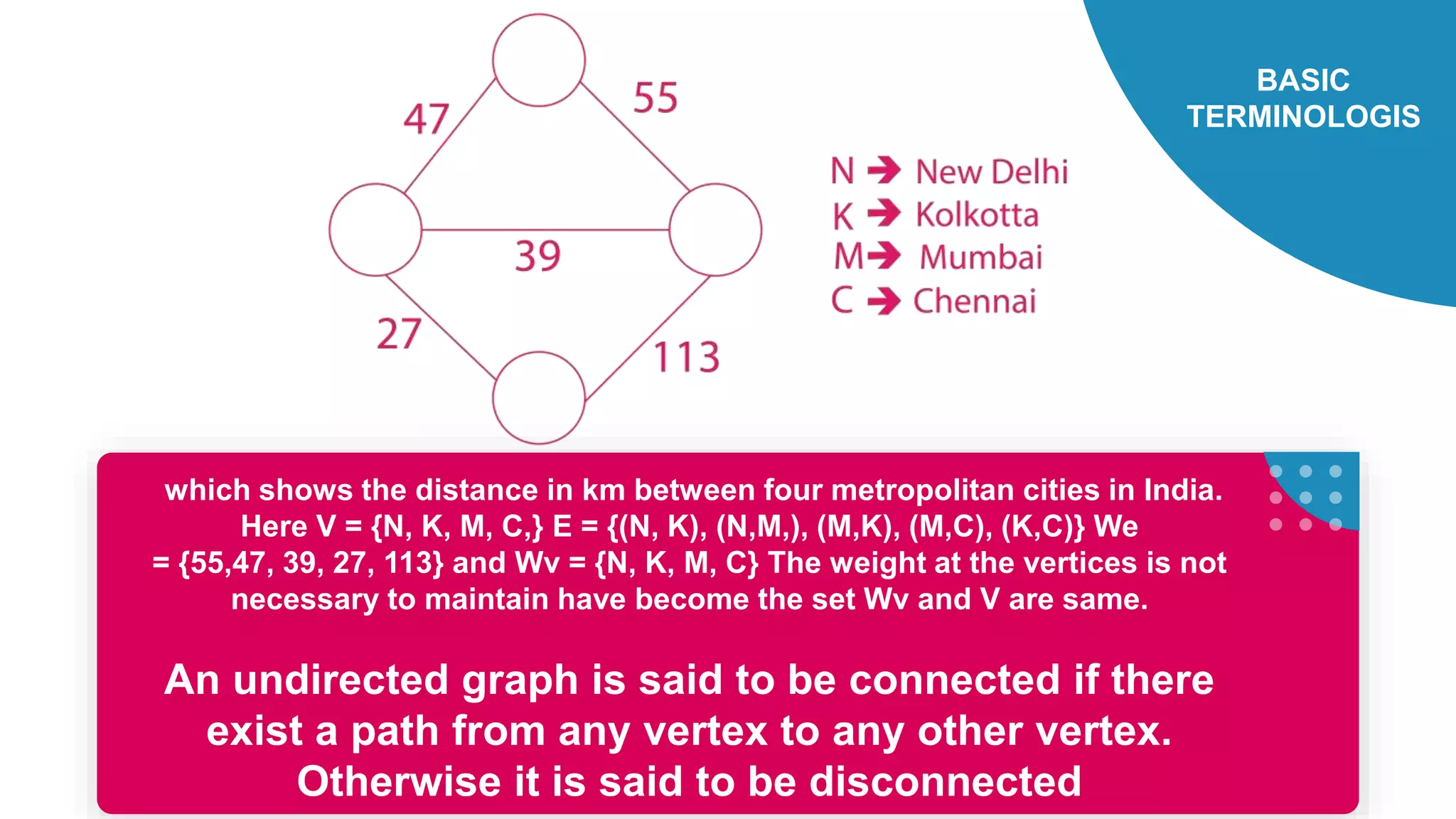
This document discusses three types of graphs: directed graphs, undirected graphs, and weighted graphs. It provides examples and definitions of basic graph terminology like vertices, edges, and paths. It also describes two common ways to represent graphs in computer memory: sequential representation using adjacency lists and linked representation using linked lists. Finally, it outlines high-level processes for creating a graph and searching or deleting elements from a graph.

1. Types Of Graph

2. Tanvir Ahmed Shuvo 182-15-11576
shamiur rahman 172-15-10165
Rifat Mahmud Turag 162-15-8059
Md Abdur Rakib 182-15-11526
Sorwar Hossain 182-15-11672
Group Member List

3. 3
We will
discuss 3
types of
graphs
BASIC
TERMINOLOGIES
REPRESENTATION
OF GRAPH
OPERATIONS
ON GRAPH

4. 4
A directed graph G is defined as an ordered pair (V, E) where,
V is a set of vertices and the ordered pairs in E are called
edges on V. A directed graph can be represented
geometrically as a set of marked points (called vertices) V
with a set of arrows (called edges) E between pairs of points
(or vertex or nodes) so that there is at most one arrow from
one vertex to another vertex.
BASIC TERMINOLOGIES

5. BASIC
TERMINOLOGIES
For example, Figure shows a directed
graph, where G = {a, b, c, d }, {(a, b),
(a, d), (d, b), (d, d), (c, c)}
5

6. which shows the distance in km between four metropolitan cities in India.
Here V = {N, K, M, C,} E = {(N, K), (N,M,), (M,K), (M,C), (K,C)} We
= {55,47, 39, 27, 113} and Wv = {N, K, M, C} The weight at the vertices is not
necessary to maintain have become the set Wv and V are same.
An undirected graph is said to be connected if there
exist a path from any vertex to any other vertex.
Otherwise it is said to be disconnected
BASIC
TERMINOLOGIS

7. shows the disconnected graph,
where the vertex c is not
connected to the graph 7
BASIC
TERMINOLOGIES

8. REPRESENTATION OF GRAPH
The graph is a mathematical structure and finds its
application in many areas, where the problem is to be
solved by computers. The problems related to graph
G must be represented in computer memory using
any suitable data structure to solve the same. There
are two standard ways of maintaining a graph G in
the memory of a computer.

9. TYPES OF REPRESENTATION
OF GRAPH
Sequential representation of a graph using
adjacent
Linked representation of a graph using linked
list

10. 10
LINKED LIST
REPRESENTATION
In this representation (also called
adjacency list representation), we store
a graph as a linked structure. First we
store all the vertices of the graph in a list
and then each adjacent vertices will be
represented using linked list node. Here terminal
vertex of an edge is stored in a structure node and
linked to a corresponding initial vertex in the list

11. 11
The weighted graph can be represented
using a linked list by storing the
corresponding weight along with the terminal
vertex of the edge. Consider a weighted
graph in Figure, it can be represented using a
linked list as in Figure
LINKED LIST
REPRESENTATION

12. OPERATIONS ON GRAPH
12
01
03
02
04
05
CREATING A GRAPH
Input the total number of vertices in the graph, say n
Allocate the memory dynamically for the vertices to store in list array
Input the first vertex and the vertices through which it has edge(s) by
linking the node from list array through nodes.
Repeat the process by incrementing the list array to add other vertices
and edges.
Exit.

13. OPERATIONS ON GRAPH
13
01
03
02
04
05
SEARCHING AND DELETING FROM A
GRAPH
Input an edge to be searched
Search for an initial vertex of edge in list arrays by incrementing the array
index.
Once it is found, search through the link list for the terminal vertex of
the edge.
If found display “the edge is present in the graph”.
Then delete the node where the terminal vertex is found and rearrange
the link list.
06 Exit

14. Thank You
😊