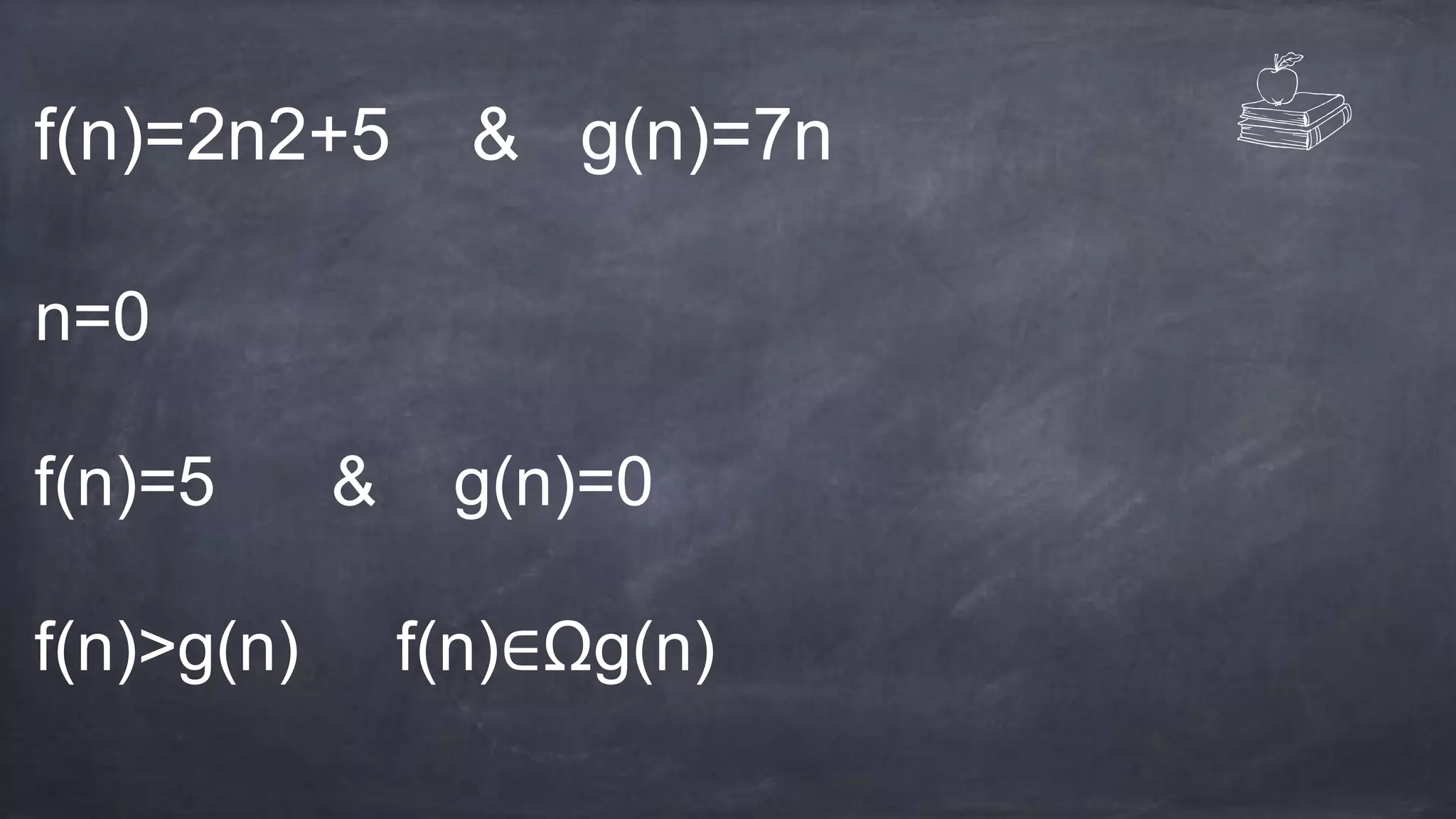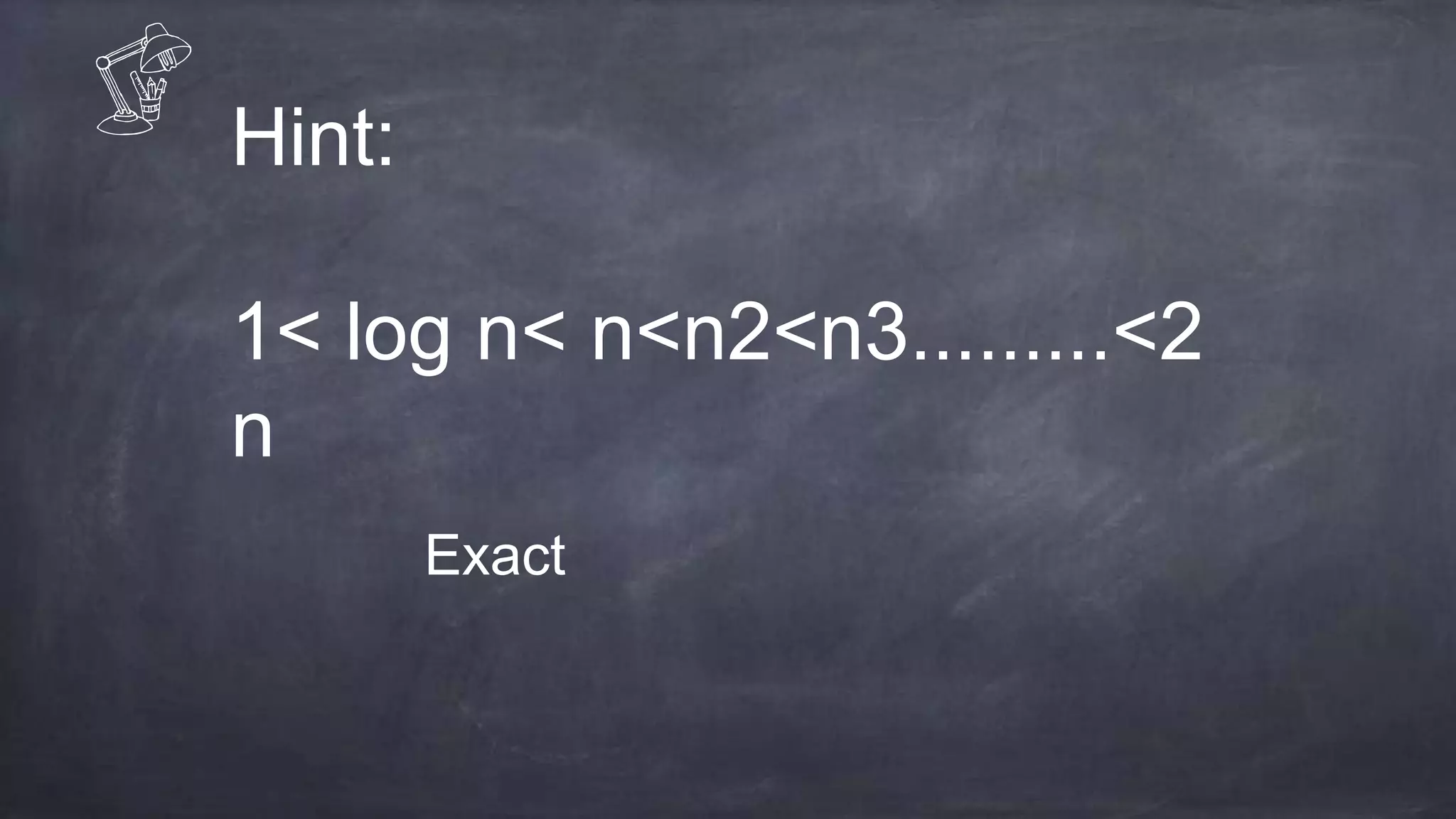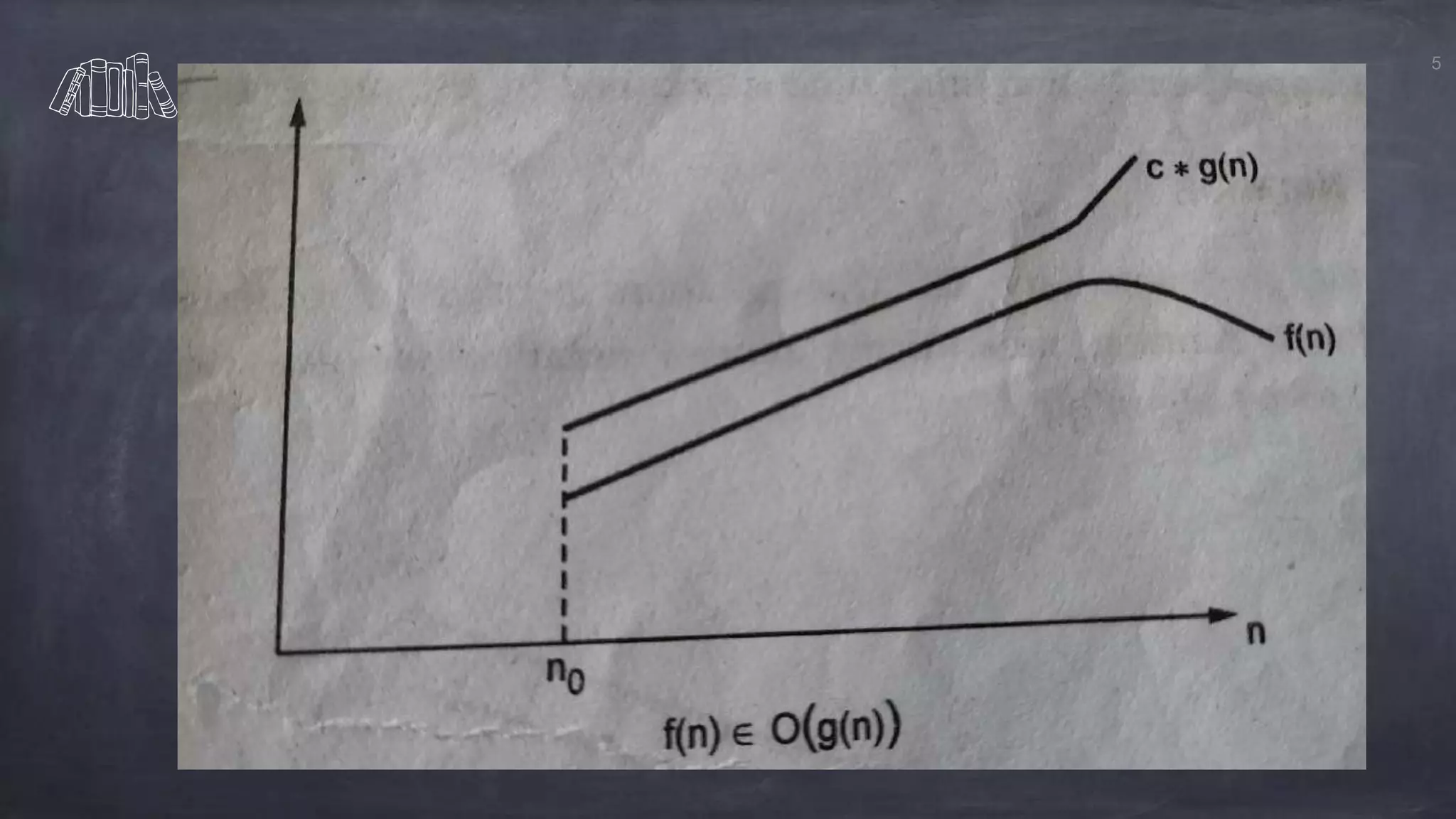
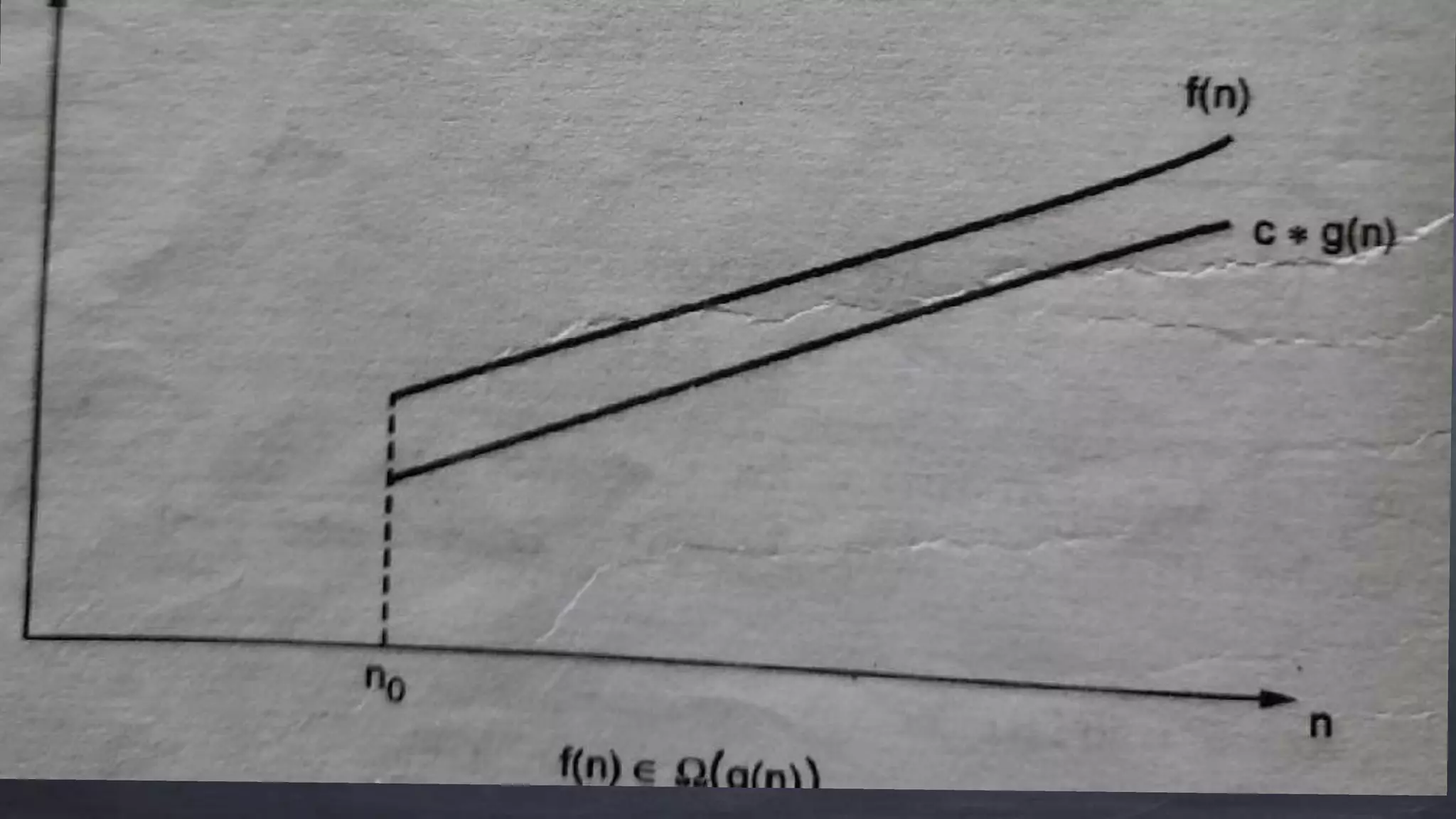
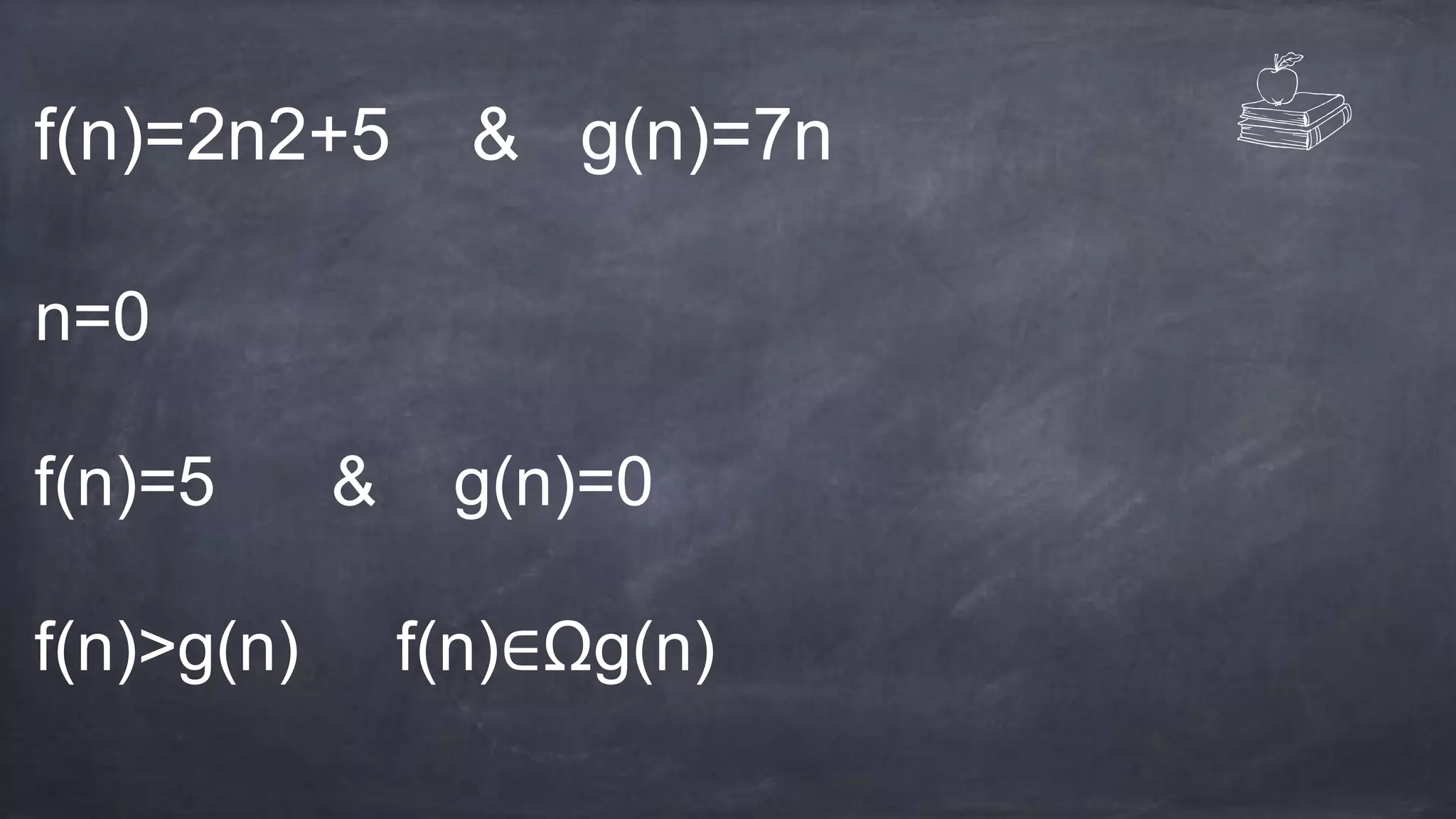
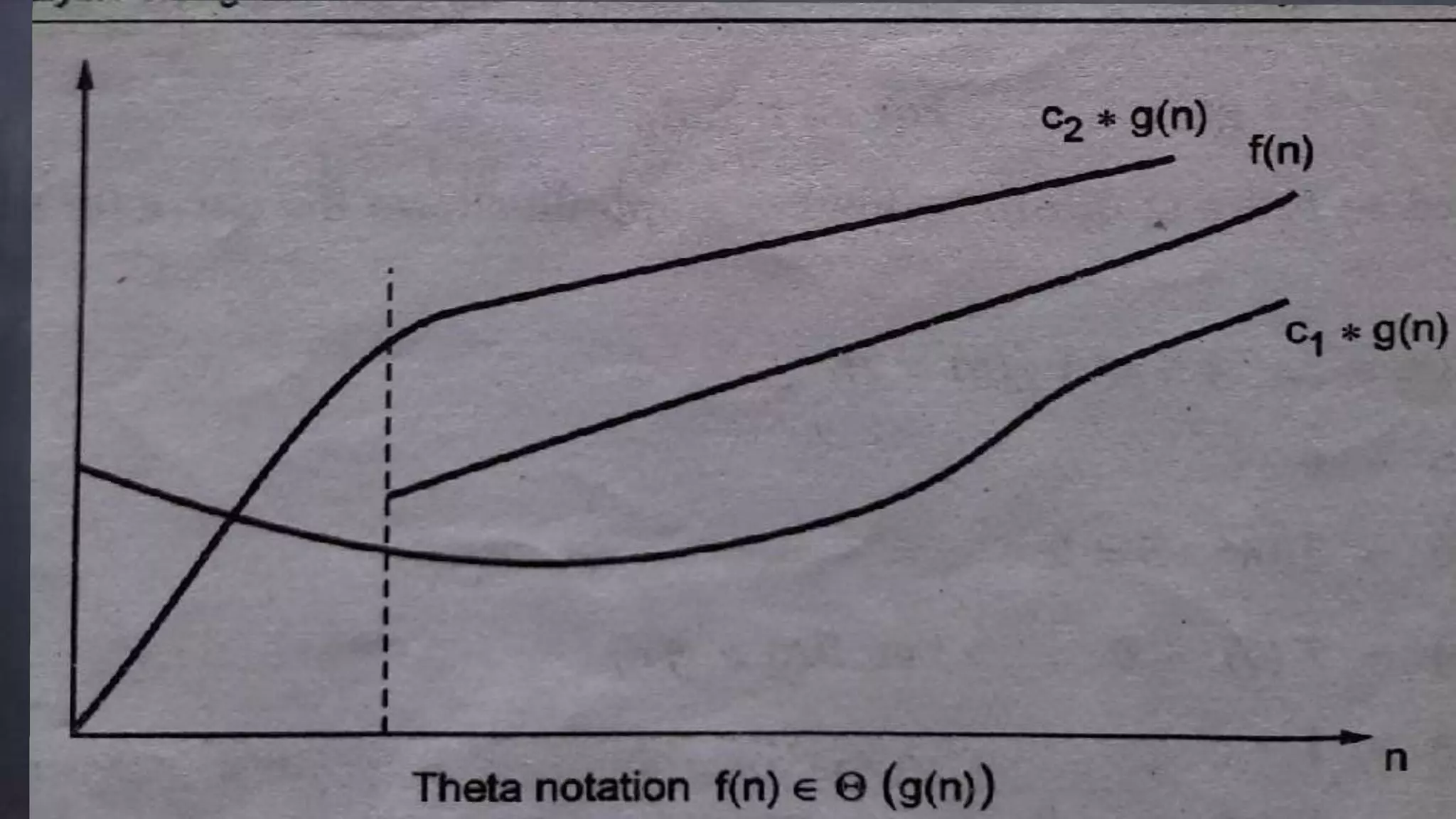
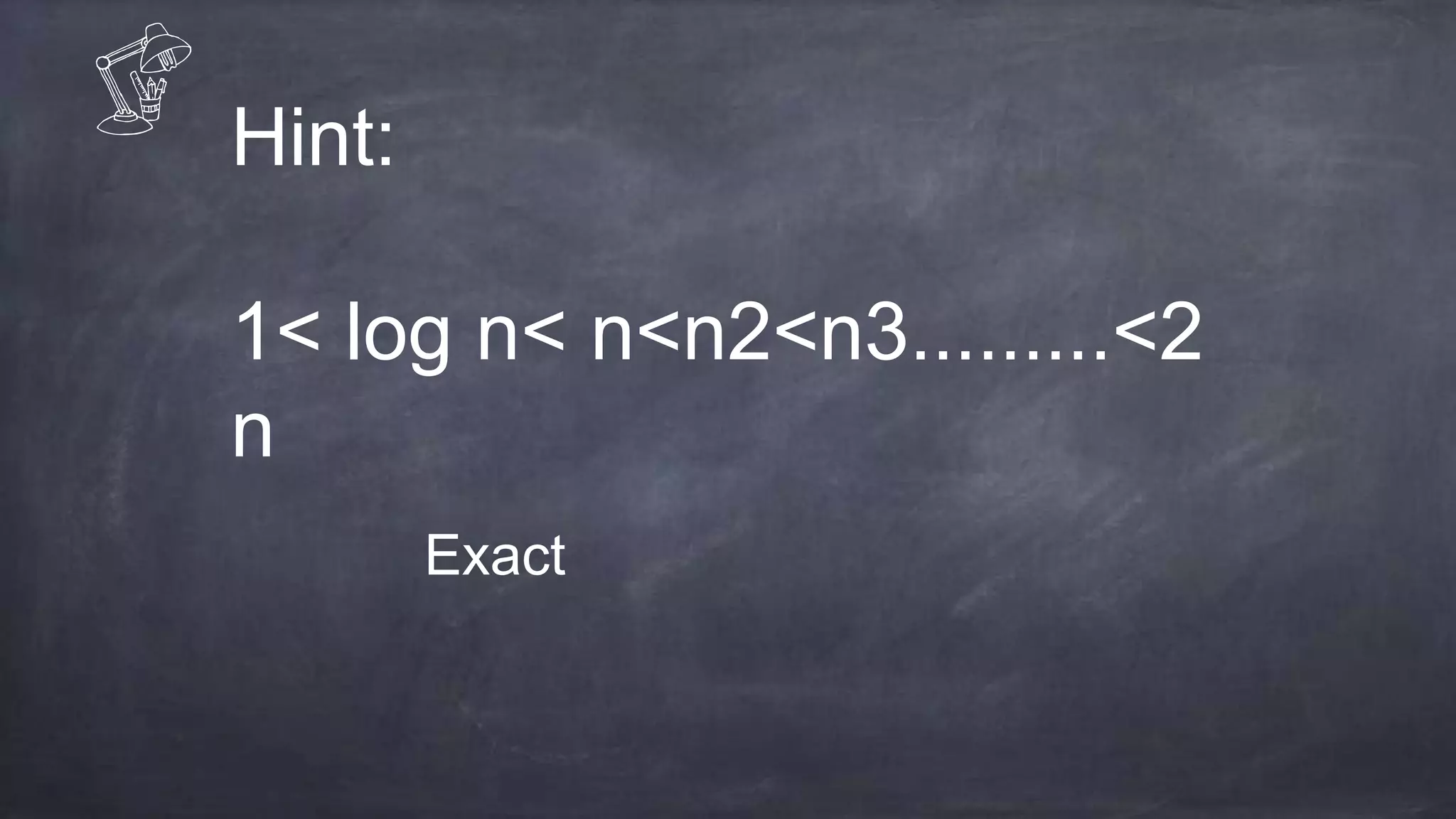
This document discusses asymptotic notations which are mathematical representations used to describe the time complexity of algorithms. It introduces the Big O, Big Omega, and Big Theta notations. Big O notation provides an upper bound on running time. Big Omega provides a lower bound. Big Theta gives a tight bound between the upper and lower bounds such that the running time is equal to both. Examples are provided to demonstrate each notation.

1. Asymptotic Notations

2. The mathametical representation of time c
omplexity is called as Asymtotic Notation
s.
Big oh ( O)notation
Big omegap(Ω)notation
Big theta (θ) notation

3. Big oh (O) notation: It is a method repr
esenting upper bound of algorithm's running
time.
Definition:
Let f(n)& g(n) ---->two non negative function
s.
n0 & c -----> constants
n0 is some input n>n0 , c>0

4. f(n)<=c*g(n)
f(n)∈Og(n)

5. 5
YOUR TITLE
Add your words here according to your need to draw the text box size
YOUR TITLE
Add your words here according to your need to draw the text box size
YOUR TITLE
Add your words here according to your need to draw the text box size
YOUR TITLE
Add your words here according to your need to draw the text box size
Add your title here

6. Example:
f(n)=2n+2 & g(n)=n2
If n=3
f(n)=2(3)+2=8
g(n)=(3)2=9
f(n)<g(n)

7. 90%
Big omega(Ω)notation
This represents lower boun
d of algorithm running time.
f(n)>=c*g(n)

9. f(n)=2n2+5 & g(n)=7n
n=0
f(n)=5 & g(n)=0
f(n)>g(n) f(n)∈Ωg(n)

10. Theta notation :(θ )
By this method tbe running time is betw
een upper bound and lower bound.
C1*g(n)<=f(n)<=c2*g(n)
Then say that
f(n)∈θg(n)

12. Example:
If f(n)=2n+8 & g(n)=7n
I e 5n<2n+8<7n n>=2

13. Hint:
1<log n<n<n2<n3........<2n
Upper bond

14. Hint:
1< log n < n< n2<n3........< 2n
Lower bound

15. Hint:
1< log n< n<n2<n3.........<2
n
Exact