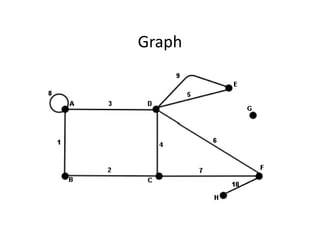
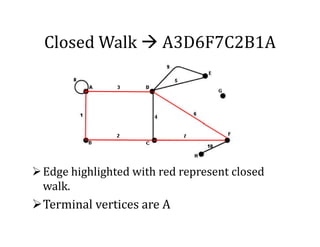
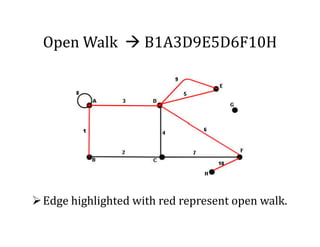
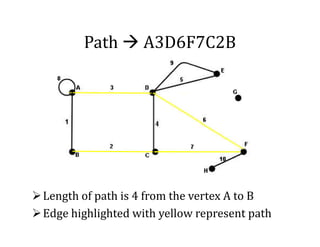
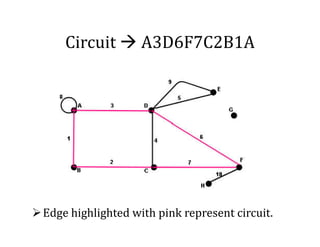
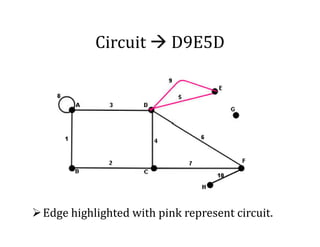
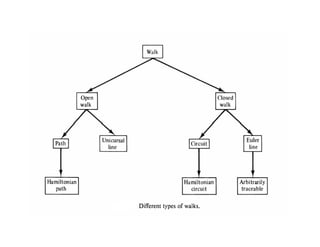
This document provides an introduction to graph theory, detailing the definitions and properties of graphs, including vertices, edges, and concepts like walks, paths, and circuits. It explains various terms such as self-loops, parallel edges, isolated vertices, and the degrees of vertices, along with examples of each. Additionally, the document addresses open and closed walks, as well as the distinctions between paths and circuits.

1. GRAPH THEORY
Introduction
Walk
PathPath
Circuit
Dr Manish T I
Associate Professor,
Dept of CSE
ASIET, Kalady

2. Definition
• A graph G = ( V , E ) consists of a set of
objects V = { v1 , v2 , v3 ,….., vn} called vertices
and another set E = = { e1 , e2 , e3 ,….., em}
whose elements are called edges, such thatwhose elements are called edges, such that
each edge ek is identified with an unordered
pair ( vi, vj) of vertices.
• Here discussion is based on undirected graph.

3. Graph

4. Properties of Graph
When a vertex vi is an end vertex of some edge ej
vi and ej are said to be Incident with each other.
In above Graph G for example
Edge 1,2 are Incident on Vertex B
Edge 1,3,8 are Incident on Vertex A

5. • An edge having the same vertex as both its end
vertices is called a self-loop.
• More than one edge associated with a given pair of
vertices. Such edges are referred as parallel edges
In above Graph G for exampleIn above Graph G for example
 Edge 8 has vertex A has its end vertices. Hence
Edge 8 is a self-loop
 Edge 5, 9 are associated with vertex D,E. Hence
Edge 5, 9 are parallel edges.

6. A vertex having no incident edge is called an
isolated vertex.
The number of edges incident on a vertex vi ,
with self-loops counted twice is called the
degree d(vi), of vertex vi . Degree is also known
as the Valency.as the Valency.
A vertex of degree one is called a pendant
vertex or an end vertex.
A Graph has edge set empty then it called null
graph

7. Degree of Vertices in a Graph given
d(A) = 1+2+1 = 4 * Value 2 represents self-loop
d(B)= 1+1 = 2
d(C)= 1+1+1 = 3
d(D)=1+1+1+1+1 =5
d(E)= 1+1=2
d(F)=1+1+1=2
d(G)=0  Isolated vertex.
d(H)=1  Pendant vertex

8. Null Graph
Degree of all vertices in the null graph is zero.
All vertices in the null graph is isolated vertex.

9. WALKS
• A Walk is defined as a finite alternating sequence
of vertices and edges beginning and ending with
vertices, such that each edge is incident with the
vertices preceding and following it.
 No edge appears more than once in a walk
 A vertex may appear more than once.

10. • Walk is also known as Edge train or a Chain.
• The set of vertices and edges constituting a given
walk in a graph G is clearly a sub graph of G.
• A vertices with which a walk begins and ends are
known as Terminal vertices.known as Terminal vertices.
• A walk to begin and end at the same vertex is
known as Closed walk. Otherwise walk is known
as Open walk.

11. Closed Walk  A3D6F7C2B1A
Edge highlighted with red represent closed
walk.
Terminal vertices are A

12. Open Walk  B1A3D9E5D6F10H
Edge highlighted with red represent open walk.

13. • An open walk in which no vertex appears more than
once is called a Path. (Simple path or Elementary path)
• The number of edges in a path is called Length of
Path.
PATH & CIRCUIT
Path.
• Self-loop can be included in a Walk but not in a Path.
• A closed walk in which no vertex appears more than
once except terminal vertices is called a Circuit.

14. Path  A3D6F7C2B
Length of path is 4 from the vertex A to B
Edge highlighted with yellow represent path

15. Circuit  A3D6F7C2B1A
Edge highlighted with pink represent circuit.

16. Circuit  D9E5D
Edge highlighted with pink represent circuit.

18. References
• Narasingh Deo, “Graph theory with
applications to engineering and
computer science”, PHI.
• Graph drawings www.draw.io• Graph drawings www.draw.io
Any comments, corrections and feedback send to
manishti2004@gmail.com
manish.cs@adishankara.ac.in