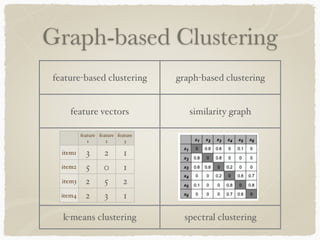
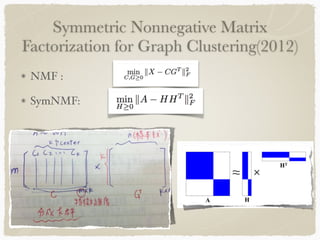
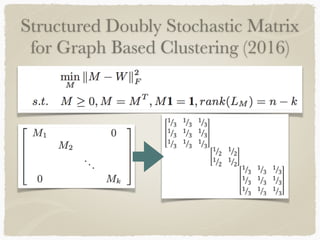
Graph-based clustering uses similarity graphs instead of feature vectors, representing data as a graph where nodes are data points and edges represent similarity. It can handle any data type as long as similarities are defined, and is useful for high-dimensional data by reducing dimensionality. However, computing similarities between all pairs of data points is computationally expensive. Survey papers discussed algorithms like spectral clustering and modularity optimization. Applications include document analysis, social networks, and recommendation systems. Future work includes determining optimal cluster numbers, scaling to large data, and handling directed graphs.

1. Graph-Based Clustering
Yi-Hsiu Lin
2016-8-29

2. Key Points
Graph-based Clustering
Survey Papers
Applications ＆ Future works

3. Graph-based Clustering
feature-based clustering graph-based clustering
feature vectors similarity graph
k-means clustering spectral clustering
feature
1
feature
2
feature
3
item1 3 2 1
item2 5 0 1
item3 2 5 2
item4 2 3 1

4. Advantages
It can be used with virtually any data type as long
as appropriate similarity functions are defined
Similarity function itself make sure that points
which are considered to be “very similar” by the
function are also closely related in the application the
data comes from
High dimensional scenario - noise effects of locally
irrelevant attributes - reduce the high-dimensionality
of the feature space via a similarity metric

5. Disadvantages
Time complexity for creating the similarity matrix
scales with the square of the number of data points
Evaluating the similarity of two vertices may
turn out to be a task even more complex than
the clustering of the graph once the similarities are
known

6. Similarity measure
similarity measure (2007)
cosine similarity
Gaussian similarity
Jaccard similarity

7. Similarity measure
Document analysis - frequency inverse-documents-frequency
( tf-idf )
Term Frequency (tf), Inverse Document Frequency (idf)
distance measure cosine similarity
fish sea human
Doc 1 5 2 1
Doc 2 2 1 0
Doc 3 2 8 7
Doc 4 7 7 0

8. Survey Papers
Spectral clustering (1973)
Modularity (2006)
SymNMF (2012)
Fuzzy Modularity (2013)
SoF (2015)
Structured Stochastic Doubly Matrix (2016)

9. A Tutorial on Spectral
Clustering (1973)
Pre-processing
construct a similarity matrix
Decomposition
compute eigenvalues and eigenvectors of the matrix
map each point to a lower - dimensional representation
based on one or more eigenvectors
Grouping
Assign points to two or more clusters

10. A Tutorial on Spectral
Clustering (1973)
construct similarity graph
compute L ( L=D-W)
compute first k eigenvectors of L
let U= ,
be the vectors corresponding to i-th row
of U
cluster the points with the k-means algorithm

11. Modularity and community structure in
networks(2006)
A Soft Modularity Function For Detecting Fuzzy
Communities in Social Networks (2013)
Modularity : (Evaluate the clustering results)
(the number of edges falling within groups) - (the
expected number in an equivalent network with edges
placed at random)
Modularity Matrix :
Fuzzy Modularity :

12. Symmetric Nonnegative Matrix
Factorization for Graph Clustering(2012)
NMF :
SymNMF:

13. SoF: Soft-Cluster Matrix Factorization
for Probabilistic Clustering (2015)
Co-cluster Probability

14. Structured Doubly Stochastic Matrix
for Graph Based Clustering (2016)

15. Time Complexity

16. Space Complexity

17. Future works

18. Soft/Fuzzy Clustering
The data objects has membership weight that is between
0 to 1, thus data points can potentially belong to multiple
clusters — Natural Grouping
Applications
Documents with multiple theme
Marketing
Recommendation system

19. Applications & Future works
Algorithms
the affinity measure
the normalization of the affinity matrix
the particular clustering algorithm
How to determine the number of cluster ?
How to deal with high quantity of data ?
How to deal with directed graph ?

20. Applications & Future works
Social networks
epidemic network
transportation
position

21. Applications & Future works

23. Reference
Similarity-Based Clustering: Recent Developments and Biomedical Applications - Thomas Villmann，M.
Biehl，Barbara Hammer
Graph clustering - Satu Elisa Schaeffer∗ Laboratory for Theoretical Computer Science, Helsinki University
of Technology TKK, P.O. Box 5400, FI-02015 TKK, Finland
Symmetric Nonnegative Matrix Factorization for Graph Clustering - Da Kuang∗ Chris Ding† Haesun Park
SoF: Soft-Cluster Matrix Factorization for Probabilistic Clustering - Han Zhao† , Pascal Poupart† , Yongfeng
Zhang§ and Martin Lysy‡
A Soft Modularity Function For Detecting Fuzzy Communities in Social Networks - Timothy C. Havens
Modularity and community structure in networks - M. E. J. Newman*
ATutorial on Spectral Clustering - Ulrike von Luxburg
Survey Graph clustering - Satu Elisa Schaeffer
Structured Doubly Stochastic Matrix for Graph Based Clustering