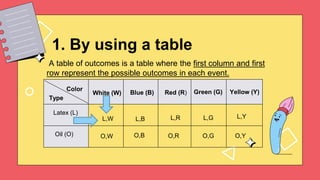
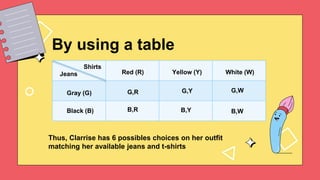
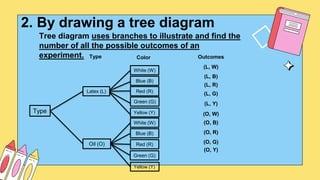
This document provides examples and explanations of different methods for counting outcomes of experiments: 1. Tables can be used to systematically list all combinations of outcomes in experiments with multiple variables. 2. Tree diagrams visually illustrate the branching possibilities in an experiment. 3. Systematic listing ensures all outcomes are included without omissions or duplicates. 4. The fundamental counting principle of multiplying the number of possible outcomes in each variable provides the total without explicit listing.

1. WELCOME
GRADE 8
8th grade
Jezelyn C. Fabelinia

2. Counting the Number of
Occurrence of an
Outcome in an
Experiment
8th grade

3. Counting an Outcome in an
Experiment
a. Table
b. Tree diagram
c. Systematic listing
d. Fundamental Counting
Principles

4. Example 1:
A paint manufacturer is planning to
produce different paints. The
categories include
Type: latex (L), oil (O)
Color: white (W), blue (B), red (R), green (G), yellow
(Y)
How many kinds of paint can be made
if he plans to select one type and one
color?

5. 1. By using a table
Color
Type
A table of outcomes is a table where the first column and first
row represent the possible outcomes in each event.
Latex (L)
Oil (O)
White (W) Blue (B) Red (R) Green (G) Yellow (Y)
L,W
O,W
L,B L,R L,G L,Y
O,B O,R O,G O,Y

6. 2. By drawing a tree diagram
Tree diagram uses branches to illustrate and find the
number of all the possible outcomes of an
experiment.
Type
Latex (L)
Oil (O)
White (W)
Blue (B)
Red (R)
Green (G)
Yellow (Y)
White (W)
Blue (B)
Red (R)
Green (G)
Yellow (Y)
Type Color Outcomes
(L, W)
(L, B)
(L, R)
(L, G)
(L, Y)
(O, B)
(O, W)
(O, R)
(O, G)
(O, Y)

7. It is the process of listing all the possible outcomes of
an event in an organized or systematic manner to
ensure that the outcomes are complete.
3. By systematic listing
(L,W)
(L,B)
(L,R)
(L,G)
(L,Y)
(O,W)
(O,B)
(O,R)
(O,G)
(O,Y)

8. The fundamental counting principle is a technique of
finding the number of possible outcomes of an
experiment without listing.
4. By applying the Fundamental Counting
Principles
(No. of Types) x (No. of Colors) = (No. of possible
outcomes)
2 x 5 = 10 possible outcomes

9. Example 1:
Clarisse wanted to go the Shopping Mall. She was confused
on what to wear. In her wardrobe she found a gray (G) and a
black (B) jeans and a red (R), a yellow (Y) and a white (W)
shirts. Help Clarisse choose her outfit matching her available
jeans and t-shirts using the following methods.
a. Table
b. Tree Diagram
c. FCP

10. By using a table
Jeans
Shirts
Gray (G)
Black (B)
Red (R) Yellow (Y) White (W)
G,R G,Y G,W
B,R B,Y B,W
Thus, Clarrise has 6 possibles choices on her outfit
matching her available jeans and t-shirts

11. By using a Tree diagram
Jeans Shirts Outcomes
Gray (G)
Black (B)
Red (R)
Yellow (Y)
White (W)
Red (R)
Yellow (Y)
White (w)
G,R
G,Y
G,W
B,R
B,Y
B,W

12. A
Suppose a shopping mall has four doors. In how many ways can a
customer enter and leaving the shopping mall? How many possible ways
of entering and leaving the mall by using Fundamental Counting Principles.
.
B C D
Example 2:

13. By systematic listing
Entrance Doors = {A, B, C, D}
Exit Doors = {A, B, C, D}
Thus, the costumer can enter and leave in 16 possible ways
AA, AB, AC, AD
BA, BB, BC, BD
CA, CB, CC, CD
DA, DB, DC, DD

14. Fundamental Counting Principles
Entrance
Door
Exit
Door
Numer of
Possible
Outcomes
X =
4
X
4 = 16
16 possible oucotmes

15. Situations
A person wants to buy one fountain pen, one ball pen and one
pencil from a stationery shop. If there are 10 fountain pen varieties,
12 ball pen varieties and 5 pencil varieties, in how many ways can he
select these articles ?
Given 7 flags of different colors, how many different signals can
be generated if a signal requires the use of two flags, one below
the other ? Formula : m x n = number of possible outcome
Formula : m x n x p = number of possible outcome
7 x 6 = number of possible outcome
42 ways
10 x 12 x 5 = number of possible outcome
600 ways

16. Situations
Fourteen students compete in a race. In how
many ways first three prizes be given ?
Formula : m x n x p = number of possible outcome
14 x 13 x 12= number of possible outcome
2,184 ways

17. Situations
From among the 36 teachers in a college, one
principal, one vice-principal and the teacher-in charge
are to be appointed. In how many ways this can be
done ?
Formula : m x n x p = number of possible outcome
36 x 35 x 34= number of possible outcome
42,840 ways

18. 1. Naomi has 5 pairs of socks (A, B, C, D, E) and 2
pairs of shoes (1, 2) which he uses when he goes to
church. How many ways can he use his pairs of socks
and shoes? Find the possible outcomes using these
following methods.
a. Table
b. Systematic listing
c. Tree diagram
d. Applying the fundamental Counting principles
Activity 1. What’s My Outfit?

19. Assingment . It’s lunch time
A school canteen offers a student meal. It is composed of cup of rice, a
vegetable viand, a meat viand, and a regular drink. If there are 3
vegetable viands (pinakbet, chop suey, or mixed vegetables), 3 meat
viands (afritada, adobong baboy, or beef steak), and 2 drinks (lemon
juice, or kalamansi juice) .Find the possible outcomes using these
following methods.
A. Systematic listing
B. Tree diagram
C. Applying the fundamental Counting principles

20. Thank you!