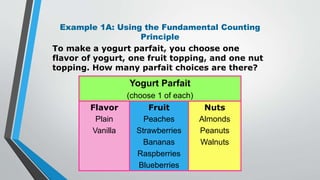
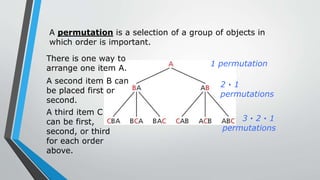
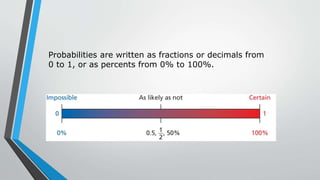
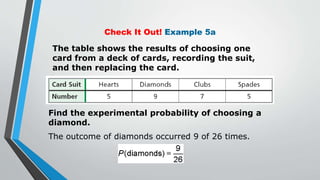
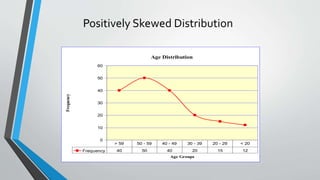
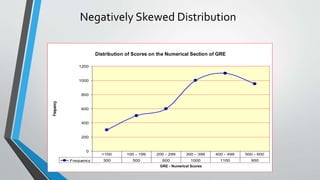
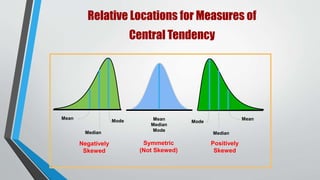
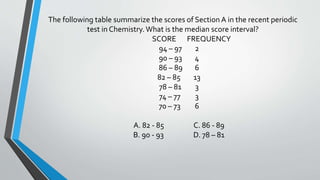
This document discusses statistics and probability concepts such as the fundamental counting principle, permutations, combinations, theoretical probability, and experimental probability. It provides examples of how to use these concepts to calculate the number of possible outcomes in probability experiments and real-world scenarios. For instance, it shows how to use permutations and combinations to determine the number of ways a student government can select officers from a group of people or how many combinations there are to draw a set of cubes from a bag. It also demonstrates calculating theoretical probabilities, such as the likelihood of rolling certain numbers on dice, and experimental probabilities based on data from trials.

1. Statistics and Probability
BY: DR. ARCHIEVAL A. RODRIGUEZ

2. Evaluate.
1. 5  4  3  2  1
2. 7  6  5  4  3  2  1
3. 4.
5. 6.
120
5040
4 210
10 70

3. Solve problems involving the
Fundamental Counting Principle.
Solve problems involving permutations
and combinations.
Objectives

4. You have previously used
tree diagrams to find
the number of possible
combinations of a group of
objects. In this lesson, you
will learn to use the
Fundamental Counting
Principle.

6. Example 1A: Using the Fundamental Counting
Principle
To make a yogurt parfait, you choose one
flavor of yogurt, one fruit topping, and one nut
topping. How many parfait choices are there?
Yogurt Parfait
(choose 1 of each)
Flavor
Plain
Vanilla
Fruit
Peaches
Strawberries
Bananas
Raspberries
Blueberries
Nuts
Almonds
Peanuts
Walnuts

7. Example 1A Continued
number
of
flavors
times
number
of fruits
number
of nuts
times equals
number
of choices
2  5  3 = 30
There are 30 parfait choices.

8. Example 1B: Using the Fundamental Counting
Principle
A password for a site consists of 4 digits
followed by 2 letters. The letters A and Z are
not used, and each digit or letter may be used
more than once. How many unique passwords
are possible?
digit digit digit digit letter letter
10  10  10  10  24  24 = 5,760,000
There are 5,760,000 possible passwords.

9. Check It Out! Example 1a
A “make-your-own-adventure” story lets you
choose 6 starting points, gives 4 plot choices,
and then has 5 possible endings. How many
adventures are there?
number
of
starting
points

number
of plot
choices
number
of
possible
endings
 =
number
of
adventures
6  4  5 = 120
There are 120 adventures.

10. Check It Out! Example 1b
A password is 4 letters followed by 1 digit.
Uppercase letters (A) and lowercase letters (a)
may be used and are considered different. How
many passwords are possible?
Since both upper and lower case letters can be used,
there are 52 possible letter choices.
letter letter letter letter number
52  52  52  52  10 = 73,116,160
There are 73,116,160 possible passwords.

11. A permutation is a selection of a group of objects in
which order is important.
There is one way to
arrange one item A.
A second item B can
be placed first or
second.
A third item C
can be first,
second, or third
for each order
above.
1 permutation
2 · 1
permutations
3 · 2 · 1
permutations

12. You can see that the number of permutations of 3 items
is 3 · 2 · 1. You can extend this to permutations of n
items, which is n · (n – 1) · (n – 2) · (n – 3) · ... · 1.
This expression is called n factorial, and is written as n!.

14. Sometimes you may not want to order an entire set of
items. Suppose that you want to select and order 3
people from a group of 7. One way to find possible
permutations is to use the Fundamental Counting
Principle.
First
Person
Second
Person
Third
Person
There are 7 people.
You are choosing 3
of them in order.
7
choices
6
choices
5
choices
  =
210
permutations

15. arrangements of 4 4! 4 · 3 · 2 · 1
Another way to find the possible permutations is to use
factorials. You can divide the total number of
arrangements by the number of arrangements that are
not used. In the previous slide, there are 7 total people
and 4 whose arrangements do not matter.
arrangements of 7 = 7! = 7 · 6 · 5 · 4 · 3 · 2 · 1 = 210
This can be generalized as a formula, which is useful
for large numbers of items.

17. Example 2A: Finding Permutations
How many ways can a student government
select a president, vice president, secretary, and
treasurer from a group of 6 people?
This is the equivalent of selecting and arranging 4
items from 6.
= 6 • 5 • 4 • 3 = 360
Divide out common factors.
There are 360 ways to select the 4 people.
Substitute 6 for n and 4 for r in

18. Example 2B: Finding Permutations
How many ways can a stylist arrange 5 of 8
vases from left to right in a store display?
Divide out common
factors.
= 8 • 7 • 6 • 5 • 4
= 6720
There are 6720 ways that the vases can be arranged.

19. Check It Out! Example 2a
Awards are given out at a costume party. How
many ways can “most creative,” “silliest,” and
“best” costume be awarded to 8 contestants if
no one gets more than one award?
= 8 • 7 • 6
= 336
There are 336 ways to arrange the awards.

20. Check It Out! Example 2b
How many ways can a 2-digit number be formed
by using only the digits 5–9 and by each digit
being used only once?
= 5 • 4
= 20
There are 20 ways for the numbers to be formed.

21. A combination is a grouping of items in which order
does not matter. There are generally fewer ways to
select items when order does not matter. For
example, there are 6 ways to order 3 items, but they
are all the same combination:
6 permutations  {ABC, ACB, BAC, BCA, CAB, CBA}
1 combination  {ABC}

22. To find the number of combinations, the formula for
permutations can be modified.
Because order does not matter, divide the number of
permutations by the number of ways to arrange the
selected items.

24. When deciding whether to use permutations or
combinations, first decide whether order is important.
Use a permutation if order matters and a combination
if order does not matter.

25. You can find permutations and combinations by
using nPr and nCr, respectively, on scientific and
graphing calculators.
Helpful Hint

26. Example 3: Application
There are 12 different-colored cubes in a bag.
How many ways can Randall draw a set of 4
cubes from the bag?
Step 1 Determine whether the problem represents
a permutation of combination.
The order does not matter. The cubes may be
drawn in any order. It is a combination.

27. Example 3 Continued
= 495
Divide out
common
factors.
There are 495 ways to draw 4 cubes from 12.
5
Step 2 Use the formula for combinations.
n = 12 and r = 4

28. Check It Out! Example 3
The swim team has 8 swimmers. Two swimmers
will be selected to swim in the first heat. How
many ways can the swimmers be selected?
= 28
The swimmers can be selected in 28 ways.
4
Divide out
common
factors.
n = 8 and r = 2

29. Probability is the measure of how likely an event is
to occur. Each possible result of a probability
experiment or situation is an outcome. The sample
space is the set of all possible outcomes. An event is
an outcome or set of outcomes.

30. Probabilities are written as fractions or decimals from
0 to 1, or as percents from 0% to 100%.

31. Equally likely outcomes have the same chance of
occurring. When you toss a fair coin, heads and tails
are equally likely outcomes. Favorable outcomes are
outcomes in a specified event. For equally likely
outcomes, the theoretical probability of an event is
the ratio of the number of favorable outcomes to the
total number of outcomes.

32. Example 1A: Finding Theoretical Probability
Each letter of the word PROBABLE is written on
a separate card. The cards are placed face down
and mixed up. What is the probability that a
randomly selected card has a consonant?
There are 8 possible outcomes and 5 favorable
outcomes.

33. Example 1B: Finding Theoretical Probability
Two number cubes are
rolled. What is the
probability that the
difference between the two
numbers is 4?
4 outcomes with a
difference of 4: (1, 5),
(2, 6), (5, 1), and (6, 2)
There are 36 possible outcomes.

34. Check It Out! Example 1a
A red number cube and a
blue number cube are
rolled. If all numbers are
equally likely, what is the
probability of the event?
The sum is 6.
5 outcomes with a sum of 6:
(1, 5), (2, 4), (3, 3), (4, 2)
and (5, 1)
There are 36 possible outcomes.

35. Check It Out! Example 1b
A red number cube and a
blue number cube are
rolled. If all numbers are
equally likely, what is the
probability of the event?
The difference is 6.
0 outcomes with a
difference of 6
There are 36 possible outcomes.

36. Check It Out! Example 1c
A red number cube and a
blue number cube are
rolled. If all numbers are
equally likely, what is the
probability of the event?
The red cube is greater.
15 outcomes with a red greater
than blue: (2, 1), (3, 1), (4, 1),
(5, 1), (6, 1), (3, 2), (4, 2), (5,
2), (6, 2), (4, 3), (5, 3), (6, 3),
(5, 4), (6, 4) and (6, 5).
There are 36 possible outcomes.

37. The sum of all probabilities in the sample space is 1.
The complement of an event E is the set of all
outcomes in the sample space that are not in E.

38. Example 2: Application
There are 25 students in study hall. The table
shows the number of students who are
studying a foreign language. What is the
probability that a randomly selected student is
not studying a foreign language?
Language Number
French 6
Spanish 12
Japanese 3

39. Example 2 Continued
Use the complement.
There are 21
students studying a
foreign language.
There is a 16% chance that the selected student is
not studying a foreign language.
P(not foreign) = 1 – P(foreign)
, or 16%

40. Check It Out! Example 2
Two integers from 1 to 10 are randomly
selected. The same number may be chosen
twice. What is the probability that both
numbers are less than 9?
Use the complement.
P(number < 9) = 1 – P(number  9)
The probability that both numbers are less than 9, is

41. You can estimate the probability of an event by using
data, or by experiment. For example, if a doctor
states that an operation “has an 80% probability of
success,” 80% is an estimate of probability based on
similar case histories.
Each repetition of an experiment is a trial. The sample
space of an experiment is the set of all possible
outcomes. The experimental probability of an event
is the ratio of the number of times that the event
occurs, the frequency, to the number of trials.

42. Experimental probability is often used to estimate
theoretical probability and to make predictions.

43. Example 5A: Finding Experimental Probability
The table shows the results of a spinner
experiment. Find the experimental probability.
Number Occurrences
1 6
2 11
3 19
4 14
spinning a 4
The outcome of 4
occurred 14 times out
of 50 trials.

44. Example 5B: Finding Experimental Probability
The table shows the results of a spinner
experiment. Find the experimental probability.
Number Occurrences
1 6
2 11
3 19
4 14
spinning a number
greater than 2
The numbers 3 and 4 are
greater than 2.
3 occurred 19 times
and 4 occurred 14
times.

45. Check It Out! Example 5a
The table shows the results of choosing one
card from a deck of cards, recording the suit,
and then replacing the card.
Find the experimental probability of choosing a
diamond.
The outcome of diamonds occurred 9 of 26 times.

46. Check It Out! Example 5b
The table shows the results of choosing one
card from a deck of cards, recording the suit,
and then replacing the card.
Find the experimental probability of choosing a
card that is not a club.
Use the complement.

47. Here are raw scores in a quiz: 97, 95, 85, 83, 77, 75, 50,
10, 5, 2, 1. To get a picture of the group’s performance,
which measure of central tendency is most reliable?
A. Mode C. Median
B. Mean D. None. It is best to look at the individual scores

48. Here are raw scores in a quiz: 97, 95, 85,
83, 77, 75, 50, 10, 5, 2, 1. Which is the
median?
A. 75 C. 76
B. 52.72 D. 77

49. What does a negatively skewed score contribution imply?
A. The scores congregate on the left or right side of the normal
distribution curve.
B. The students are academically poor.
C. A proportion of the class is academically poor.
D. The scores are widespread

50. Positively Skewed Distribution
Age Distribution
0
10
20
30
40
50
60
Age Groups
Frequency
Frequency 40 50 40 20 15 12
> 59 50 - 59 40 - 49 30 - 39 20 - 29 < 20

51. Positive Skewness
•Has pileup of cases to the left & the right tail of
distribution is too long

52. Negatively Skewed Distribution
Distribution of Scores on the Numerical Section of GRE
0
200
400
600
800
1000
1200
GRE - Numerical Scores
Frequency
Frequency 300 500 600 1000 1100 950
<100 100 - 199 200 - 299 300 - 399 400 - 499 500 - 600

53. Negative Skewness
•Has pileup of cases to the right & the left tail of
distribution is too long

54. Relative Locations for Measures of
Central Tendency
Negatively
Skewed
Mode
Median
Mean
Symmetric
(Not Skewed)
Mean
Median
Mode
Positively
Skewed
Mode
Median
Mean

55. The following table summarize the scores of Section A in the recent periodic
test in Chemistry. What is the median score interval?
SCORE FREQUENCY
94 – 97 2
90 – 93 4
86 – 89 6
82 – 85 13
78 – 81 3
74 – 77 3
70 – 73 6
A. 82 - 85 C. 86 - 89
B. 90 - 93 D. 78 – 81

56. SCORE FREQUENCY cf<
94 – 97 2 37
90 – 93 4 35
86 – 89 6 31
82 – 85 13 25
78 – 81 3 12
74 – 77 3 9
70 – 73 6 6
n = 37
Median = lb + (n/2 - cf<)i
f
= 81.5 + (18.5 - 12)4
13
= 81.5 + 8.7
= 90.2

57. Sources:
mathjourneys.com › slideshows › add_subt_fractions
www.logan.kyschools.us › multiply and divide fractions
www.msubillings.edu › asc › module_a › a_powerpoints
coppinacademy.org › auto › Volume-of-Prisms
www.bcsdschools.net › Centricity › Domain › 7.1.ppt
www.cobblearning.net › jonesa › files › 2016/02 ›The...