Downloaded 170 times
Uploaded byDivyansh Verma
LINEAR ALGEBRA BEHIND GOOGLE SEARCH
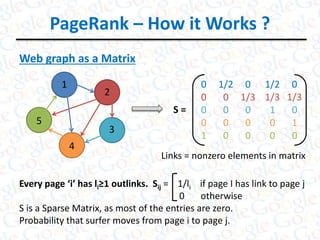
1) The document discusses how Google's PageRank algorithm uses concepts from linear algebra to rank the importance of web pages. 2) It explains that PageRank represents the web as a graph with pages as nodes and links as edges, which can be represented as a stochastic matrix. 3) The dominant eigenvector of this matrix gives the PageRank values that determine the order web pages are displayed in search results, with higher PageRank pages shown first.
More Related Content
Similar to LINEAR ALGEBRA BEHIND GOOGLE SEARCH
LINEAR ALGEBRA BEHIND GOOGLE SEARCH
- 1. Divyansh Verma SAU/AM(M)/2014/14 South AsianUniversity Email : itsmedv91@gmail.com LINEAR ALGEBRA BEHIND GOOGLE SEARCH
- 2. Contents • Search Engine: Google • Magic Behind Google Success • PageRank Algorithm • PageRank - How it works ? • Importance of Linear Algebra in Page Ranking Algorithm • References
- 3. Search Engine :Google What is a search engine? A web search engine is a software system that is designed to search for information on the World Wide Web. Eg : Google, Bing, Yahoo, Ask, etc. Why Google? • It is the most popular search engine. • It is very simple, fast and precise. • Adaptive to growing internet.
- 4. Magic Behind GoogleSuccess When Google went online in 1990’s, one thing that set it apart from other search engines was its search result listings which always delivered “good stuff”. Search Engines like Google have to do three basic things : 1. Look the web and locate all web pages with public access. 2. Indexing of searched data for more efficient search. 3. Rate the importance of each page in the database, so when the user does a search, the more important pages are presented first. Big part of the MAGIC behind Google success is its PageRank Algorithm.
- 5. PageRank Algorithm PageRank Algorithm,developed by Google’s founders, Larry Page and Sergey Brin, when they were graduate students at Stanford University. PageRank is a link analysis algorithm that ranks the relative importance of all web pages within a network. Three features for determining PageRank : • Outgoing Links - the number of links found in a page • Incoming Links - the number of times other pages have cited this page • Rank - A value representing the page's relative importance in the network.
- 6. PageRank – Howit Works ? Mathematical Model of Internet 1. Represent Internet as Graph 2. Represent Graph as Stochastic Matrix 3. Make stochastic matrix more convenient ⇒ Google Matrix 4. Find Dominant eigenvector of Google Matrix ⇒ PageRank Internet as a Graph Link from one web page to another web page. Web graph : Web pages = nodes, Links = edges
- 7. PageRank – Howit Works ? Web graph as a Matrix Links = nonzero elements in matrix Every page ‘i’ has li≥1 outlinks. Sij = 1/li if page I has link to page j 0 otherwise S is a Sparse Matrix, as most of the entries are zero. Probability that surfer moves from page i to page j. 1 2 3 4 5 S = 0 1/2 0 1/2 0 0 0 1/3 1/3 1/3 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0
- 8. PageRank – Howit Works ? Google Matrix Convex Combination of two Stochastic Matrix gives a Google Stochastic Matrix which is reducible and more convenient. G = αS + (1 − α)S1vT where 0≤ α ≤1 is damping factor, S1 is a matrix whose all entries are 1, vT is vector that models teleportation corresponding to webpage vi Eigen Values of G are 1 > α λ2(S) ≥ α λ3(S) ≥ . . . Unique dominant left eigenvector : πTG = πT, π ≥ 0 Links Teleportation
- 9. PageRank – Howit Works ? PageRank Dominant Eigen Vector πT gives PageRank corresponding webpage i πTG = πT, π ≥ 0 πi is the PageRank Corresponding to webpage i How Google Ranks Web pages • Model : Internet → Web Graph → Stochastic Matrix G • Computation : Dominant eigenvector of G for PageRank πi • Display : πi > πk , then page i may* be displayed before page k *depending on hypertext analysis
- 10. Importance of LinearAlgebra Using techniques of Linear Algebra, one can compute a unique solution for PageRank Problem. It gives importance of all webpages in terms of PageRank Eigenvector corresponding to each webpage. No other successful technique other than Linear Algebra is available to solve this problem.
- 11.
- 12.