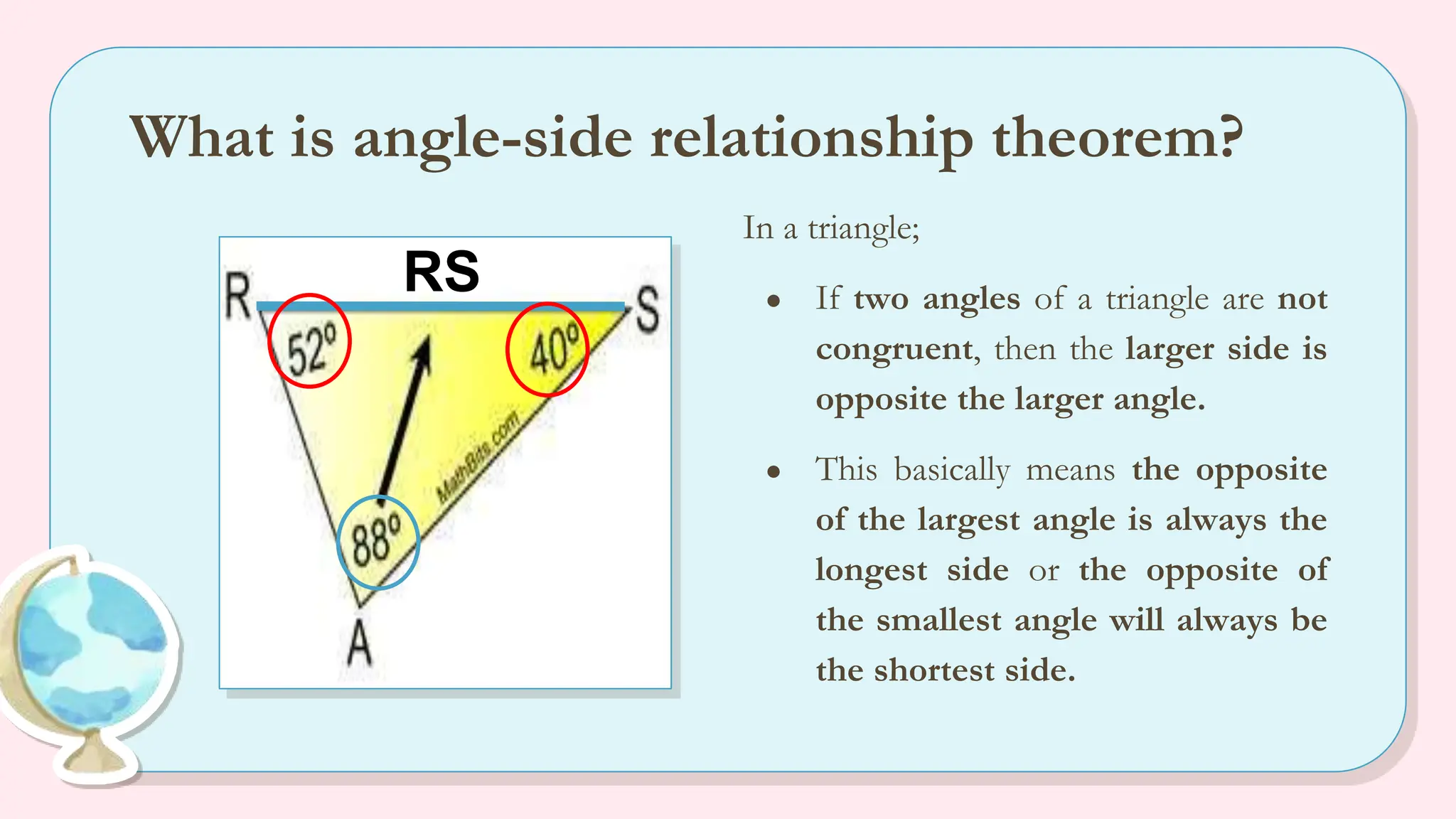
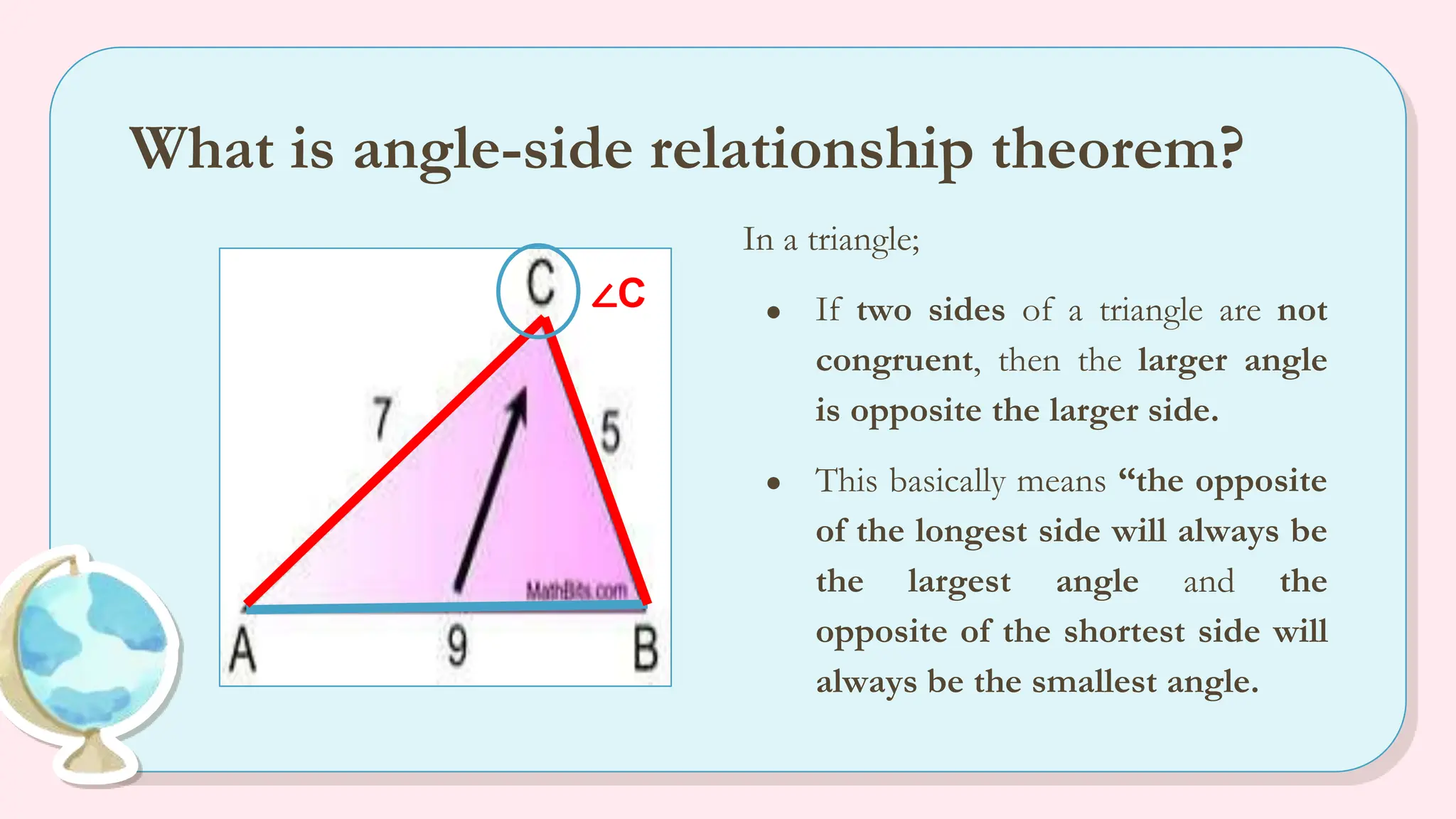
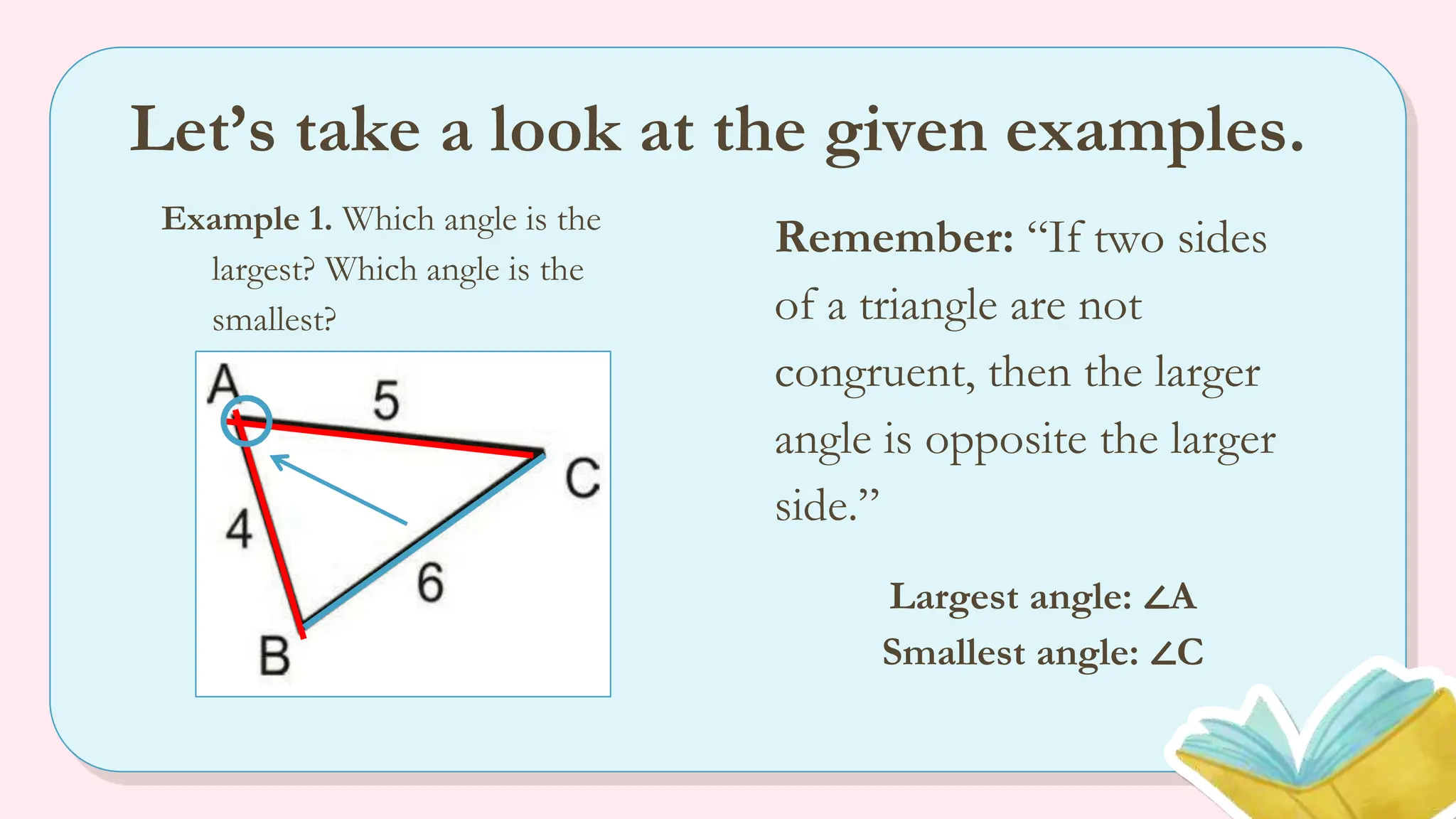
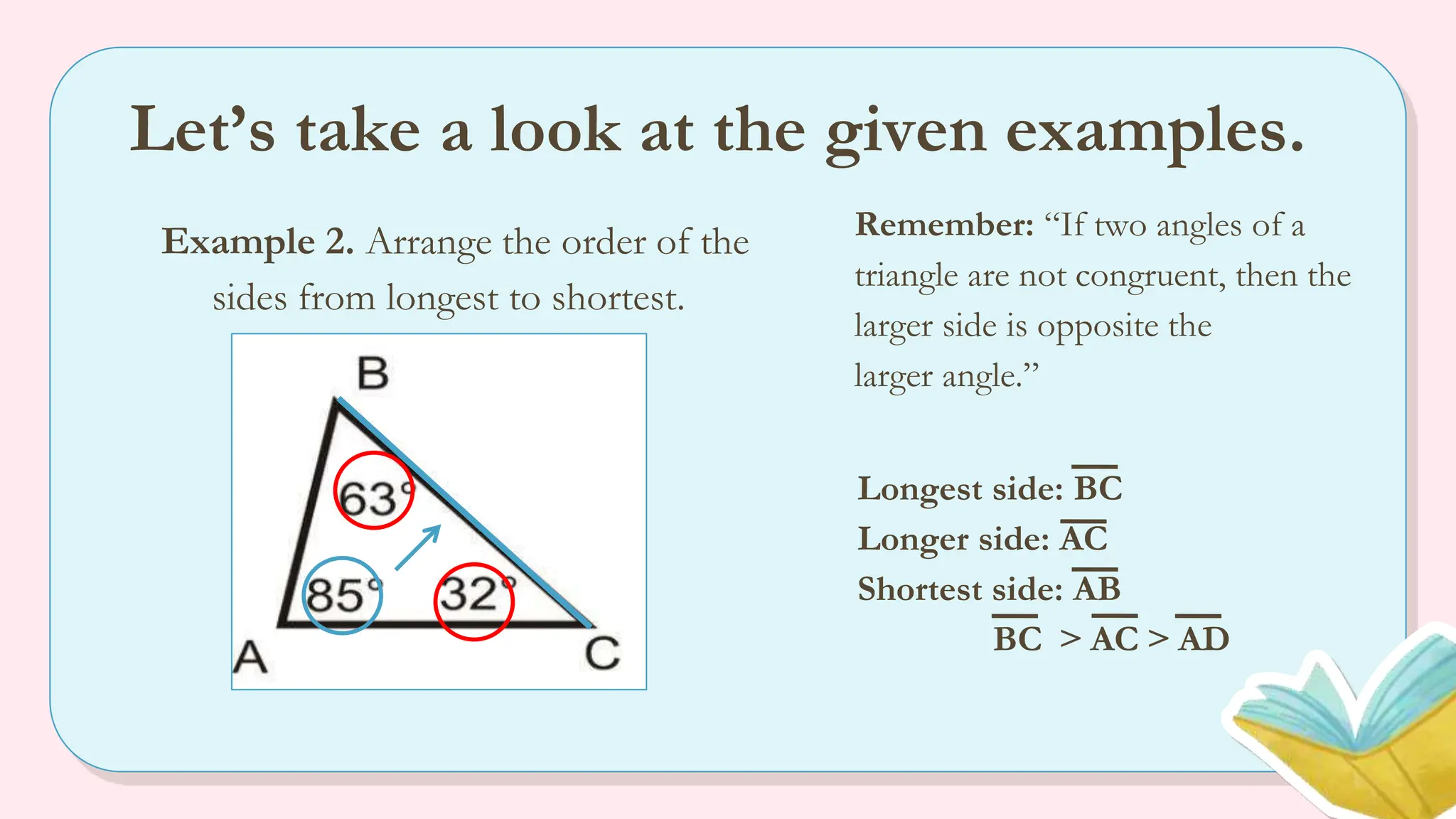
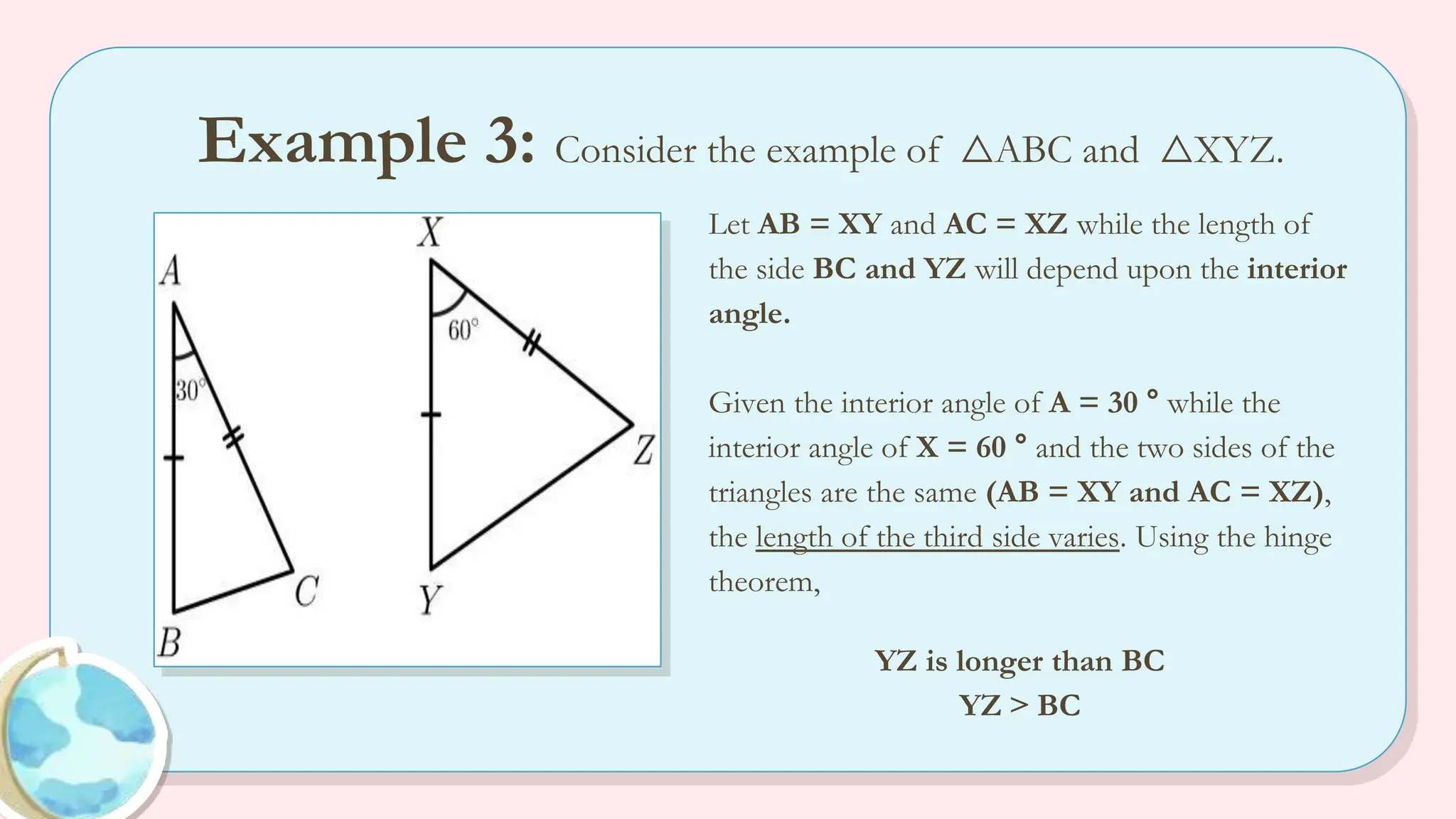
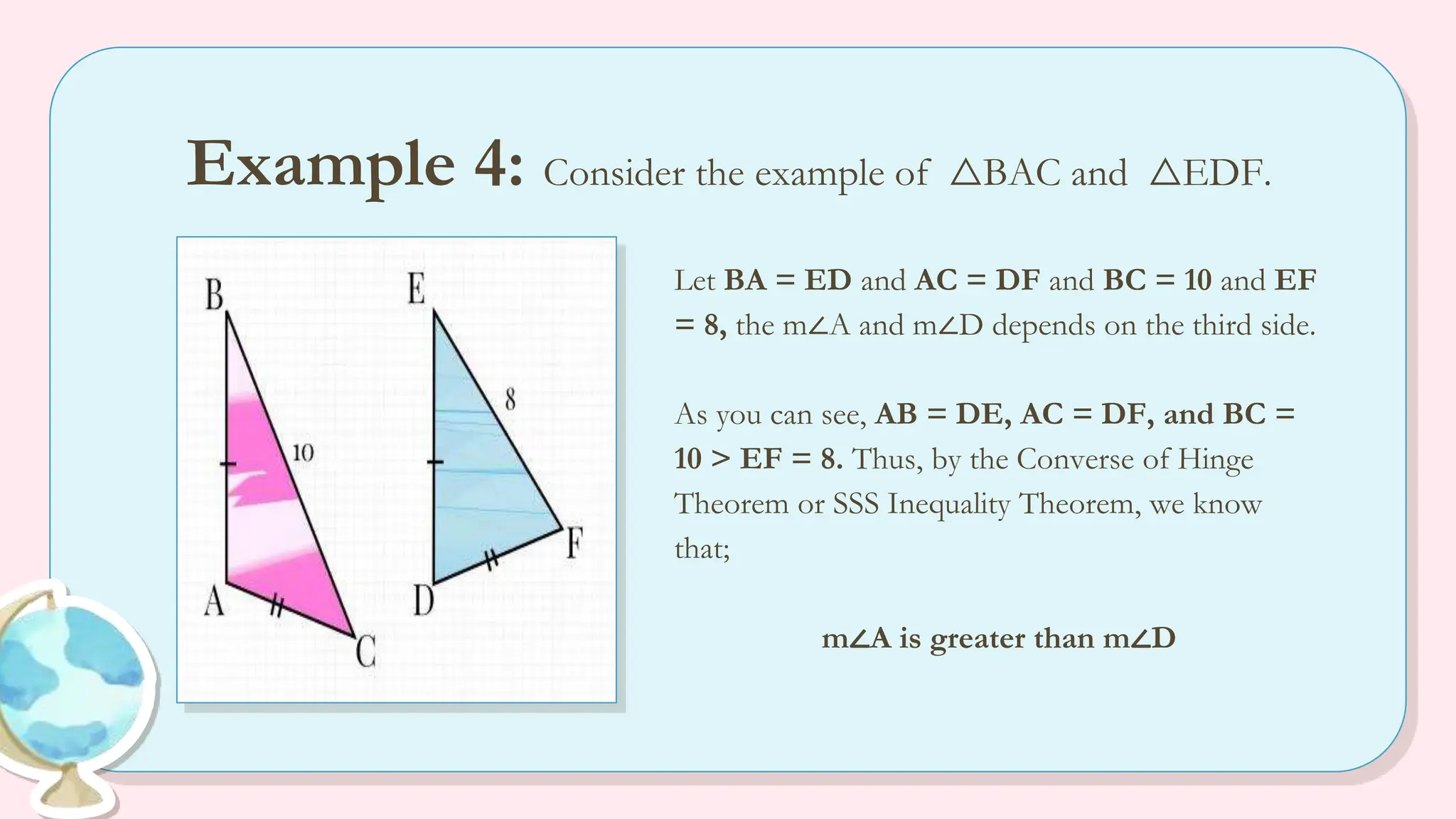
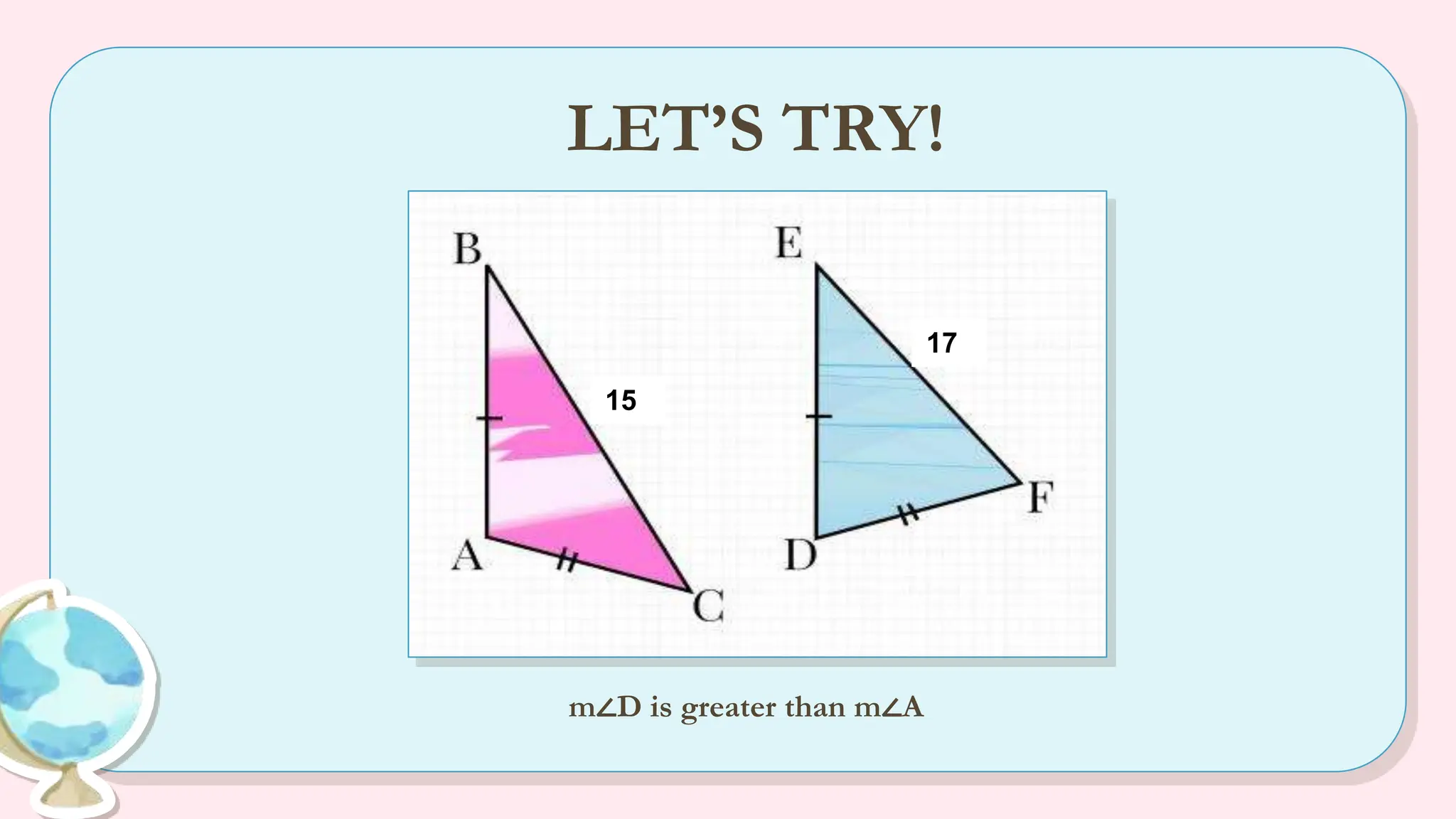
The document explains the angle-side relationship theorem, which states that in a triangle, the larger angle is opposite the longer side and vice versa. It also covers the hinge theorem, illustrating how two congruent sides and a greater included angle indicates a longer third side, and the converse hinge theorem, which states that a longer third side correlates with a larger included angle. Multiple examples are provided to clarify these concepts, along with links to informative videos.

1. Good day,
students!
8th Grade

2. Angle-side
Relationship
Theorem
8th Grade

3. What is angle-side relationship theorem?
In a triangle;
● If two angles of a triangle are not
congruent, then the larger side is
opposite the larger angle.
● This basically means the opposite
of the largest angle is always the
longest side or the opposite of
the smallest angle will always be
the shortest side.
RS

4. What is angle-side relationship theorem?
In a triangle;
● If two sides of a triangle are not
congruent, then the larger angle
is opposite the larger side.
● This basically means “the opposite
of the longest side will always be
the largest angle and the
opposite of the shortest side will
always be the smallest angle.
∠C

5. Let’s take a look at the given examples.
Remember: “If two sides
of a triangle are not
congruent, then the larger
angle is opposite the larger
side.”
Example 1. Which angle is the
largest? Which angle is the
smallest?
Largest angle: ∠A
Smallest angle: ∠C

6. Let’s take a look at the given examples.
Remember: “If two angles of a
triangle are not congruent, then the
larger side is opposite the
larger angle.”
Example 2. Arrange the order of the
sides from longest to shortest.
Longest side: BC
Longer side: AC
Shortest side: AB
BC ˃ AC ˃ AD

7. 8th Grade
To fully understand angle-side relationship theorem, let’s
watch this video:
Link: https://www.youtube.com/watch?v=4ME9ms1nPtU

8. Hinge
Theorem
8th Grade
(SAS Inequality Theorem)

9. What is hinge theorem?
● If two sides of one triangle are congruent to two sides of
another triangle, but the included angle of the first triangle is
greater than the included angle of the second, then the third
side of the first triangle is longer than the third side of the
second.
● So in short, the triangle having a larger interior angle will
also have a longer third side.

10. Example 3: Consider the example of △ABC and △XYZ.
Let AB = XY and AC = XZ while the length of
the side BC and YZ will depend upon the interior
angle.
Given the interior angle of A = 30 ° while the
interior angle of X = 60 ° and the two sides of the
triangles are the same (AB = XY and AC = XZ),
the length of the third side varies. Using the hinge
theorem,
YZ is longer than BC
YZ ˃ BC

11. LET’S TRY!
YZ is longer than BC
YZ ˃ BC
55 °
78 °

12. 8th Grade
To fully understand hinge and converse of hinge theorem,
let’s watch this video:
Link: https://www.youtube.com/watch?v=-mGDz9tZP2g

13. Converse of
Hinge Theorem
8th Grade
(SSS Inequality Theorem)

14. What is converse hinge theorem?
● If two sides of one triangle are congruent to two sides of
another triangle, but the third side of the first triangle is
longer than the third side of the second, then the included
angle of the first triangle is larger than the included angle of
the second.
● So in short, the triangle having the longer third side will also
have a larger included angle.

15. Example 4: Consider the example of △BAC and △EDF.
Let BA = ED and AC = DF and BC = 10 and EF
= 8, the m∠A and m∠D depends on the third side.
As you can see, AB = DE, AC = DF, and BC =
10 > EF = 8. Thus, by the Converse of Hinge
Theorem or SSS Inequality Theorem, we know
that;
m∠A is greater than m∠D

16. LET’S TRY!
m∠D is greater than m∠A
15
17

17. Let’s take a look at the given examples.
Given: 1st side: SR = NL; 2nd side:
ST = ML; included angles: ∠ S =
54°; and ∠ L = 71°
Find: Which third side is longer? Is
it RT or NM?
Example 5. Complete the statement
with >, ∠ or =. Determine what
theorem is used.
RT ____ NM
_____________
>
Hinge Theorem
Since m ∠ L > m ∠ S, therefore by
Hinge Theorem,
RT > NM

18. Let’s take a look at the given examples.
Given: 1st sides: TS = TO; 2nd
sides: TP = TP; third sides: PS =
16 cm and PO = 11 cm
Find: Which included angle is
largest?
Example 6. Complete the statement
with >, ∠ or =. Determine what
theorem is used.
m∠STP _____ m∠OTP
_____________________
>
Converse of Hinge Theorem
Since PS > PO, therefore by
Converse of Hinge Theorem,
∠STP > ∠OTP

19. 8th Grade
To fully understand converse of hinge theorem, let’s
watch this video:
Link: https://www.youtube.com/watch?v=OG0QWelNBPw

20. 8th Grade
To fully understand converse of hinge theorem, let’s
watch this video:
Link: https://www.youtube.com/watch?v=eWotAj7wvpo

21. “Mathematics is not just about
numbers, equations, computations
or algorithms: it is about
UNDERSTANDING.”
—William Paul Thurston

22. Riza Mae Bayo
PREPARED BY:
MATH 8- Practice Teacher

23. CREDITS: This presentation template was created by Slidesgo, and
includes icons by Flaticon, and infographics & images by Freepik
Thanks!
Do you have any questions? You can
contact me through:
zarimae22@gmail.com
+639 611 925 220
RIZA MAE BAYO