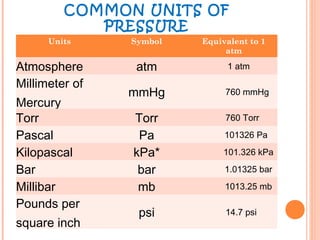
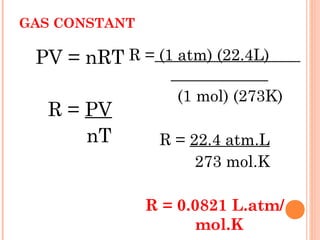
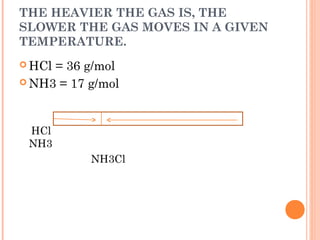
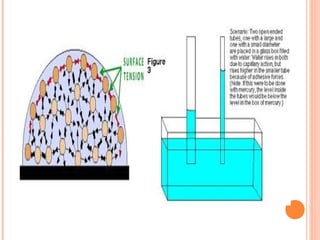
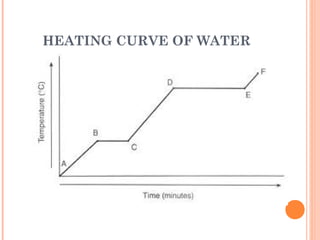
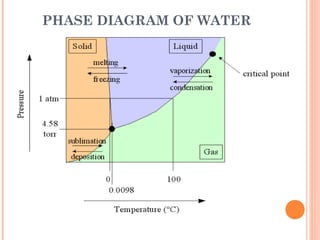
The document discusses the properties and behavior of gases, liquids, and solids from a microscopic perspective. It explains that gases have particles with empty space between them allowing the particles to move freely, while liquids have particles close together allowing them to flow but slide past one another, and solids have particles locked in a fixed structure. The document also covers gas laws, phase changes, types of solids based on bonding, and heating curves. It provides a concise overview of the states of matter and changes between states from a molecular level.

1. GASES

2. PROPERTIES
OF GASES

3. Gases are compressible.
Gases fill any container that
they occupy.
Gases expand in the heat.
Gases do not settle in their
container.

4. KINETIC MOLECULAR
THEORY OF GASES
 A gas consists of very small particles. The
particles are in constant, random,
straight-line motion.
 The molecules of a gas are very far from
each other relative to their size.
 There is no interaction between molecules,
they act independently of each other.
 Molecules collide with each other and with
the walls of the container in a perfectly
elastic manner.

5. PRESSURE
= force exerted per
unit area
P = F/A = N/m2
= Pa
= Blaise Pascal

6. COMMON UNITS OF
PRESSURE
Units Symbol Equivalent to 1
atm
Atmosphere atm 1 atm
Millimeter of
Mercury
mmHg 760 mmHg
Torr Torr 760 Torr
Pascal Pa 101326 Pa
Kilopascal kPa* 101.326 kPa
Bar bar 1.01325 bar
Millibar mb 1013.25 mb
Pounds per
square inch
psi 14.7 psi

7. EVANGELISTA
TORRICELLI

8. TEMPERATUR
E
-William Thomson/ Lord Kelvin
-
0 K = - 273 0
C
- K = 0
C + 273

9. STP/ STANDARD TEMPERATURE
AND PRESSURE
0 0
C 1 atm
760 mm Hg
760 torr

10. GAS
LAWS

11. Boyle’s
Law
Gay-
Lussac’s
Law
Dalton’s
Law of
Partial
Pressure
Charles’
Law
Avogadro’s
Law
Grahams
Law of
Effusion
Combined
Gas Law
Ideal Gas
Law

12. BOYLE’S LAW
- Robert Boyle
P ά 1/V
P1V1 = P2V2
Constant Variable:
T, n

13. A TANK OF NITROGEN HAS A
VOLUME OF 14.0 L AND A PRESSURE OF
760 MM HG. FIND THE VOLUME OF THE
NITROGEN WHEN ITS PRESSURE IS
CHANGED TO 400 MM HG WHILE THE
TEMPERATURE IS HELD CONSTANT.
Given:
V1 = 14 L
P1 = 760 mm Hg
P2 = 400 mm Hg
V2 = ?
Equation:
P1V1 = P2V2
V2 = P1V1
P2
V2 = 760 mm Hg(14 L)
400 mm Hg
V2 = 26.6 L

14. APPLICATIONS OF BOYLE’S
LAW
Breathing Syringe

15. APPLICATIONS OF BOYLE’S
LAW
Soda Can Scuba Diving

16. CHARLES’ LAW
Jacques Charles
V ά T
V1/T1 = V2/T2
Constant Variable:
P, n

17. A BALLOON HAS A VOLUME OF
2500 ML ON A DAY WHEN THE
TEMPERATURE IS 30 0
C. IF THE
TEMPERATURE AT NIGHT FALLS TO 10
0
C, WHAT WILL BE THE VOLUME OF THE
BALLOON IF THE PRESSURE REMAINS
CONSTANT?
Given:
T1 = 30 0
C = 303 K
T2 = 10 0
C = 283 K
V1 = 2500 ml
V2 = ?
Equation:
V1 = V2
T1 = T2
V2 = V1T2
T1
V2 = (2500 ml)(283K)
303 K
V2 = 2, 335 mL

18. APPLICATIONS OF CHARLES’
LAW

19. COMBINED GAS
LAW
= describes the
relationship among the
pressure, volume and
temperature at a
constant amount of gas
= Boyle’s Law and
Charles’ Law

20. COMBINED GAS LAW
Boyle’s Law
P ά 1/V
P1V1 = P2V2
Charles’ Law
V ά T
V1/T1 = V2/T2
V ά T/P
P1V1 = P2V2
T1 T2
Constant: n

21. A GIVEN MASS OF GAS HAS A
VOLUME OF 800 ML AT -23 0
C AND 300
TORR. WHAT WOULD BE THE VOLUME
OF THE GAS AT 27 0
C AND 600 TORR OF
PRESSURE? THE AMOUNT OF GAS S
CONSTANT.
Given:
V1 = 800 mL
T1= -23 0
C = 250 K
P1 = 300 torr
T2 = 27 0
C = 300 K
P2 = 600 torr
V2 = ?
P1V1 = P2V2
T1 T2
V2 = P1V1T2
P2T1
V2 =(300 torr)(800 mL)(300 K)
(600 torr)(250 K)
V2 = 480 mL

22. APPLICATIONS OF COMBINED
GAS LAW
This law gives us an insight on
how gases and volatile liquids
should be stored.
Gas tanks containing LPG inside
the container should be stored in
cool places to prevent the build-
up of a high pressure esp. if the
gas is flammable.

23. GAY- LUSSAC’S LAW
Joseph Louis Gay-
Lussac
P ά T
P1/T1 = P2/T2
Constant: V, n

24. A 2 L FLASKS CONTAINS HELIUM
GAS AT A PRESSURE OF 685 TORR AND A
TEMPERATURE OF 0 0
C. WHAT WOULD
BE THE PRESSURE IN THE FLASK IF
THE TEMPERATURE IS INCREASED TO
150 0
C?
Given:
P1 = 685 torr
T1 = 0 0
C = 273 K
T2 = 150 0
C = 423 K
P2 = ?
Equation:
P1 = P2
T1 T2
P2 = P1T2
T1
P2 = (685 torr)(423 K)
273 K
P2 = 1, 061 torr

25. APPLICATIONS OF GAY-
LUSSAC’S LAW
Pressure
Cooker

26. AVOGADRO’S LAW
Amedeo Avogadro
V ά n
V1/n1 = V2/n2
Constant: P, T

27. IF 0.25 MOL OF ARGON GAS
OCCUPIES A VOLUME OF 76.2 ML AT A
PARTICULAR TEMPERATURE AND
PRESSURE, WHAT VOLUME WOULD 0.43
MOL OF ARGON HAVE UNDER THE
SAME CONDITIONS?
Given:
n1 = 0.25 mol
n2 = 0.43 mol
V1 = 76.2 mL
V2 = ?
Equation:
V1 = V2
n1 n2
V2 = V1n2
n1
V2 = (76.2 mL)(0.43 mol)
0.25 mol
V2 = 131 mL

28. APPLICATIONS OF AVOGADRO’S
LAW
Inflating a balloon Breathing

29. IDEAL GAS LAW
Boyle’s Law
Charles’s Law
Avogadro’s
Law
Gay – Lussac’s
Law
Ideal Gas Equation:
V ά nT/P
PV = nRt
R (gas
constant)
= 0.0821 L. atm
mol. K

30. GAS CONSTANT
PV = nRT
R = PV
nT
R = (1 atm) (22.4L)
(1 mol) (273K)
R = 22.4 atm.L
273 mol.K
R = 0.0821 L.atm/
mol.K

31. WHAT VOLUME WILL 1.27 MOL OF
HELIUM GAS OCCUPY AT STP?
Given:
n= 1.27 mol
P = 1 atm
T = 273 K
R = 0.0821 L.atm
mol.K
V = ?
Equation:
PV = nRT
V = nRT
P
V =(1.27mol)(0.0821L.atm/mol.K)(273K)
1 atm
V = 28.5 L

32. APPLICATIONS OF IDEAL GAS
LAW
 Mountain climbers
often carry oxygen
tanks with them. The
air at these higher
altitudes is at lower
atmospheric pressure
or is ``thinner.'' This
phenomenon in which
pressure decreases
with increasing
altitude occurs in all
fluids.

33. DALTON’S LAW OF PARTIAL
PRESSURE
Partial Pressure
- the pressure each gas
would exert at the
same temp. and at the
same volume.
Ptotal = PA + PB + PC
+……Pn

34. GASES, OXGEN, CO2, AND HELIUM. THE
PARTIAL PRESSURES OF THE THREE
GASES ARE 2 ATM, 3 ATM AND 4 ATM
RESPECTIVELY. WHAT IS THE TOTAL
PRESSURE INSIDE THE CONTAINER?
Given:
PA = 2 atm
PB = 3 atm
PC = 4 atm
Ptotal = ?
Equation:
Ptotal = PA + PB + PC
Ptotal = 2 atm+ 3 atm+ 4 atm
Ptotal = 9 atm

35. IN A CLOSED SYSTEM, THE CHAMBER IS
PRESSURIZED TO 1200 TORR. IF THE
CHAMBER HOLDS 3 MOLES OF N2, 2
MOLES OF O2 AND 1 MOLE OF F2, WHAT
IS THE PRESSURE OF EACH GAS?
P total = 3 P1+ 2P2 + 1P3
1200 torr = 6P
P = 1200 torr/6 = 200 torr
N2 = 3 (2oo torr) = 600 torr
O2 = 2 (200 torr) = 400 torr
F2 = 1 (200 torr) = 200 torr
1200 torr

36.  The mixing of
gases due to
molecular motion
 The particles of gas
spread out
-Passage of molecules
of a gas from one
container to another
through a higher
pressure;
- Particles of gas
passing through a
small opening
Diffusion Effusion

37. GRAHAM’S LAW OF
EFFUSION
Thomas Graham
- the rate of effusion
of gas is inversely
proportional to the
square root of its
molar mass.
VB = √MWA
VA √MWB

38. HOW MUCH FASTER DOES O2 ESCAPE
THROUGH A POROUS CONTAINER THAN
SO2 UNDER SIMILAR CONDITION OF
TEMPERATURE AND PRESSURE?
Given:
MW O2 = 32g/mol
MW SO2 = 64g/mol
√MWSO2 = V O2
√MW O2 = V SO2
V O2 = √MWSO2
VSO2 = √MW O2
V1 = √64 g/mol
V2 √32 g/mol
= 8/5.66
= 1.41
This means that O2 diffuses
1.41 times as fast as SO2

39. THE HEAVIER THE GAS IS, THE
SLOWER THE GAS MOVES IN A GIVEN
TEMPERATURE.
 HCl = 36 g/mol
 NH3 = 17 g/mol
HCl
NH3
NH3Cl

40. CONDENSED
STATES OF
MATTER
Solids and Liquids
- states in which the atoms or
molecules are fairly close
together and their behavior is
determined (at least in part)
by the attractions between
them.

41. Some Characteristics of Gases, Liquids and Solids and the Microscopic
Explanation for the Behavior
gas liquid solid
assumes the shape and
volume of its container
particles can move past
one another
assumes the shape of the
part of the container
which it occupies
particles can move/slide
past one another
retains a fixed volume
and shape
rigid - particles locked
into place
compressible
lots of free space
between particles
not easily compressible
little free space between
particles
not easily compressible
little free space between
particles
flows easily
particles can move past
one another
flows easily
particles can move/slide
past one another
does not flow easily
rigid - particles cannot
move/slide past one
another

42. PROPERTIES OF
LIQUID
Evaporation
Vapor Pressure
Boiling Point
Surface Tension
Capillary Action

44. TYPES OF SOLIDS
Vitreous or
Amorphous Solids
- shapeless solids; solids
that do not have
definite melting
points; its particles do
not have an orderly
arrangement; their
arrangement is
random similar to
liquids.

45. CRYSTALLINE SOLIDS
solids that
have definite
melting point
like NaCl and
sugar; they
have an
orderly
arrangement
of particles.

46. ALLOTROPES
crystalline solids
that exist in
various forms
like carbon, it
can exist as
diamond and
graphite.

47. Covalent Ionic Metallic Molecular
Particles that
occupy the
lattice sites
Atoms Positive and
Negative ions
Metal atoms Molecules
Nature of
bonding
Electron
Sharing
Electrostatic
attraction
Electrical
attraction
between the
outer level
electron and
the nuclei
Van der Waals
forces
Properties They are hard,
nonvolatile, and
have high
melting point.
They are good
insulators.
They are quite
hard and brittle.
They have
fairly high
melting points
and are good
insulators.
They have
variable melting
points and
hardness. They
are good
conductors of
electricity.
They are
generally soft
and have low
melting points.
They are good
insulators.
Examples Diamond,
carborundum,
quartz
Sodium
chloride,
potassium
nitrate, sodium
sulfate
Copper, iron,
aluminum
Ice, dry ice,
sucrose, iodine
Properties of Solids Based on the Type of Bonding

48. Process Phase Change Direction of Movement of
Heat
From To
Melting (fusion) Solid Liquid Heat goes into the solid as it
melts.
Freezing(Solidification) Liquid Solid Heat leaves the liquid as it
freezes.
Vaporization Liquid Gas Heat goes into the liquid as it
vaporizes.
Condensation Gas Liquid Heat leaves the gas as it
condenses.
Sublimation Solid Gas Heat goes into the solid as it
sublimes.
Deposition Gas Solid Heat leaves the gas as it
solidifies.
PHASE CHANGES- occur by either the absorption or release of energy
usually in the form of heat.
Heat Movement During Phase Change

49. HEATING CURVE OF WATER

50. PHASE DIAGRAM OF WATER

51. THANK YOU
VERY
MUCH!!!
Prepared by:
Divina Michelle B. Belcina