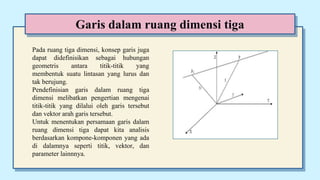
Dokumen ini membahas tentang persamaan garis dalam ruang tiga dimensi, termasuk persamaan vektor garis, persamaan parametrik garis, dan persamaan simetrik garis. Selain itu, dibahas pula kedudukan dua garis dalam ruang tiga dimensi dan hubungannya dengan bidang datar."

1. PERSAMAAN GARIS
DALAM RUANG
DIMENSI TIGA
Dosen Pengampu :
Dr. Nyoman Sridana, M.Si
NI Made Intan Kertiyani, S.Pd.,M.Pd

2. 01
Anggota Kelompok 3:
Hanifa Zahrani
(E1R021135)
02 Silvana Kurniawati
(E1R021103)
03
Didi Firmansyah
(E1R021053 )

3. Kedudukan Garis Dalam Ruang Dimensi Tiga
01 Garis Dalam Ruang Dimensi Tiga
Pembahasan Masalah
Contoh Soal
02
03

4. Garis Dalam Ruang
Dimensi Tiga
01

5. Garis dalam ruang dimensi tiga
Pada ruang tiga dimensi, konsep garis juga
dapat didefinisikan sebagai hubungan
geometris antara titik-titik yang
membentuk suatu lintasan yang lurus dan
tak berujung.
Pendefinisian garis dalam ruang tiga
dimensi melibatkan pengertian mengenai
titik-titik yang dilalui oleh garis tersebut
dan vektor arah garis tersebut.
Untuk menentukan persamaan garis dalam
ruang dimensi tiga dapat kita analisis
berdasarkan kompone-komponen yang ada
di dalamnya seperti titik, vektor, dan
parameter lainnnya.

6. Persamaan vektor garis ℓ
Persamaan Garis Dalam Ruang Dimensi Tiga
Persamaan vektor garis adalah representasi matematis dari suatu garis dalam ruang
tiga dimensi menggunakan vektor. Dalam persamaan ini, vektor arah garis dan titik
yang dilewati oleh garis dinyatakan dengan menggunakan parameter. Persamaan
ini memungkinkan kita untuk mengidentifikasi setiap titik pada garis dengan
menggunakan nilai parameter tertentu.

7.  Titik 𝑃0 𝑥0, 𝑦0, 𝑧0 pada garis 𝓁
 Garis 𝓁 sejajar dengan vektor 𝑣 = 𝑎𝑖 + 𝑏𝑗 + 𝑐𝑘
 Ambil sebarang titik 𝑃 𝑥, 𝑦, 𝑧 pada garis 𝓁 maka
𝑃0𝑃 = 𝑡𝑣 dengan 𝑡 bilangan real (𝑃0𝑃‖ 𝑣)
 Vektor-vektor posisi titik 𝑃0 dan 𝑃 terhadap 𝑂 adalah
𝑟0 = 𝑥0, 𝑦0, 𝑧0 dan 𝑟 = 𝑥, 𝑦, 𝑧 maka 𝑃0𝑃 = 𝑟 − 𝑟0 dan
karena 𝑃0𝑃 = 𝑡𝑣 maka:
𝒓 − 𝒓𝟎 = 𝒕𝒗
𝒓 = 𝒓𝟎 + 𝒕𝒗

8. Persamaan parametik garis ℓ
Dalam persamaan parametrik, setiap koordinat titik pada garis dinyatakan sebagai fungsi
dari satu atau lebih parameter.
〈𝑥, 𝑦, 𝑧〉 = 〈𝑥0, 𝑦0, 𝑧0〉 + 𝑡⟨𝑎, 𝑏, 𝑐⟩
atau
〈𝑥, 𝑦, 𝑧〉 = 〈𝑥0 + 𝑡𝑎, 𝑦0 + 𝑡𝑏, 𝑧0 + 𝑡𝑐〉
Jadi,
𝒙 = 𝒙𝟎 + 𝒕𝒂;
𝒚 = 𝒚𝟎 + 𝒕𝒃;
𝒛 = 𝒛𝟎 + 𝒕𝒄
(persamaan ini disebut persamaan parametrik dari garis 𝑃)

9. Persamaan simetrik garis sering diekspresikan dalam bentuk persamaan
parametrik dan digunakan untuk menggambarkan garis secara lebih sederhana.
Apabila parameter 𝑡 dari persamaan parametrik dihilangkan, maka diperoleh:
𝒙 − 𝒙𝟎
𝒂
=
𝒚 − 𝒚𝟎
𝒃
=
𝒛 − 𝒛𝟎
𝒄
Disebut persamaan simetrik dari garis 𝓁 dengan bilangan arah 𝑎, 𝑏, 𝑐 dan
melalui titik 𝑥0, 𝑦0, 𝑧0 .
Persamaan simetrik garis ℓ

10. Jika terdapat titik 𝐴 𝑥1, 𝑦1, 𝑧1 dan titik 𝐵 𝑥2, 𝑦2, 𝑧2 .
Maka dapat ditentukan bentuk persamaan vektor garis 𝐴𝐵 sebagai berikut:
𝑟 = 𝑎 + 𝑡 𝑏 − 𝑎 dengan 𝑡 bilangan real
𝑥, 𝑦, 𝑧 = 𝑥1, 𝑦1, 𝑧1 + 𝑡 𝑥2 − 𝑥1, 𝑦2 − 𝑦1, 𝑧2 − 𝑧1
𝒙 = 𝒙𝟏 + 𝒕 𝒙𝟐 − 𝒙𝟏 , 𝒚 = 𝒚𝟏 + 𝒕 𝒚𝟐 − 𝒚𝟏 , 𝒛 = 𝒛𝟏 + 𝒕 𝒛𝟐 − 𝒛𝟏
Dengan melenyapkan parameter 𝑡 dari persamaan parametrik ini, akan diperoleh persamaan simetrik
dari garis 𝐴𝐵 sebagai berikut:
𝒙 − 𝒙𝟏
𝒙𝟐 − 𝒙𝟏
=
𝒚 − 𝒚𝟏
𝒚𝟐 − 𝒚𝟏
=
𝒛 − 𝒛𝟏
𝒛𝟐 − 𝒛𝟏
Persamaan garis lurus yang melalui 𝐴 𝑥1, 𝑦1, 𝑧1 dan titik 𝐵 𝑥2, 𝑦2, 𝑧2 .

11. Kedudukan Garis Dalam
Ruang Dimensi Tiga
02

12. Dua buah garis lurus dalam ruang kemungkinan akan berpotongan, sejajar, berhimpitan atau
bersilangan.
Misalkan diketahui dua garis berikut ini:
𝑥−𝑥1
𝑎1
=
𝑦−𝑦1
𝑏1
=
𝑧−𝑧1
𝑐1
atau
𝑥−𝑥2
𝑎2
=
𝑦−𝑦2
𝑏2
=
𝑧−𝑧2
𝑐2
sudut antara dua garis sama dengan sudut yang dibentuk oleh vektor - vektor arahnya, yaitu
𝑚1 = 𝑎1, 𝑏1, 𝑐1 dan 𝑚2 = 𝑎2, 𝑏2, 𝑐2 .
Jika θ adalah sudut yang dibentuk oleh dua garis tersebut, maka:
cos θ =
𝑎1𝑎2+ 𝑏1𝑏2+𝑐1𝑐2
𝑎1
2+𝑏1
2
+𝑐1
2 𝑎2
2+𝑏2
2
+𝑐2
2
Kedudukan dua garis dalam ruang dimensi tiga

13.  Dua garis akan sejajar, apabila vektor-vektor arahnya sejajar, yaitu 𝑚1 = 𝑡𝑚2 dengan
t suatu bilangan real 𝑎1, 𝑏1, 𝑐1 = t 𝑎2, 𝑏2, 𝑐2 atau
𝑎1
𝑎2
=
𝑏1
𝑏2
=
𝑐1
𝑐2
 Dua garis saling tegak lurus, apabila vektor-vektor arahnya saling tegak lurus, yaitu:
𝑚1. 𝑚2 = 0
𝑎1, 𝑏1, 𝑐1 . 𝑎2, 𝑏2, 𝑐2 = 0
𝑎1𝑎2 + 𝑏1𝑏2 + 𝑐1𝑐2 = 0

14.  Berhimpit, diketahui garis lurus :
𝑔1: 𝑥, 𝑦, 𝑧 = [ 𝑥1, 𝑦1, 𝑧1] + 𝜆[𝑎1, 𝑏1, 𝑐1] dan 𝑔2: 𝑥, 𝑦, 𝑧 = [ 𝑥2, 𝑦2, 𝑧2] + 𝜆[𝑎2, 𝑏2, 𝑐2]
Bila [𝑎1, 𝑏1, 𝑐1]= 𝜇 𝑎2, 𝑏2, 𝑐2 ; 𝜇 bilangan ≠ 0, atau bila
𝑎1
𝑎2
=
𝑏1
𝑏2
=
𝑐1
𝑐2
Bila sifat diatas berlaku pula 𝑥2 − 𝑥1, 𝑦2−𝑦1, 𝑧2 − 𝑧1 = 𝜇 𝑎1, 𝑏1, 𝑐1 maka 𝑔1dan 𝑔2 berhimpit.
 Berpotngan disatu titik atau bersilangan,
Jika arah 𝑔1 yaitu [𝑎1, 𝑏1, 𝑐1] dan arah 𝑔2 yaitu [𝑎2, 𝑏2, 𝑐2] tidak berkelipatan, maka 𝑔1dan 𝑔2 berpotngan disatu
titik atau bersilangan. Misalkan titik potong 𝑥0, 𝑦0, 𝑧0 berarti ada 𝜆1 sehingga 𝑥0, 𝑦0, 𝑧0 = [𝑥1, 𝑦1, 𝑧1] +
𝜆[𝑎1, 𝑏1, 𝑐1] dan ada 𝜆2 sehingga 𝑥0, 𝑦0, 𝑧0 = [𝑥2, 𝑦2, 𝑧2] + 𝜆[𝑎2, 𝑏2, 𝑐2] berarti :
[𝑥1, 𝑦1, 𝑧1] + 𝜆[𝑎1, 𝑏1, 𝑐1] = [𝑥2, 𝑦2, 𝑧2] + 𝜆[𝑎2, 𝑏2, 𝑐2]

15. Kedudukan garis terhadap bidang datar
Ada tiga kemungkinan yang terjadi, letak suatu garis terhadap suatu bidang datar, yaitu garis
memotong bidang, garis sejajar bidang dan garis terletak pada bidang.
Perhatikan sebuah garis 𝓁:
𝑥−𝑥1
𝑎
=
𝑦−𝑦1
𝑏
=
𝑧−𝑧1
𝑐
Dan sebuah bidang 𝑎 ∶ 𝐴𝑥 + 𝐵𝑦 + 𝐶𝑧 + 𝐷 = 0.
Diambil sembarang titik 𝑃(𝑥𝑝, 𝑦𝑝, 𝑧𝑝) misalkan garis dan bidang ini berpotongan,
maka koordinat titik potongnya dicari dengan menyelesaikan 𝑥𝑝, 𝑦𝑝, dan 𝑧𝑝 dari tiga
persamaan itu.

16. Salah satu cara menyelesaikannya dengan memisalkan bahwa
𝑥𝑝 − 𝑥1
𝑎
=
𝑦𝑝 − 𝑦1
𝑏
=
𝑧𝑝 − 𝑧1
𝑐
𝑥𝑝 = 𝑥1 + 𝑎𝑡, 𝑦𝑝 = 𝑦1 + 𝑏𝑡, 𝑧𝑝 = 𝑧1 + 𝑐𝑡 disubtitusikan pada persamaan bidang, maka diperoleh
𝐴 𝑥1 + 𝑎𝑡 + 𝐵 𝑦1 + 𝑏𝑡 + 𝐶 𝑧1 + 𝑐𝑡 + 𝐷 = 0
𝐴𝑎 + 𝐵𝑏 + 𝐶𝑐 𝑡 + 𝐴𝑥1 + 𝐵𝑦1 + 𝐶𝑧1 + 𝐷 = 0
Apabila 𝐴𝑎 + 𝐵𝑏 + 𝐶𝑐 ≠ 0, maka kita akan memperoleh nilai 𝑡, hingga koordinat titik potong garis
dan bidang diperoleh dengan mensubstitusikan nilai 𝑡 ke dalam perrsamaan garis yang memuat 𝑡

17.  Jika 𝐴𝑥1 + 𝐵𝑦1 + 𝐶𝑧1 + 𝐷 = 0 dan 𝐴𝑎 + 𝐵𝑏 + 𝐶𝑐 ≠ 0, maka titik potong garis dan bidang itu
adalah 𝑥1, 𝑦1, 𝑧1 .
 Jika 𝐴𝑎 + 𝐵𝑏 + 𝐶𝑐 = 0, dan 𝐴𝑥1 + 𝐵𝑦1 + 𝐶𝑧1 + 𝐷 ≠ 0, maka garis dan bidang akan sejajar.
 Garis tegak lurus pada bidang apabila 𝑚 = 𝑘𝑛, dengan 𝑘 bilangan real atau
𝑎
𝐴
=
𝑏
𝐵
=
𝑐
𝐶
 Jika 𝐴𝑎 + 𝐵𝑏 + 𝐶𝑐 = 0 dan 𝐴𝑥1 + 𝐵𝑦1 + 𝐶𝑧1 + 𝐷 = 0, maka garis terletak pada bidang. Atau
jika 𝑚 . 𝑛 = 0 maka 𝑚  𝑛, sehingga garis sejajar dengan bidang. Artinya garis terletak
seluruhnya pada bidang.

18. Jarak dua Garis Bersilangan
Misalkan diketahui dua garis bersilan
𝑔1: 𝑥, 𝑦, 𝑧 = 𝑥1, 𝑦1, 𝑧1 + 𝑎1, 𝑏1, 𝑐1 dan 𝑔2: 𝑥, 𝑦, 𝑧 = 𝑥2, 𝑦2, 𝑧2 + 𝑎2, 𝑏2, 𝑐2
Jarak garis 𝑔1 dan 𝑔2 ditentukan dengan cara membuat
bidang α melalui garis 𝑔2 dan sejajar garis 𝑔1. Pilih suatu
titik T pada garis 𝑔1. Maka jarak garis 𝑔1 dan 𝑔2 adalah
jarak titik T ke bidang α.
Rumus jarak garis ke bidang:
𝑑 =
𝐴 𝑥2 − 𝐵 𝑦2 + 𝐶 𝑧2 + 𝐷
𝐴2 + 𝐵2 + 𝐶2

19. Contoh Soal
03

20. Contoh Soal 1
Berapakah jarak garis 𝑔1 ∶ 7𝑥 − 4𝑧 − 38 = 0 , 7𝑦 − 5𝑧 + 37 = 0 dan garis 𝑔2 ∶ 7x + 8z − 16 = 0,
7y − 3z = 15
Jawab:
Persamaan bidang yang melalui garis 𝑔1 adalah anggota berkas bidang (7𝑥 − 4𝑧 − 38) + 𝑡 (7𝑦 − 5𝑧 +
37) = 0 atau 7𝑥 + 7𝑡𝑦 + 4 − 5𝑡 𝑧 − 38 + 37𝑡 = 0.
Vektor normal bidang ini adalah 𝑛 = 7, 7𝑡, 4 − 5𝑡 .
Sedangkan vektor arah garis 𝑔2 adalah:
𝑚 =
0 8
7 −3
, −
7 8
0 −3
,
7 0
0 7
= −56, 21, 49

21. Bidang yang melalui 𝑔1 sejajar dengan 𝑔2, maka harus dipenuhi:
𝑚 ⊥ 𝑛, yaitu 𝑚 . 𝑛 = 0 ⇒ −56,21, 49 . 7, 7𝑡, 4 − 5 = 0
-8 + 3t + 4 – 5t = 0
t = -2
Jadi bidang yang melalui 𝑔1 sejajar dengan 𝑔2 adalah 7𝑥 − 14𝑦 + 14𝑧 − 112 = 0 yang
disederhanakan menjadi 𝑥 − 2𝑦 + 2𝑦 – 16 = 0. Pilih titik P(0,3,2) pada garis 𝑔2, maka jarak P
ke bidang 𝑥 − 2𝑦 + 2𝑦 − 16 = 0 adalah:
𝑑 =
0 − 2.3 + 2.2 − 16
1 + 4 + 4
= 6
Jadi, jarak garis-garis 𝑔1 dan 𝑔2 adalah 6 satuan Panjang.

22. Contoh Soal
1. Tentukan persamaan-persamaan vector, parametrik dan simetrik untuk garis yang melalui
titik A(3, 2, 2) dan B(5, 6, 4) !
Jawab:
Sebuah vector yang sejajar dengan garis AB adalah
𝑣 = 𝐴𝐵 = 5 − 3, 6 − 2, 4 − 2 = 2, 4, 2
Dipilih

23. Terimakasih!!