DD
Uploaded byDr.rukmani Devi
160 views

gan.pdf

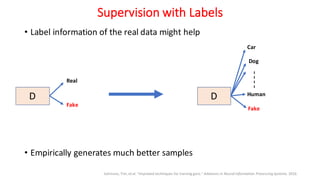
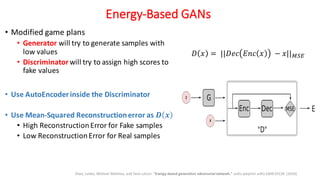
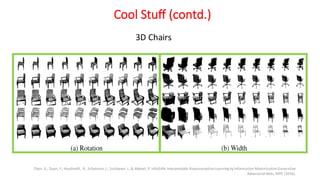
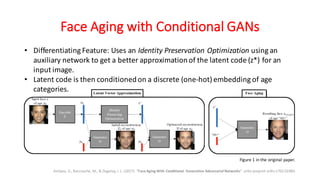
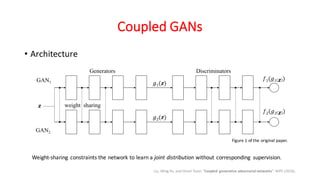
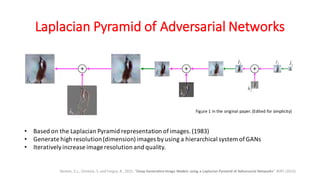
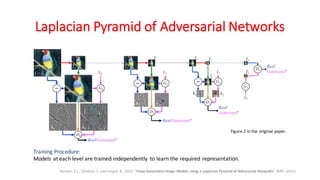
Generative Adversarial Networks (GANs) are a class of deep learning models that are trained using an adversarial process. GANs consist of two neural networks, a generator and a discriminator, that compete against each other. The generator tries to generate new samples from a latent space to fool the discriminator, while the discriminator tries to distinguish real samples from fake ones. GANs can learn complex high-dimensional distributions and have been applied to image generation, video generation, and other domains. However, training GANs is challenging due to issues like non-convergence and mode collapse. Recent work has explored techniques like minibatch discrimination, conditional GANs, and unrolled GANs to help address these training issues.

Embed presentation

Downloaded 11 times
Generative Adversarial Networks (GANs) From Ian Goodfellow et al. A short tutorial by :- Binglin, Shashank & Bhargav
Outline • Part 1: Introduction to GANs • Part 2: Some challenges with GANs • Part 3: Applications of GANs
Part 1 • Motivation for Generative Models • From Adversarial Training to GANs • GAN’s Architecture • GAN’s objective • DCGANs
GANs • Generative • Learn a generative model • Adversarial • Trained in an adversarial setting • Networks • Use Deep Neural Networks
Why Generative Models? • We’ve only seen discriminative models so far • Given an image X, predict a label Y • Estimates P(Y|X) • Discriminative models have several key limitations • Can’t model P(X), i.e. the probabilityof seeing a certain image • Thus, can’t sample from P(X), i.e. can’t generate new images • Generative models (in general) cope with all of above • Can model P(X) • Can generate new images
Magic of GANs… Lotter, William, Gabriel Kreiman, andDavid Cox. "Unsupervised learning of visual structure using predictive generative networks." arXiv preprint arXiv:1511.06380 (2015).
Magic of GANs… Ledig, Christian, et al. "Photo-realistic single image super-resolutionusing a generative adversarial network." arXiv preprint arXiv:1609.04802 (2016). Which one is Computer generated?
Magic of GANs… http://people.eecs.berkeley.edu/~junyanz/projects/gvm/
Adversarial Training • In the last lecture, we saw: • We can generate adversarial samples to fool a discriminativemodel • We can use those adversarial samples to make models robust • We then require more effort to generate adversarial samples • Repeat this and we get betterdiscriminative model • GANs extend that idea to generative models: • Generator: generate fake samples, tries to fool the Discriminator • Discriminator: tries to distinguishbetween real and fake samples • Train them against each other • Repeat this and we get better Generator and Discriminator
GAN’s Architecture • Z is some random noise (Gaussian/Uniform). • Z can be thought as the latent representationof the image. z G(z) D(x) x D(G(z)) G D https://www.slideshare.net/xavigiro/deep-learning-for-computer-vision-generative-models-and-adversarial-training-upc-2016
Training Discriminator https://www.slideshare.net/xavigiro/deep-learning-for-computer-vision-generative-models-and-adversarial-training-upc-2016
Training Generator https://www.slideshare.net/xavigiro/deep-learning-for-computer-vision-generative-models-and-adversarial-training-upc-2016
https://openai.com/blog/generative-models/ Generator in action
GAN’s formulation min $ max ' 𝑉 𝐷, 𝐺 • It is formulated as a minimax game, where: • The Discriminator is trying to maximize its reward 𝑽 𝑫, 𝑮 • The Generator is trying to minimize Discriminator’s reward (or maximize its loss) 𝑉 𝐷, 𝐺 = 𝔼1∼3(1) log𝐷 𝑥 + 𝔼;∼<(;) log 1 − 𝐷 𝐺(𝑧) • The Nash equilibrium of this particular game is achieved at: • 𝑃ABCB 𝑥 = 𝑃 DEF 𝑥 ∀𝑥 • D 𝑥 = I J ∀𝑥
Discriminator updates Generator updates
Vanishing gradient strikes back again… min $ max ' 𝑉 𝐷, 𝐺 𝑉 𝐷, 𝐺 = 𝔼1∼3(1) log𝐷 𝑥 + 𝔼;∼<(;) log 1 − 𝐷 𝐺(𝑧) 𝛻LM 𝑉(𝐷, 𝐺) = 𝛻LM 𝔼;~<(;) log 1 − 𝐷 𝐺 𝑧 • 𝛻B log 1 − 𝜎 𝑎 = QRS T(B) IQ T(B) = QT B IQT B IQ T(B) = −𝜎 𝑎 = −𝐷 𝐺 𝑧 • Gradient goes to 0 if 𝐷 is confident,i.e. 𝐷 𝐺 𝑧 → 0 • Minimize −𝔼;~< ; log𝐷 𝐺 𝑧 for Generator instead (keep Discriminator as it is)
Goodfellow, Ian, et al. "Generative adversarial nets." Advances in neural information processing systems. 2014. Faces
Goodfellow, Ian, et al. "Generative adversarial nets." Advances in neural information processing systems. 2014. CIFAR
DCGAN: Bedroom images Radford, Alec, Luke Metz, and SoumithChintala. "Unsupervised representationlearning withdeep convolutional generative adversarial networks." arXiv:1511.06434 (2015).
Deep Convolutional GANs (DCGANs) Generator Architecture Radford, Alec, Luke Metz, and SoumithChintala. "Unsupervised representationlearning withdeep convolutional generative adversarial networks." arXiv:1511.06434 (2015). Key ideas: • Replace FC hidden layers with Convolutions • Generator:Fractional-Strided convolutions • Use Batch Normalization after each layer • Inside Generator • Use ReLU for hidden layers • Use Tanh for the output layer
Latent vectors capture interesting patterns… Radford, Alec, Luke Metz, and SoumithChintala. "Unsupervised representationlearning withdeep convolutional generative adversarial networks." arXiv:1511.06434 (2015).
Part 2 • Advantages of GANs • Training Challenges • Non-Convergence • Mode-Collapse • Proposed Solutions • Supervision with Labels • Mini-Batch GANs • Modification of GAN’s losses • Discriminator (EB-GAN) • Generator (InfoGAN)
Advantages of GANs • Plenty of existing work on Deep Generative Models • Boltzmann Machine • Deep Belief Nets • Variational AutoEncoders(VAE) • Why GANs? • Sampling (or generation) is straightforward. • Training doesn't involveMaximum Likelihoodestimation. • Robust to Overfitting since Generator never sees the training data. • Empirically, GANs are good at capturing the modes of the distribution. Goodfellow, Ian. "NIPS 2016 Tutorial: Generative Adversarial Networks." arXiv preprint arXiv:1701.00160 (2016).
Problems with GANs • Probability Distribution is Implicit • Not straightforward to compute P(X). • Thus Vanilla GANs are only good for Sampling/Generation. • Training is Hard • Non-Convergence • Mode-Collapse Goodfellow, Ian. "NIPS 2016 Tutorial: Generative Adversarial Networks." arXiv preprint arXiv:1701.00160 (2016).
Training Problems •Non-Convergence •Mode-Collapse
min $ max ' 𝑉 𝐷, 𝐺 • Deep Learning models (in general) involve a single player • The player tries to maximizeits reward (minimizeits loss). • Use SGD (with Backpropagation) to find the optimal parameters. • SGD has convergenceguarantees (under certain conditions). • Problem: With non-convexity,we might convergeto local optima. min $ 𝐿 𝐺 • GANs instead involve two (or more) players • Discriminator is trying to maximizeits reward. • Generator is trying to minimizeDiscriminator’sreward. • SGD was not designed to find the Nash equilibrium of a game. • Problem: We might not converge to the Nash equilibrium at all. Salimans, Tim, et al. "Improved techniques for training gans." Advances in Neural Information Processing Systems. 2016.
Non-Convergence min 1 max X 𝑉 𝑥, 𝑦 Let 𝑉 𝑥, 𝑦 = 𝑥𝑦 • State 1: • State 2: • State 3: • State 4 : • State 5: == State 1 x > 0 y > 0 V > 0 Increase y Decrease x Decrease y Decrease x Decrease y Increase x Increase y Increase x Increase y Decrease x x < 0 y > 0 V < 0 x < 0 y < 0 V > 0 x > 0 y < 0 V < 0 x > 0 y > 0 V > 0
Non-Convergence min 1 max X 𝑥𝑦 • Z Z1 = −y … Z ZX = x • Z] ZX] = Z Z1 = −𝑦 • Differential equation’ssolutionhas sinusoidal terms • Even with a small learning rate, it will not converge Goodfellow, Ian. "NIPS 2016 Tutorial: Generative Adversarial Networks." arXiv preprint arXiv:1701.00160 (2016).
Problems with GANs •Non-Convergence •Mode-Collapse
Mode-Collapse • Generator fails to output diverse samples Metz, Luke, et al. "Unrolled Generative Adversarial Networks." arXiv preprint arXiv:1611.02163 (2016). Expected Output Target
Some real examples Reed, S., et al. Generating interpretable images with controllable structure. Technical report, 2016. 2, 2016.
Some Solutions • Mini-Batch GANs • Supervision with labels • Some recent attempts :- • Unrolled GANs • W-GANs
Basic (Heuristic) Solutions • Mini-Batch GANs • Supervision with labels
How to reward sample diversity? • At Mode Collapse, • Generator produces good samples, but a very few of them. • Thus, Discriminator can’t tag them as fake. • To address this problem, • Let the Discriminator know about this edge-case. • More formally, • Let the Discriminator look at the entire batch instead of single examples • If there is lack of diversity, it will mark the examples as fake • Thus, • Generator will be forced to produce diverse samples. Salimans, Tim, et al. "Improved techniques for training gans." Advances in Neural Information Processing Systems. 2016.
Mini-Batch GANs • Extract features that capture diversity in the mini-batch • For e.g. L2 norm of the difference between all pairs from the batch • Feed those features to the discriminator along with the image • Feature values will differ b/w diverse and non-diverse batches • Thus, Discriminator will rely on those features for classification • This in turn, • Will force the Generator to match those feature values with the real data • Will generate diverse batches Salimans, Tim, et al. "Improved techniques for training gans." Advances in Neural Information Processing Systems. 2016.
Basic (Heuristic) Solutions • Mini-Batch GANs • Supervision with labels
Supervision with Labels • Label information of the real data might help • Empirically generates much better samples Salimans, Tim, et al. "Improved techniques for training gans." Advances in Neural Information Processing Systems. 2016. D Real Fake D Human Fake Car Dog
Alternate view of GANs min $ max ' 𝑉 𝐷,𝐺 𝑉 𝐷, 𝐺 = 𝔼1∼3(1) log 𝐷 𝑥 + 𝔼;∼<(;) log 1 − 𝐷 𝐺(𝑧) 𝐷∗ = 𝑎𝑟𝑔max ' 𝑉 𝐷, 𝐺 𝐺∗ = 𝑎𝑟𝑔m𝑖𝑛 $ 𝑉 𝐷, 𝐺 • In this formulation,Discriminator’s strategy was 𝐷 𝑥 → 1, 𝐷 𝐺 𝑧 → 0 • Alternatively, we can flip the binary classification labels i.e. Fake = 1, Real = 0 𝑉 𝐷,𝐺 = 𝔼1∼3(1) log 1 − 𝐷 𝑥 + 𝔼;∼<(;) log 𝐷 𝐺(𝑧) • In this new formulation,Discriminator’s strategy will be 𝐷 𝑥 → 0, 𝐷 𝐺 𝑧 → 1 Zhao, Junbo, Michael Mathieu, and Yann LeCun. "Energy-based generative adversarial network." arXiv preprint arXiv:1609.03126 (2016)
Alternate view of GANs (Contd.) • If all we want to encode is 𝐷 𝑥 → 0, 𝐷 𝐺 𝑧 → 1 𝐷∗ = 𝑎𝑟𝑔𝑚𝑎𝑥' 𝔼1∼3(1) log 1 − 𝐷 𝑥 + 𝔼;∼<(;) log 𝐷 𝐺(𝑧) 𝐷∗ = 𝑎𝑟𝑔𝑚𝑖𝑛' 𝔼1∼3 1 log 𝐷 𝑥 + 𝔼;∼<(;) log 1 − 𝐷 𝐺 𝑧 • Now, we can replace cross-entropy with any loss function (Hinge Loss) 𝐷∗ = 𝑎𝑟𝑔𝑚𝑖𝑛' 𝔼1∼3 1 𝐷 𝑥 + 𝔼;∼< ; max 0, 𝑚 − 𝐷 𝐺 𝑧 • And thus, instead of outputtingprobabilities,Discriminator just has to output:- • High values for fake samples • Low values for real samples Zhao, Junbo, Michael Mathieu, and Yann LeCun. "Energy-based generative adversarial network." arXiv preprint arXiv:1609.03126 (2016) We can use this
Energy-Based GANs • Modified game plans • Generator will try to generate samples with low values • Discriminatorwill try to assign high scores to fake values • Use AutoEncoderinside the Discriminator • Use Mean-Squared Reconstructionerror as 𝑫 𝒙 • High ReconstructionError for Fake samples • Low ReconstructionError for Real samples Zhao, Junbo, Michael Mathieu, and Yann LeCun. "Energy-based generative adversarial network." arXiv preprint arXiv:1609.03126 (2016) 𝐷 𝑥 = ||𝐷𝑒𝑐 𝐸𝑛𝑐 𝑥 − 𝑥||ijk
More Bedrooms… Zhao, Junbo, Michael Mathieu, and Yann LeCun. "Energy-based generative adversarial network." arXiv preprint arXiv:1609.03126 (2016)
Celebs…
The Cool Stuff… 3D Faces Chen, X., Duan, Y., Houthooft, R., Schulman, J., Sutskever, I., & Abbeel, P. InfoGAN:Interpretable RepresentationLearning by Information MaximizationGenerative Adversarial Nets, NIPS (2016).
Chen, X., Duan, Y., Houthooft, R., Schulman, J., Sutskever, I., & Abbeel, P. InfoGAN:Interpretable RepresentationLearning by Information MaximizationGenerative Adversarial Nets, NIPS (2016). 3D Chairs Cool Stuff (contd.)
How to reward Disentanglement? Chen, X., Duan, Y., Houthooft, R., Schulman, J., Sutskever, I., & Abbeel, P. InfoGAN:Interpretable RepresentationLearning by Information MaximizationGenerative Adversarial Nets • Disentanglement means individual dimensions independently capturing key attributes of the image • Let’s partition the noise vector into 2 parts :- • z vector will capture slight variations in the image • c vector will capture the main attributes of the image • For e.g. Digit, Angle and Thickness of images in MNIST • If c vector captures the key variations in the image, Will c and 𝒙𝒇𝒂𝒌𝒆 be highly correlated or weakly correlated?
Recap: Mutual Information • Mutual Information captures the mutual dependence between two variables • Mutual informationbetween two variables 𝑿,𝒀 is defined as: 𝐼 𝑋; 𝑌 = v 𝑝 𝑥, 𝑦 log 𝑝 𝑥, 𝑦 𝑝 𝑥 𝑝 𝑦 1,X 𝐼 𝑋; 𝑌 = 𝐻 𝑋 − 𝐻 𝑋 𝑌 = H Y − H(Y|X)
InfoGAN • We want to maximize the mutual information 𝐼 between 𝒄 and 𝐱 = 𝑮(𝒛, 𝒄) • Incorporate in the value function of the minimax game. Chen, X., Duan, Y., Houthooft, R., Schulman, J., Sutskever, I., & Abbeel, P. InfoGAN:Interpretable RepresentationLearning by Information MaximizationGenerative Adversarial Nets, NIPS (2016). min $ max ' 𝑉• 𝐷, 𝐺 = 𝑉 𝐷, 𝐺 − 𝜆 𝐼 𝑐; 𝐺 𝑧, 𝑐
Mutual Information’s Variational Lower bound 𝐼 𝑐; 𝐺 𝑧, 𝑐 = 𝐻 𝑐 − 𝐻 𝑐 𝐺 𝑧, 𝑐 = 𝔼1 ~ $ ;,• 𝔼•‚ ~ ƒ 𝑐 𝑥 log𝑃 𝑐„ 𝑥 + 𝐻(𝑐) = 𝔼1 ~ $ ;,• 𝐷…†(𝑃| 𝑄 + 𝔼•‚ ~ ƒ 𝑐 𝑥 log𝑄 𝑐„ 𝑥 + 𝐻(𝑐) ≥ 𝔼1 ~ $ ;,• 𝔼•‚ ~ ƒ 𝑐 𝑥 log𝑄 𝑐„ 𝑥 + 𝐻(𝑐) ≥ 𝔼•~ƒ • , 1 ~ $ ;,• 𝐥𝐨𝐠 𝑸(𝒄|𝒙) + 𝐻(𝑐) Chen, X., Duan, Y., Houthooft, R., Schulman, J., Sutskever, I., & Abbeel, P. InfoGAN:Interpretable RepresentationLearning by Information MaximizationGenerative Adversarial Nets, NIPS (2016). InfoGAN 𝐷 𝑄
Part 3 • Conditional GANs • Applications • Image-to-Image Translation • Text-to-Image Synthesis • Face Aging • Advanced GAN Extensions • Coupled GAN • LAPGAN – Laplacian Pyramid of Adversarial Networks • Adversarially Learned Inference • Summary
Conditional GANs Mirza, Mehdi, and Simon Osindero. Conditional generative adversarial nets. arXiv preprint arXiv:1411.1784 (2014). Figure 2 in the original paper. generated conditioned on their class label. 1, 0, 0,0, 0, 0, 0, 0, 0, 0 0, 1, 0,0, 0, 0, 0, 0, 0, 0 0, 0, 1,0, 0, 0, 0, 0, 0, 0 0, 0, 0,1, 0, 0, 0, 0, 0, 0 0, 0, 0,0, 1, 0, 0, 0, 0, 0 0, 0, 0,0, 0, 1, 0, 0, 0, 0 0, 0, 0,0, 0, 0, 1, 0, 0, 0 0, 0, 0,0, 0, 0, 0, 1, 0, 0 0, 0, 0,0, 0, 0, 0, 0, 1, 0 0, 0, 0,0, 0, 0, 0, 0, 0, 1 MNIST digits MNIST digits
Conditional GANs • Simple modification to the original GAN framework that conditions the model on additional information for better multi-modal learning. • Lends to many practical applications of GANs when we have explicit supervision available. Mirza, Mehdi, and Simon Osindero. “Conditional generative adversarial nets”. arXiv preprint arXiv:1411.1784 (2014). Image Credit: Figure 2 inOdena, A., Olah, C. and Shlens, J., 2016. Conditional image synthesis withauxiliaryclassifier GANs. arXiv preprint arXiv:1610.09585.
Part 3 • Conditional GANs • Applications • Image-to-Image Translation • Text-to-Image Synthesis • Face Aging • Advanced GAN Extensions • Coupled GAN • LAPGAN – Laplacian Pyramid of Adversarial Networks • Adversarially Learned Inference • Summary
Image-to-Image Translation Isola, P., Zhu, J. Y., Zhou, T., & Efros, A. A. “Image-to-image translation with conditional adversarial networks”. arXiv preprint arXiv:1611.07004. (2016). Figure 1 in the original paper. Link to an interactive demo of this paper
Image-to-Image Translation • Architecture: DCGAN-based architecture • Training is conditioned on the images from the source domain. • Conditional GANs provide an effective way to handle many complex domains without worrying about designing structured loss functions explicitly. Isola, P., Zhu, J. Y., Zhou, T., & Efros, A. A. “Image-to-image translation with conditional adversarial networks”. arXiv preprint arXiv:1611.07004. (2016). Figure 2 in the original paper.
Text-to-Image Synthesis Reed, S., Akata, Z., Yan, X., Logeswaran, L., Schiele, B., & Lee, H. “Generative adversarial text to image synthesis”. ICML (2016). Figure 1 in the original paper. Motivation Given a text description, generate images closely associated. Uses a conditional GAN with the generator and discriminator being condition on “dense” text embedding.
Text-to-Image Synthesis Reed, S., Akata, Z., Yan, X., Logeswaran, L., Schiele, B., & Lee, H. “Generative adversarial text to image synthesis”. ICML (2016). Figure 2 in the original paper. Positive Example: Real Image, Right Text Negative Examples: Real Image, Wrong Text Fake Image, Right Text
Face Aging with Conditional GANs Antipov, G., Baccouche, M., & Dugelay, J. L. (2017). “Face Aging With Conditional Generative Adversarial Networks”. arXiv preprint arXiv:1702.01983. Figure 1 in the original paper. • Differentiating Feature: Uses an Identity Preservation Optimization using an auxiliary network to get a better approximationof the latent code (z*) for an input image. • Latent code is then conditionedon a discrete (one-hot) embedding of age categories.
Face Aging with Conditional GANs Antipov, G., Baccouche, M., & Dugelay, J. L. (2017). “Face Aging With Conditional Generative Adversarial Networks”. arXiv preprint arXiv:1702.01983. Figure 3 in the original paper.
Conditional GANs Conditional Model Collapse • Scenario observed when the ConditionalGAN starts ignoring either the code (c) or the noise variables (z). • This limits the diversity of images generated. Mirza, Mehdi, and Simon Osindero. Conditional generative adversarial nets. arXiv preprint arXiv:1411.1784 (2014). Credit?
Part 3 • Conditional GANs • Applications • Image-to-Image Translation • Text-to-Image Synthesis • Face Aging • Advanced GAN Extensions • Coupled GAN • LAPGAN – Laplacian Pyramid of Adversarial Networks • Adversarially Learned Inference • Summary
Coupled GAN • Learning a joint distribution of multi-domain images. • Using GANs to learn the joint distribution with samples drawn from the marginal distributions. • Direct applications in domain adaptation and image translation. Liu, Ming-Yu, and Oncel Tuzel. “Coupled generative adversarial networks”. NIPS (2016). Figure 2 in the original paper.
Coupled GANs • Architecture Liu, Ming-Yu, and Oncel Tuzel. “Coupled generative adversarial networks”. NIPS (2016). Weight-sharing constraints the network to learn a joint distribution without corresponding supervision. Figure 1 of the original paper.
Coupled GANs Liu, Ming-Yu, and Oncel Tuzel. “Coupled generative adversarial networks”. NIPS (2016). • Some examples of generating facial images across different feature domains. • Correspondingimages in a column are generate from the same latent code 𝑧 Figure 4 in the original paper. Hair Color Facial Expression Sunglasses
Laplacian Pyramid of Adversarial Networks Denton, E.L., Chintala, S. and Fergus, R., 2015. “Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks”. NIPS (2015) Figure 1 in the original paper. (Edited for simplicity) • Based on the Laplacian Pyramid representation ofimages.(1983) • Generate high resolution(dimension)images byusing a hierarchical system ofGANs • Iterativelyincrease image resolution and quality.
Laplacian Pyramid of Adversarial Networks Denton, E.L., Chintala, S. and Fergus, R., 2015. “Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks”. NIPS (2015) Figure 1 in the original paper. Image Generation using a LAPGAN • Generator 𝐺• generatesthe base image 𝐼• Ž from random noise input 𝑧•. • Generators (𝐺J,𝐺I,𝐺•)iterativelygenerate the difference image (ℎ ‘) conditionedon previous small image (𝑙). • This difference image is added to an up-scaled version of previous smaller image.
Laplacian Pyramid of Adversarial Networks Denton, E.L., Chintala, S. and Fergus, R., 2015. “Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks”. NIPS (2015) Figure 2 in the original paper. Training Procedure: Models at each level are trained independently to learn the required representation.
Adversarially Learned Inference • Basic idea is to learn an encoder/inferencenetwork along with the generator network. • Consider the following joint distributions over 𝑥 (image) and 𝑧 (latent variables) : 𝑞 𝑥, 𝑧 = 𝑞 𝑥 𝑞(𝑧|𝑥) 𝑝 𝑥, 𝑧 = 𝑝 𝑧 𝑝(𝑥|𝑧) Dumoulin, Vincent, et al. “Adversarially learned inference”. arXiv preprint arXiv:1606.00704 (2016). encoder distribution generator distribution
Adversarially Learned Inference Dumoulin, Vincent, et al. “Adversarially learned inference”. arXiv preprint arXiv:1606.00704 (2016). min $ max ' 𝔼< 1 [log 𝐷 𝑥, 𝐺; 𝑥 + 𝔼3 1 log 1 − 𝐷 𝐺1 𝑧 , 𝑧 Generator Network Encoder/Inference Network Discriminator Network Figure 1 in the original paper.
Adversarially Learned Inference • Nash equilibrium yields • Joint: 𝑝 𝑥, 𝑧 ~ 𝑞 𝑥, 𝑧 • Marginals: 𝑝 𝑥 ~ 𝑞 𝑥 and 𝑝 𝑧 ~ 𝑞 𝑧 • Conditionals: 𝑝 𝑥|𝑧 ~ 𝑞(𝑥|𝑧) and 𝑝 𝑧|𝑥 ~ 𝑞 𝑧|𝑥 • Inferred latent representation successfully reconstructed the original image. • Representation was useful in the downstream semi-supervised task. Dumoulin, Vincent, et al. “Adversarially learned inference”. arXiv preprint arXiv:1606.00704 (2016).
Summary • GANs are generative models that are implemented using two stochastic neural network modules: Generator and Discriminator. • Generator tries to generate samples from random noise as input • Discriminatortries to distinguish the samples from Generator and samples from the real data distribution. • Both networksare trained adversarially (in tandem) to fool the other component. In this process, both models become better at their respective tasks.
Why use GANs for Generation? • Can be trained using back-propagation for Neural Network based Generator/Discriminator functions. • Sharper images can be generated. • Faster to sample from the model distribution: single forward pass generates a single sample.
Reading List • Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair,S., Courville, A.and Bengio, Y. Generative adversarial nets, NIPS (2014). • Goodfellow, Ian NIPS 2016 Tutorial: Generative Adversarial Networks, NIPS (2016). • Radford,A., Metz, L. and Chintala, S., Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv preprint arXiv:1511.06434.(2015). • Salimans, T., Goodfellow, I., Zaremba, W.,Cheung, V., Radford,A., & Chen, X. Improved techniques for training gans. NIPS (2016). • Chen, X., Duan, Y., Houthooft, R., Schulman, J., Sutskever, I., & Abbeel, P. InfoGAN: Interpretable Representation Learning by Information Maximization Generative Adversarial Nets, NIPS (2016). • Zhao, Junbo, Michael Mathieu, and Yann LeCun. Energy-based generative adversarial network. arXiv preprint arXiv:1609.03126(2016). • Mirza, Mehdi, and Simon Osindero.Conditional generative adversarial nets. arXiv preprintarXiv:1411.1784 (2014). • Liu, Ming-Yu, and Oncel Tuzel. Coupled generative adversarial networks. NIPS (2016). • Denton, E.L., Chintala, S. and Fergus, R., 2015.Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks. NIPS (2015) • Dumoulin, V., Belghazi, I., Poole, B., Lamb, A., Arjovsky,M., Mastropietro, O., & Courville, A. Adversarially learned inference. arXiv preprint arXiv:1606.00704 (2016). Applications: • Isola, P., Zhu, J. Y., Zhou, T., & Efros,A. A. Image-to-image translation with conditional adversarial networks. arXiv preprintarXiv:1611.07004.(2016). • Reed, S., Akata, Z., Yan, X., Logeswaran, L., Schiele, B., & Lee, H. Generative adversarial text to image synthesis. JMLR (2016). • Antipov,G., Baccouche, M., & Dugelay, J. L. (2017).Face Aging With Conditional Generative Adversarial Networks. arXiv preprintarXiv:1702.01983.
Questions?

More Related Content

PPTX
Generative Adversarial Networks (GAN)
byManohar Mukku
 
PDF
Introduction to Diffusion Models
bySangwoo Mo
 
PDF
Introduction to Generative Adversarial Networks (GANs)
byAppsilon Data Science
 
PPTX
A (Very) Gentle Introduction to Generative Adversarial Networks (a.k.a GANs)
byThomas da Silva Paula
 
PPTX
Diffusion models beat gans on image synthesis
byBeerenSahu
 
PDF
Generative adversarial networks
byYunjey Choi
 
PDF
GANs and Applications
byHoang Nguyen
 
PPTX
GANs Presentation.pptx
byMAHMOUD729246
 
Generative Adversarial Networks (GAN)
byManohar Mukku
 
Introduction to Diffusion Models
bySangwoo Mo
 
Introduction to Generative Adversarial Networks (GANs)
byAppsilon Data Science
 
A (Very) Gentle Introduction to Generative Adversarial Networks (a.k.a GANs)
byThomas da Silva Paula
 
Diffusion models beat gans on image synthesis
byBeerenSahu
 
Generative adversarial networks
byYunjey Choi
 
GANs and Applications
byHoang Nguyen
 
GANs Presentation.pptx
byMAHMOUD729246
 

What's hot

PDF
Introduction To Generative Adversarial Networks GANs
byHichem Felouat
 
PPTX
Generative Adversarial Network (GAN)
byPrakhar Rastogi
 
PPTX
Recurrent neural network
bySyed Annus Ali SHah
 
PPTX
Generative Adversarial Network (GANs).
bykgandham169
 
PPTX
Generative Adversarial Networks (GANs)
byAmol Patil
 
PDF
Generative adversarial networks
by남주 김
 
PDF
Recurrent Neural Networks, LSTM and GRU
byananth
 
PDF
Transformers in 2021
byGrigory Sapunov
 
PDF
Introduction to Recurrent Neural Network
byYan Xu
 
PDF
Generative Adversarial Networks
byMustafa Yagmur
 
PPTX
Dimensionality Reduction | Machine Learning | CloudxLab
byCloudxLab
 
PDF
Variational Autoencoders VAE - Santiago Pascual - UPC Barcelona 2018
byUniversitat Politècnica de Catalunya
 
PDF
Evolution of the StyleGAN family
byVitaly Bondar
 
PPTX
Generative Adversarial Network (GAN) for Image Synthesis
byRiwaz Mahat
 
PPTX
Transfer Learning and Fine-tuning Deep Neural Networks
byPyData
 
PPTX
Normalization 방법
by홍배 김
 
PDF
Convolutional neural network
byYan Xu
 
PDF
A brief overview of Reinforcement Learning applied to games
byThomas da Silva Paula
 
PDF
Understanding cnn
byRucha Gole
 
PDF
Basic Generative Adversarial Networks
byDong Heon Cho
 
Introduction To Generative Adversarial Networks GANs
byHichem Felouat
 
Generative Adversarial Network (GAN)
byPrakhar Rastogi
 
Recurrent neural network
bySyed Annus Ali SHah
 
Generative Adversarial Network (GANs).
bykgandham169
 
Generative Adversarial Networks (GANs)
byAmol Patil
 
Generative adversarial networks
by남주 김
 
Recurrent Neural Networks, LSTM and GRU
byananth
 
Transformers in 2021
byGrigory Sapunov
 
Introduction to Recurrent Neural Network
byYan Xu
 
Generative Adversarial Networks
byMustafa Yagmur
 
Dimensionality Reduction | Machine Learning | CloudxLab
byCloudxLab
 
Variational Autoencoders VAE - Santiago Pascual - UPC Barcelona 2018
byUniversitat Politècnica de Catalunya
 
Evolution of the StyleGAN family
byVitaly Bondar
 
Generative Adversarial Network (GAN) for Image Synthesis
byRiwaz Mahat
 
Transfer Learning and Fine-tuning Deep Neural Networks
byPyData
 
Normalization 방법
by홍배 김
 
Convolutional neural network
byYan Xu
 
A brief overview of Reinforcement Learning applied to games
byThomas da Silva Paula
 
Understanding cnn
byRucha Gole
 
Basic Generative Adversarial Networks
byDong Heon Cho
 

Similar to gan.pdf

PPTX
GAN_SANTHOSH KUMAR_Architecture_in_network
bySanthoshKumar229321
 
PPTX
gan-190318135433 (1).pptx
bykiran814572
 
PPTX
Seminar PPT for quantam computing explaining about the mechanism of quantam c...
byeeleetsuperbrialch
 
PPT
GNA 13552928 deep learning for GAN a.ppt
byManiMaran230751
 
PDF
Deep Generative Models II (DLAI D10L1 2017 UPC Deep Learning for Artificial I...
byUniversitat Politècnica de Catalunya
 
PPTX
GAN Deep Learning Approaches to Image Processing Applications (1).pptx
byRMDAcademicCoordinat
 
PDF
Unsupervised learning represenation with DCGAN
byShyam Krishna Khadka
 
PPTX
GAN Deep. Learning architecture and applications.pptx
byb74104635
 
PDF
gans_copy.pdfhjsjsisidkskskkskwkduydjekedj
byfahid32446
 
PDF
Introduction to Generative Adversarial Network
byvaidehimadaan041
 
PDF
Generative Adversarial Networks GAN - Xavier Giro - UPC TelecomBCN Barcelona ...
byUniversitat Politècnica de Catalunya
 
PDF
11_gan.pdf
byAnkush84837
 
PDF
GAN.pdf
byNiharikaThakur32
 
PDF
M4L19 Generative Models - Slides v 3.pdf
byyireme8491
 
PDF
Jakub Langr (University of Oxford) - Overview of Generative Adversarial Netwo...
byCodiax
 
PDF
1시간만에 GAN(Generative Adversarial Network) 완전 정복하기
byNAVER Engineering
 
PPTX
Module4_GAN.pptxgdgdijehejejjejejejhehjdd
byHrushikeshDandu
 
PPTX
GAN.pptx
byHemanthKonamanchili1
 
PDF
Exploring Generative AI with GAN Models
byKonfHubTechConferenc
 
PPTX
Generative Adversarial Networks inn Deep learning
bydrrajeshkannablr
 
GAN_SANTHOSH KUMAR_Architecture_in_network
bySanthoshKumar229321
 
gan-190318135433 (1).pptx
bykiran814572
 
Seminar PPT for quantam computing explaining about the mechanism of quantam c...
byeeleetsuperbrialch
 
GNA 13552928 deep learning for GAN a.ppt
byManiMaran230751
 
Deep Generative Models II (DLAI D10L1 2017 UPC Deep Learning for Artificial I...
byUniversitat Politècnica de Catalunya
 
GAN Deep Learning Approaches to Image Processing Applications (1).pptx
byRMDAcademicCoordinat
 
Unsupervised learning represenation with DCGAN
byShyam Krishna Khadka
 
GAN Deep. Learning architecture and applications.pptx
byb74104635
 
gans_copy.pdfhjsjsisidkskskkskwkduydjekedj
byfahid32446
 
Introduction to Generative Adversarial Network
byvaidehimadaan041
 
Generative Adversarial Networks GAN - Xavier Giro - UPC TelecomBCN Barcelona ...
byUniversitat Politècnica de Catalunya
 
11_gan.pdf
byAnkush84837
 
GAN.pdf
byNiharikaThakur32
 
M4L19 Generative Models - Slides v 3.pdf
byyireme8491
 
Jakub Langr (University of Oxford) - Overview of Generative Adversarial Netwo...
byCodiax
 
1시간만에 GAN(Generative Adversarial Network) 완전 정복하기
byNAVER Engineering
 
Module4_GAN.pptxgdgdijehejejjejejejhehjdd
byHrushikeshDandu
 
GAN.pptx
byHemanthKonamanchili1
 
Exploring Generative AI with GAN Models
byKonfHubTechConferenc
 
Generative Adversarial Networks inn Deep learning
bydrrajeshkannablr
 

Recently uploaded

PPTX
RTOS_Automatic_Room_Light_Controller_ Exp.no.1.pptx
bySanjivani College of Engineering, Kopargaon, Ahmednagar, Maharashtra, India
 
PDF
Life Cycle Analysis of Electric and Internal Combustion Engine Vehicles
byUniversity Institute of Technology, Barkatullah University
 
PDF
Foundations of AI and ML - Mechanical Engineering Perspectives.pdf
byVyankateshBhaurkar1
 
PDF
SURAJIT PARAMANIK_ME_3RD_THERMODYNAMICS.pdf
byastikparamanik1970
 
PPTX
MET 464- MICRO AND AND NANO MANUFACTURING -MOD 2.pptx KTU 2019
byVINAY B
 
PDF
The Eternal Citadel Architecture, Sacred Geography, and the Resilience of Som...
byAman Kumar Singh
 
PPTX
Why Precision Matters CO2 N2 Gas Filling Systems Neometrix
byNeometrix_Engineering_Pvt_Ltd
 
PDF
graph graph graph theory Graph presentation .pdf
bygeekcooder2020
 
PDF
Digital_Signal_Processing_for_FIR_filterspdf
bytunacevik03
 
PPTX
review of transistor circuit and applications
bysophieshuqinghuang
 
PPTX
PEMET 413 KTU 2024 SCHEME MODULE 2 LECTURE 4.pptx
byVINAY B
 
PPTX
High Voltage Direct Current Circuit Breakers.pptx
byJawadAmjad16
 
PPTX
Embedded_Linux_ARM_Cross_Compilation_Exp.no.3.pptx
bySanjivani College of Engineering, Kopargaon, Ahmednagar, Maharashtra, India
 
PDF
Java Programming core java and basics concepts
byHarish Khodke
 
PPTX
The Most Dangerous Asset in Your Plant Is the One You Ignore | CXO Guide to H...
byMaintWiz Technologies Private Limited
 
PDF
UNIT02_TRE_GEOMETRIC DESIGN.pdf_________
byAaquib Ansari
 
PPTX
70,000 RPM Aerospace Bearing Testing – Why High-Speed Validation Is Critical
byNeometrix_Engineering_Pvt_Ltd
 
PPTX
Power Electronics_PE_lecture_10_presentation .pptx
bykavitabani2
 
PDF
TU/e - 2025-2026 - Lecture Geotechnics 3 - Arkesteijn
byRuud Arkesteijn
 
PDF
Performance_Metrics_Evolution_DannyJiang
byDanny Jiang
 
RTOS_Automatic_Room_Light_Controller_ Exp.no.1.pptx
bySanjivani College of Engineering, Kopargaon, Ahmednagar, Maharashtra, India
 
Life Cycle Analysis of Electric and Internal Combustion Engine Vehicles
byUniversity Institute of Technology, Barkatullah University
 
Foundations of AI and ML - Mechanical Engineering Perspectives.pdf
byVyankateshBhaurkar1
 
SURAJIT PARAMANIK_ME_3RD_THERMODYNAMICS.pdf
byastikparamanik1970
 
MET 464- MICRO AND AND NANO MANUFACTURING -MOD 2.pptx KTU 2019
byVINAY B
 
The Eternal Citadel Architecture, Sacred Geography, and the Resilience of Som...
byAman Kumar Singh
 
Why Precision Matters CO2 N2 Gas Filling Systems Neometrix
byNeometrix_Engineering_Pvt_Ltd
 
graph graph graph theory Graph presentation .pdf
bygeekcooder2020
 
Digital_Signal_Processing_for_FIR_filterspdf
bytunacevik03
 
review of transistor circuit and applications
bysophieshuqinghuang
 
PEMET 413 KTU 2024 SCHEME MODULE 2 LECTURE 4.pptx
byVINAY B
 
High Voltage Direct Current Circuit Breakers.pptx
byJawadAmjad16
 
Embedded_Linux_ARM_Cross_Compilation_Exp.no.3.pptx
bySanjivani College of Engineering, Kopargaon, Ahmednagar, Maharashtra, India
 
Java Programming core java and basics concepts
byHarish Khodke
 
The Most Dangerous Asset in Your Plant Is the One You Ignore | CXO Guide to H...
byMaintWiz Technologies Private Limited
 
UNIT02_TRE_GEOMETRIC DESIGN.pdf_________
byAaquib Ansari
 
70,000 RPM Aerospace Bearing Testing – Why High-Speed Validation Is Critical
byNeometrix_Engineering_Pvt_Ltd
 
Power Electronics_PE_lecture_10_presentation .pptx
bykavitabani2
 
TU/e - 2025-2026 - Lecture Geotechnics 3 - Arkesteijn
byRuud Arkesteijn
 
Performance_Metrics_Evolution_DannyJiang
byDanny Jiang
 

gan.pdf

  • 1.
    Generative Adversarial Networks (GANs) FromIan Goodfellow et al. A short tutorial by :- Binglin, Shashank & Bhargav
  • 2.
    Outline • Part 1:Introduction to GANs • Part 2: Some challenges with GANs • Part 3: Applications of GANs
  • 3.
    Part 1 • Motivationfor Generative Models • From Adversarial Training to GANs • GAN’s Architecture • GAN’s objective • DCGANs
  • 4.
    GANs • Generative • Learna generative model • Adversarial • Trained in an adversarial setting • Networks • Use Deep Neural Networks
  • 5.
    Why Generative Models? •We’ve only seen discriminative models so far • Given an image X, predict a label Y • Estimates P(Y|X) • Discriminative models have several key limitations • Can’t model P(X), i.e. the probabilityof seeing a certain image • Thus, can’t sample from P(X), i.e. can’t generate new images • Generative models (in general) cope with all of above • Can model P(X) • Can generate new images
  • 6.
    Magic of GANs… Lotter,William, Gabriel Kreiman, andDavid Cox. "Unsupervised learning of visual structure using predictive generative networks." arXiv preprint arXiv:1511.06380 (2015).
  • 7.
    Magic of GANs… Ledig,Christian, et al. "Photo-realistic single image super-resolutionusing a generative adversarial network." arXiv preprint arXiv:1609.04802 (2016). Which one is Computer generated?
  • 8.
  • 9.
    Adversarial Training • Inthe last lecture, we saw: • We can generate adversarial samples to fool a discriminativemodel • We can use those adversarial samples to make models robust • We then require more effort to generate adversarial samples • Repeat this and we get betterdiscriminative model • GANs extend that idea to generative models: • Generator: generate fake samples, tries to fool the Discriminator • Discriminator: tries to distinguishbetween real and fake samples • Train them against each other • Repeat this and we get better Generator and Discriminator
  • 10.
    GAN’s Architecture • Zis some random noise (Gaussian/Uniform). • Z can be thought as the latent representationof the image. z G(z) D(x) x D(G(z)) G D https://www.slideshare.net/xavigiro/deep-learning-for-computer-vision-generative-models-and-adversarial-training-upc-2016
  • 11.
  • 12.
  • 13.
  • 14.
    GAN’s formulation min $ max ' 𝑉 𝐷,𝐺 • It is formulated as a minimax game, where: • The Discriminator is trying to maximize its reward 𝑽 𝑫, 𝑮 • The Generator is trying to minimize Discriminator’s reward (or maximize its loss) 𝑉 𝐷, 𝐺 = 𝔼1∼3(1) log𝐷 𝑥 + 𝔼;∼<(;) log 1 − 𝐷 𝐺(𝑧) • The Nash equilibrium of this particular game is achieved at: • 𝑃ABCB 𝑥 = 𝑃 DEF 𝑥 ∀𝑥 • D 𝑥 = I J ∀𝑥
  • 15.
  • 16.
    Vanishing gradient strikesback again… min $ max ' 𝑉 𝐷, 𝐺 𝑉 𝐷, 𝐺 = 𝔼1∼3(1) log𝐷 𝑥 + 𝔼;∼<(;) log 1 − 𝐷 𝐺(𝑧) 𝛻LM 𝑉(𝐷, 𝐺) = 𝛻LM 𝔼;~<(;) log 1 − 𝐷 𝐺 𝑧 • 𝛻B log 1 − 𝜎 𝑎 = QRS T(B) IQ T(B) = QT B IQT B IQ T(B) = −𝜎 𝑎 = −𝐷 𝐺 𝑧 • Gradient goes to 0 if 𝐷 is confident,i.e. 𝐷 𝐺 𝑧 → 0 • Minimize −𝔼;~< ; log𝐷 𝐺 𝑧 for Generator instead (keep Discriminator as it is)
  • 17.
    Goodfellow, Ian, etal. "Generative adversarial nets." Advances in neural information processing systems. 2014. Faces
  • 18.
    Goodfellow, Ian, etal. "Generative adversarial nets." Advances in neural information processing systems. 2014. CIFAR
  • 19.
    DCGAN: Bedroom images Radford,Alec, Luke Metz, and SoumithChintala. "Unsupervised representationlearning withdeep convolutional generative adversarial networks." arXiv:1511.06434 (2015).
  • 20.
    Deep Convolutional GANs(DCGANs) Generator Architecture Radford, Alec, Luke Metz, and SoumithChintala. "Unsupervised representationlearning withdeep convolutional generative adversarial networks." arXiv:1511.06434 (2015). Key ideas: • Replace FC hidden layers with Convolutions • Generator:Fractional-Strided convolutions • Use Batch Normalization after each layer • Inside Generator • Use ReLU for hidden layers • Use Tanh for the output layer
  • 21.
    Latent vectors captureinteresting patterns… Radford, Alec, Luke Metz, and SoumithChintala. "Unsupervised representationlearning withdeep convolutional generative adversarial networks." arXiv:1511.06434 (2015).
  • 22.
    Part 2 • Advantagesof GANs • Training Challenges • Non-Convergence • Mode-Collapse • Proposed Solutions • Supervision with Labels • Mini-Batch GANs • Modification of GAN’s losses • Discriminator (EB-GAN) • Generator (InfoGAN)
  • 23.
    Advantages of GANs •Plenty of existing work on Deep Generative Models • Boltzmann Machine • Deep Belief Nets • Variational AutoEncoders(VAE) • Why GANs? • Sampling (or generation) is straightforward. • Training doesn't involveMaximum Likelihoodestimation. • Robust to Overfitting since Generator never sees the training data. • Empirically, GANs are good at capturing the modes of the distribution. Goodfellow, Ian. "NIPS 2016 Tutorial: Generative Adversarial Networks." arXiv preprint arXiv:1701.00160 (2016).
  • 24.
    Problems with GANs •Probability Distribution is Implicit • Not straightforward to compute P(X). • Thus Vanilla GANs are only good for Sampling/Generation. • Training is Hard • Non-Convergence • Mode-Collapse Goodfellow, Ian. "NIPS 2016 Tutorial: Generative Adversarial Networks." arXiv preprint arXiv:1701.00160 (2016).
  • 25.
  • 26.
    min $ max ' 𝑉 𝐷, 𝐺 •Deep Learning models (in general) involve a single player • The player tries to maximizeits reward (minimizeits loss). • Use SGD (with Backpropagation) to find the optimal parameters. • SGD has convergenceguarantees (under certain conditions). • Problem: With non-convexity,we might convergeto local optima. min $ 𝐿 𝐺 • GANs instead involve two (or more) players • Discriminator is trying to maximizeits reward. • Generator is trying to minimizeDiscriminator’sreward. • SGD was not designed to find the Nash equilibrium of a game. • Problem: We might not converge to the Nash equilibrium at all. Salimans, Tim, et al. "Improved techniques for training gans." Advances in Neural Information Processing Systems. 2016.
  • 27.
    Non-Convergence min 1 max X 𝑉 𝑥, 𝑦 Let𝑉 𝑥, 𝑦 = 𝑥𝑦 • State 1: • State 2: • State 3: • State 4 : • State 5: == State 1 x > 0 y > 0 V > 0 Increase y Decrease x Decrease y Decrease x Decrease y Increase x Increase y Increase x Increase y Decrease x x < 0 y > 0 V < 0 x < 0 y < 0 V > 0 x > 0 y < 0 V < 0 x > 0 y > 0 V > 0
  • 28.
    Non-Convergence min 1 max X 𝑥𝑦 • Z Z1 = −y … Z ZX =x • Z] ZX] = Z Z1 = −𝑦 • Differential equation’ssolutionhas sinusoidal terms • Even with a small learning rate, it will not converge Goodfellow, Ian. "NIPS 2016 Tutorial: Generative Adversarial Networks." arXiv preprint arXiv:1701.00160 (2016).
  • 29.
  • 30.
    Mode-Collapse • Generator failsto output diverse samples Metz, Luke, et al. "Unrolled Generative Adversarial Networks." arXiv preprint arXiv:1611.02163 (2016). Expected Output Target
  • 31.
    Some real examples Reed,S., et al. Generating interpretable images with controllable structure. Technical report, 2016. 2, 2016.
  • 32.
    Some Solutions • Mini-BatchGANs • Supervision with labels • Some recent attempts :- • Unrolled GANs • W-GANs
  • 33.
    Basic (Heuristic) Solutions •Mini-Batch GANs • Supervision with labels
  • 34.
    How to rewardsample diversity? • At Mode Collapse, • Generator produces good samples, but a very few of them. • Thus, Discriminator can’t tag them as fake. • To address this problem, • Let the Discriminator know about this edge-case. • More formally, • Let the Discriminator look at the entire batch instead of single examples • If there is lack of diversity, it will mark the examples as fake • Thus, • Generator will be forced to produce diverse samples. Salimans, Tim, et al. "Improved techniques for training gans." Advances in Neural Information Processing Systems. 2016.
  • 35.
    Mini-Batch GANs • Extractfeatures that capture diversity in the mini-batch • For e.g. L2 norm of the difference between all pairs from the batch • Feed those features to the discriminator along with the image • Feature values will differ b/w diverse and non-diverse batches • Thus, Discriminator will rely on those features for classification • This in turn, • Will force the Generator to match those feature values with the real data • Will generate diverse batches Salimans, Tim, et al. "Improved techniques for training gans." Advances in Neural Information Processing Systems. 2016.
  • 36.
    Basic (Heuristic) Solutions •Mini-Batch GANs • Supervision with labels
  • 37.
    Supervision with Labels •Label information of the real data might help • Empirically generates much better samples Salimans, Tim, et al. "Improved techniques for training gans." Advances in Neural Information Processing Systems. 2016. D Real Fake D Human Fake Car Dog
  • 38.
    Alternate view ofGANs min $ max ' 𝑉 𝐷,𝐺 𝑉 𝐷, 𝐺 = 𝔼1∼3(1) log 𝐷 𝑥 + 𝔼;∼<(;) log 1 − 𝐷 𝐺(𝑧) 𝐷∗ = 𝑎𝑟𝑔max ' 𝑉 𝐷, 𝐺 𝐺∗ = 𝑎𝑟𝑔m𝑖𝑛 $ 𝑉 𝐷, 𝐺 • In this formulation,Discriminator’s strategy was 𝐷 𝑥 → 1, 𝐷 𝐺 𝑧 → 0 • Alternatively, we can flip the binary classification labels i.e. Fake = 1, Real = 0 𝑉 𝐷,𝐺 = 𝔼1∼3(1) log 1 − 𝐷 𝑥 + 𝔼;∼<(;) log 𝐷 𝐺(𝑧) • In this new formulation,Discriminator’s strategy will be 𝐷 𝑥 → 0, 𝐷 𝐺 𝑧 → 1 Zhao, Junbo, Michael Mathieu, and Yann LeCun. "Energy-based generative adversarial network." arXiv preprint arXiv:1609.03126 (2016)
  • 39.
    Alternate view ofGANs (Contd.) • If all we want to encode is 𝐷 𝑥 → 0, 𝐷 𝐺 𝑧 → 1 𝐷∗ = 𝑎𝑟𝑔𝑚𝑎𝑥' 𝔼1∼3(1) log 1 − 𝐷 𝑥 + 𝔼;∼<(;) log 𝐷 𝐺(𝑧) 𝐷∗ = 𝑎𝑟𝑔𝑚𝑖𝑛' 𝔼1∼3 1 log 𝐷 𝑥 + 𝔼;∼<(;) log 1 − 𝐷 𝐺 𝑧 • Now, we can replace cross-entropy with any loss function (Hinge Loss) 𝐷∗ = 𝑎𝑟𝑔𝑚𝑖𝑛' 𝔼1∼3 1 𝐷 𝑥 + 𝔼;∼< ; max 0, 𝑚 − 𝐷 𝐺 𝑧 • And thus, instead of outputtingprobabilities,Discriminator just has to output:- • High values for fake samples • Low values for real samples Zhao, Junbo, Michael Mathieu, and Yann LeCun. "Energy-based generative adversarial network." arXiv preprint arXiv:1609.03126 (2016) We can use this
  • 40.
    Energy-Based GANs • Modifiedgame plans • Generator will try to generate samples with low values • Discriminatorwill try to assign high scores to fake values • Use AutoEncoderinside the Discriminator • Use Mean-Squared Reconstructionerror as 𝑫 𝒙 • High ReconstructionError for Fake samples • Low ReconstructionError for Real samples Zhao, Junbo, Michael Mathieu, and Yann LeCun. "Energy-based generative adversarial network." arXiv preprint arXiv:1609.03126 (2016) 𝐷 𝑥 = ||𝐷𝑒𝑐 𝐸𝑛𝑐 𝑥 − 𝑥||ijk
  • 41.
    More Bedrooms… Zhao, Junbo,Michael Mathieu, and Yann LeCun. "Energy-based generative adversarial network." arXiv preprint arXiv:1609.03126 (2016)
  • 42.
  • 43.
    The Cool Stuff… 3DFaces Chen, X., Duan, Y., Houthooft, R., Schulman, J., Sutskever, I., & Abbeel, P. InfoGAN:Interpretable RepresentationLearning by Information MaximizationGenerative Adversarial Nets, NIPS (2016).
  • 44.
    Chen, X., Duan,Y., Houthooft, R., Schulman, J., Sutskever, I., & Abbeel, P. InfoGAN:Interpretable RepresentationLearning by Information MaximizationGenerative Adversarial Nets, NIPS (2016). 3D Chairs Cool Stuff (contd.)
  • 45.
    How to rewardDisentanglement? Chen, X., Duan, Y., Houthooft, R., Schulman, J., Sutskever, I., & Abbeel, P. InfoGAN:Interpretable RepresentationLearning by Information MaximizationGenerative Adversarial Nets • Disentanglement means individual dimensions independently capturing key attributes of the image • Let’s partition the noise vector into 2 parts :- • z vector will capture slight variations in the image • c vector will capture the main attributes of the image • For e.g. Digit, Angle and Thickness of images in MNIST • If c vector captures the key variations in the image, Will c and 𝒙𝒇𝒂𝒌𝒆 be highly correlated or weakly correlated?
  • 46.
    Recap: Mutual Information •Mutual Information captures the mutual dependence between two variables • Mutual informationbetween two variables 𝑿,𝒀 is defined as: 𝐼 𝑋; 𝑌 = v 𝑝 𝑥, 𝑦 log 𝑝 𝑥, 𝑦 𝑝 𝑥 𝑝 𝑦 1,X 𝐼 𝑋; 𝑌 = 𝐻 𝑋 − 𝐻 𝑋 𝑌 = H Y − H(Y|X)
  • 47.
    InfoGAN • We wantto maximize the mutual information 𝐼 between 𝒄 and 𝐱 = 𝑮(𝒛, 𝒄) • Incorporate in the value function of the minimax game. Chen, X., Duan, Y., Houthooft, R., Schulman, J., Sutskever, I., & Abbeel, P. InfoGAN:Interpretable RepresentationLearning by Information MaximizationGenerative Adversarial Nets, NIPS (2016). min $ max ' 𝑉• 𝐷, 𝐺 = 𝑉 𝐷, 𝐺 − 𝜆 𝐼 𝑐; 𝐺 𝑧, 𝑐
  • 48.
    Mutual Information’s VariationalLower bound 𝐼 𝑐; 𝐺 𝑧, 𝑐 = 𝐻 𝑐 − 𝐻 𝑐 𝐺 𝑧, 𝑐 = 𝔼1 ~ $ ;,• 𝔼•‚ ~ ƒ 𝑐 𝑥 log𝑃 𝑐„ 𝑥 + 𝐻(𝑐) = 𝔼1 ~ $ ;,• 𝐷…†(𝑃| 𝑄 + 𝔼•‚ ~ ƒ 𝑐 𝑥 log𝑄 𝑐„ 𝑥 + 𝐻(𝑐) ≥ 𝔼1 ~ $ ;,• 𝔼•‚ ~ ƒ 𝑐 𝑥 log𝑄 𝑐„ 𝑥 + 𝐻(𝑐) ≥ 𝔼•~ƒ • , 1 ~ $ ;,• 𝐥𝐨𝐠 𝑸(𝒄|𝒙) + 𝐻(𝑐) Chen, X., Duan, Y., Houthooft, R., Schulman, J., Sutskever, I., & Abbeel, P. InfoGAN:Interpretable RepresentationLearning by Information MaximizationGenerative Adversarial Nets, NIPS (2016). InfoGAN 𝐷 𝑄
  • 49.
    Part 3 • ConditionalGANs • Applications • Image-to-Image Translation • Text-to-Image Synthesis • Face Aging • Advanced GAN Extensions • Coupled GAN • LAPGAN – Laplacian Pyramid of Adversarial Networks • Adversarially Learned Inference • Summary
  • 50.
    Conditional GANs Mirza, Mehdi,and Simon Osindero. Conditional generative adversarial nets. arXiv preprint arXiv:1411.1784 (2014). Figure 2 in the original paper. generated conditioned on their class label. 1, 0, 0,0, 0, 0, 0, 0, 0, 0 0, 1, 0,0, 0, 0, 0, 0, 0, 0 0, 0, 1,0, 0, 0, 0, 0, 0, 0 0, 0, 0,1, 0, 0, 0, 0, 0, 0 0, 0, 0,0, 1, 0, 0, 0, 0, 0 0, 0, 0,0, 0, 1, 0, 0, 0, 0 0, 0, 0,0, 0, 0, 1, 0, 0, 0 0, 0, 0,0, 0, 0, 0, 1, 0, 0 0, 0, 0,0, 0, 0, 0, 0, 1, 0 0, 0, 0,0, 0, 0, 0, 0, 0, 1 MNIST digits MNIST digits
  • 51.
    Conditional GANs • Simplemodification to the original GAN framework that conditions the model on additional information for better multi-modal learning. • Lends to many practical applications of GANs when we have explicit supervision available. Mirza, Mehdi, and Simon Osindero. “Conditional generative adversarial nets”. arXiv preprint arXiv:1411.1784 (2014). Image Credit: Figure 2 inOdena, A., Olah, C. and Shlens, J., 2016. Conditional image synthesis withauxiliaryclassifier GANs. arXiv preprint arXiv:1610.09585.
  • 52.
    Part 3 • ConditionalGANs • Applications • Image-to-Image Translation • Text-to-Image Synthesis • Face Aging • Advanced GAN Extensions • Coupled GAN • LAPGAN – Laplacian Pyramid of Adversarial Networks • Adversarially Learned Inference • Summary
  • 53.
    Image-to-Image Translation Isola, P.,Zhu, J. Y., Zhou, T., & Efros, A. A. “Image-to-image translation with conditional adversarial networks”. arXiv preprint arXiv:1611.07004. (2016). Figure 1 in the original paper. Link to an interactive demo of this paper
  • 54.
    Image-to-Image Translation • Architecture:DCGAN-based architecture • Training is conditioned on the images from the source domain. • Conditional GANs provide an effective way to handle many complex domains without worrying about designing structured loss functions explicitly. Isola, P., Zhu, J. Y., Zhou, T., & Efros, A. A. “Image-to-image translation with conditional adversarial networks”. arXiv preprint arXiv:1611.07004. (2016). Figure 2 in the original paper.
  • 55.
    Text-to-Image Synthesis Reed, S.,Akata, Z., Yan, X., Logeswaran, L., Schiele, B., & Lee, H. “Generative adversarial text to image synthesis”. ICML (2016). Figure 1 in the original paper. Motivation Given a text description, generate images closely associated. Uses a conditional GAN with the generator and discriminator being condition on “dense” text embedding.
  • 56.
    Text-to-Image Synthesis Reed, S.,Akata, Z., Yan, X., Logeswaran, L., Schiele, B., & Lee, H. “Generative adversarial text to image synthesis”. ICML (2016). Figure 2 in the original paper. Positive Example: Real Image, Right Text Negative Examples: Real Image, Wrong Text Fake Image, Right Text
  • 57.
    Face Aging withConditional GANs Antipov, G., Baccouche, M., & Dugelay, J. L. (2017). “Face Aging With Conditional Generative Adversarial Networks”. arXiv preprint arXiv:1702.01983. Figure 1 in the original paper. • Differentiating Feature: Uses an Identity Preservation Optimization using an auxiliary network to get a better approximationof the latent code (z*) for an input image. • Latent code is then conditionedon a discrete (one-hot) embedding of age categories.
  • 58.
    Face Aging withConditional GANs Antipov, G., Baccouche, M., & Dugelay, J. L. (2017). “Face Aging With Conditional Generative Adversarial Networks”. arXiv preprint arXiv:1702.01983. Figure 3 in the original paper.
  • 59.
    Conditional GANs Conditional ModelCollapse • Scenario observed when the ConditionalGAN starts ignoring either the code (c) or the noise variables (z). • This limits the diversity of images generated. Mirza, Mehdi, and Simon Osindero. Conditional generative adversarial nets. arXiv preprint arXiv:1411.1784 (2014). Credit?
  • 60.
    Part 3 • ConditionalGANs • Applications • Image-to-Image Translation • Text-to-Image Synthesis • Face Aging • Advanced GAN Extensions • Coupled GAN • LAPGAN – Laplacian Pyramid of Adversarial Networks • Adversarially Learned Inference • Summary
  • 61.
    Coupled GAN • Learninga joint distribution of multi-domain images. • Using GANs to learn the joint distribution with samples drawn from the marginal distributions. • Direct applications in domain adaptation and image translation. Liu, Ming-Yu, and Oncel Tuzel. “Coupled generative adversarial networks”. NIPS (2016). Figure 2 in the original paper.
  • 62.
    Coupled GANs • Architecture Liu,Ming-Yu, and Oncel Tuzel. “Coupled generative adversarial networks”. NIPS (2016). Weight-sharing constraints the network to learn a joint distribution without corresponding supervision. Figure 1 of the original paper.
  • 63.
    Coupled GANs Liu, Ming-Yu,and Oncel Tuzel. “Coupled generative adversarial networks”. NIPS (2016). • Some examples of generating facial images across different feature domains. • Correspondingimages in a column are generate from the same latent code 𝑧 Figure 4 in the original paper. Hair Color Facial Expression Sunglasses
  • 64.
    Laplacian Pyramid ofAdversarial Networks Denton, E.L., Chintala, S. and Fergus, R., 2015. “Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks”. NIPS (2015) Figure 1 in the original paper. (Edited for simplicity) • Based on the Laplacian Pyramid representation ofimages.(1983) • Generate high resolution(dimension)images byusing a hierarchical system ofGANs • Iterativelyincrease image resolution and quality.
  • 65.
    Laplacian Pyramid ofAdversarial Networks Denton, E.L., Chintala, S. and Fergus, R., 2015. “Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks”. NIPS (2015) Figure 1 in the original paper. Image Generation using a LAPGAN • Generator 𝐺• generatesthe base image 𝐼• Ž from random noise input 𝑧•. • Generators (𝐺J,𝐺I,𝐺•)iterativelygenerate the difference image (ℎ ‘) conditionedon previous small image (𝑙). • This difference image is added to an up-scaled version of previous smaller image.
  • 66.
    Laplacian Pyramid ofAdversarial Networks Denton, E.L., Chintala, S. and Fergus, R., 2015. “Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks”. NIPS (2015) Figure 2 in the original paper. Training Procedure: Models at each level are trained independently to learn the required representation.
  • 67.
    Adversarially Learned Inference •Basic idea is to learn an encoder/inferencenetwork along with the generator network. • Consider the following joint distributions over 𝑥 (image) and 𝑧 (latent variables) : 𝑞 𝑥, 𝑧 = 𝑞 𝑥 𝑞(𝑧|𝑥) 𝑝 𝑥, 𝑧 = 𝑝 𝑧 𝑝(𝑥|𝑧) Dumoulin, Vincent, et al. “Adversarially learned inference”. arXiv preprint arXiv:1606.00704 (2016). encoder distribution generator distribution
  • 68.
    Adversarially Learned Inference Dumoulin,Vincent, et al. “Adversarially learned inference”. arXiv preprint arXiv:1606.00704 (2016). min $ max ' 𝔼< 1 [log 𝐷 𝑥, 𝐺; 𝑥 + 𝔼3 1 log 1 − 𝐷 𝐺1 𝑧 , 𝑧 Generator Network Encoder/Inference Network Discriminator Network Figure 1 in the original paper.
  • 69.
    Adversarially Learned Inference •Nash equilibrium yields • Joint: 𝑝 𝑥, 𝑧 ~ 𝑞 𝑥, 𝑧 • Marginals: 𝑝 𝑥 ~ 𝑞 𝑥 and 𝑝 𝑧 ~ 𝑞 𝑧 • Conditionals: 𝑝 𝑥|𝑧 ~ 𝑞(𝑥|𝑧) and 𝑝 𝑧|𝑥 ~ 𝑞 𝑧|𝑥 • Inferred latent representation successfully reconstructed the original image. • Representation was useful in the downstream semi-supervised task. Dumoulin, Vincent, et al. “Adversarially learned inference”. arXiv preprint arXiv:1606.00704 (2016).
  • 70.
    Summary • GANs aregenerative models that are implemented using two stochastic neural network modules: Generator and Discriminator. • Generator tries to generate samples from random noise as input • Discriminatortries to distinguish the samples from Generator and samples from the real data distribution. • Both networksare trained adversarially (in tandem) to fool the other component. In this process, both models become better at their respective tasks.
  • 71.
    Why use GANsfor Generation? • Can be trained using back-propagation for Neural Network based Generator/Discriminator functions. • Sharper images can be generated. • Faster to sample from the model distribution: single forward pass generates a single sample.
  • 72.
    Reading List • Goodfellow,I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair,S., Courville, A.and Bengio, Y. Generative adversarial nets, NIPS (2014). • Goodfellow, Ian NIPS 2016 Tutorial: Generative Adversarial Networks, NIPS (2016). • Radford,A., Metz, L. and Chintala, S., Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv preprint arXiv:1511.06434.(2015). • Salimans, T., Goodfellow, I., Zaremba, W.,Cheung, V., Radford,A., & Chen, X. Improved techniques for training gans. NIPS (2016). • Chen, X., Duan, Y., Houthooft, R., Schulman, J., Sutskever, I., & Abbeel, P. InfoGAN: Interpretable Representation Learning by Information Maximization Generative Adversarial Nets, NIPS (2016). • Zhao, Junbo, Michael Mathieu, and Yann LeCun. Energy-based generative adversarial network. arXiv preprint arXiv:1609.03126(2016). • Mirza, Mehdi, and Simon Osindero.Conditional generative adversarial nets. arXiv preprintarXiv:1411.1784 (2014). • Liu, Ming-Yu, and Oncel Tuzel. Coupled generative adversarial networks. NIPS (2016). • Denton, E.L., Chintala, S. and Fergus, R., 2015.Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks. NIPS (2015) • Dumoulin, V., Belghazi, I., Poole, B., Lamb, A., Arjovsky,M., Mastropietro, O., & Courville, A. Adversarially learned inference. arXiv preprint arXiv:1606.00704 (2016). Applications: • Isola, P., Zhu, J. Y., Zhou, T., & Efros,A. A. Image-to-image translation with conditional adversarial networks. arXiv preprintarXiv:1611.07004.(2016). • Reed, S., Akata, Z., Yan, X., Logeswaran, L., Schiele, B., & Lee, H. Generative adversarial text to image synthesis. JMLR (2016). • Antipov,G., Baccouche, M., & Dugelay, J. L. (2017).Face Aging With Conditional Generative Adversarial Networks. arXiv preprintarXiv:1702.01983.
  • 73.