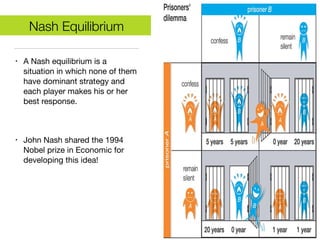
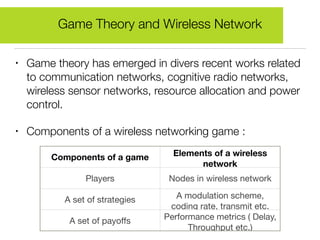
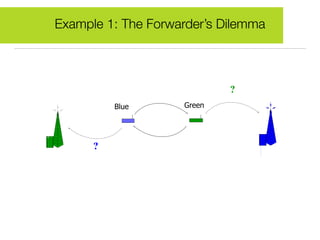
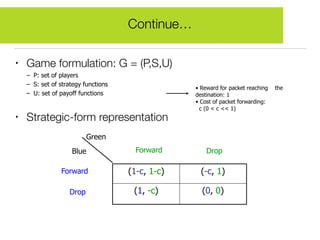
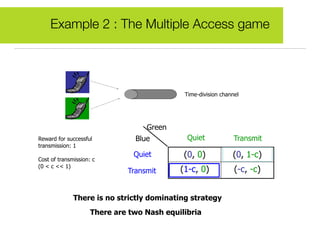
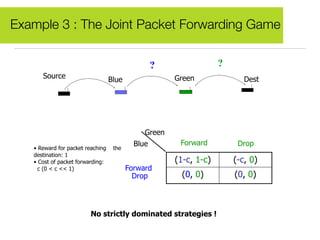
Game theory is a mathematical tool used to describe strategic interactions between decision-makers. It involves players, strategies, and payoffs. A Nash equilibrium exists when no player can benefit by unilaterally changing their strategy given other players' strategies. The document provides examples of how game theory applies to wireless networks, including a forwarder's dilemma game about forwarding packets, a multiple access game about transmitting, and a joint packet forwarding game.

1. Game Theory and Learning for
Wireless Network
Author : Pooya Sagharchi Ha

2. • What is The Game Theory ?
• Nash Equilibrium
• Game Theory and Wireless Network
• Examples on Game Theory in Wireless Network
Agenda

3. • Developed in 1950 by mathematicians John von
Neumann and economist Oskar Morgenstern.
• Game theory is concerned with situations in which
decision-makers interact with one another.
• and in which the happiness of each participant with the
outcome depends not just on his or her own decisions
but on the decision made by everyone.
• A mathematical tool used to describe and solve games
depending on 3 basic elements:
What is Game Theory?

4. Nash Equilibrium
• A Nash equilibrium is a
situation in which none of them
have dominant strategy and
each player makes his or her
best response.
• John Nash shared the 1994
Nobel prize in Economic for
developing this idea!

5. • Players :
• Players are the decision takers in the game
• Strategies:
• Define a plan of action for every contingency
• Payoffs :
• a utility function decides the all possible outcomes for
each player
Continue…

6. • Game theory has emerged in divers recent works related
to communication networks, cognitive radio networks,
wireless sensor networks, resource allocation and power
control.
• Components of a wireless networking game :
Game Theory and Wireless Network
Components of a game Elements of a wireless
network
Players Nodes in wireless network
A set of strategies A modulation scheme,
coding rate, transmit etc.
A set of payoffs Performance metrics ( Delay,
Throughput etc.)

8. Example 1: The Forwarder’s Dilemma
?
?
Blue Green

9. • Game formulation: G = (P,S,U)
– P: set of players
– S: set of strategy functions
– U: set of payoff functions
• Strategic-form representation
Continue…
• Reward for packet reaching the
destination: 1
• Cost of packet forwarding:
c (0 < c << 1)
(1-c, 1-c) (-c, 1)
(1, -c) (0, 0)
Blue
Green
Forward
Drop
Forward Drop

10. Example 2 : The Multiple Access game
Time-division channel
Reward for successful
transmission: 1
Cost of transmission: c
(0 < c << 1)
There is no strictly dominating strategy
(0, 0) (0, 1-c)
(1-c, 0) (-c, -c)
Blue
Green
Quiet
Transmit
Quiet Transmit
There are two Nash equilibria

11. Example 3 : The Joint Packet Forwarding Game
?
Blue GreenSource Dest
?
No strictly dominated strategies !
• Reward for packet reaching the
destination: 1
• Cost of packet forwarding:
c (0 < c << 1)
(1-c, 1-c) (-c, 0)
(0, 0) (0, 0)
Blue
Green
Forward
Drop
Forward Drop

12. “Any Questions ?! .”