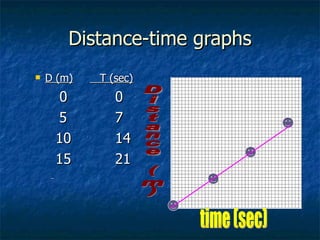
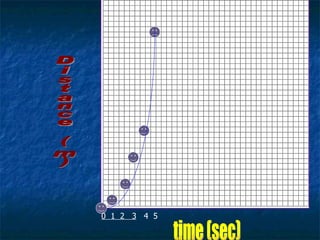
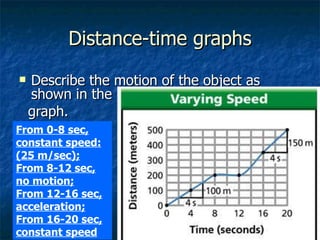
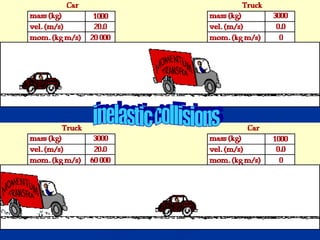
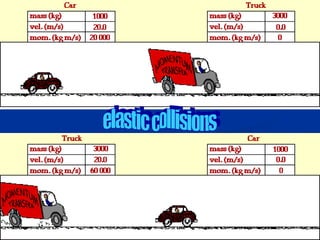
The document discusses key concepts in motion including frames of reference, speed, velocity, acceleration, momentum, Newton's laws of motion, gravity, weight, and air resistance. It provides examples and practice problems for each concept. Key terms like force, mass, distance, and time are defined throughout in the context of describing and quantifying different types of motion.

1. Fourth six weeks review

2. Frames of Reference Object or point from which motion is determined Most common is Earth Motion is a change in position relative to a frame of reference

3. What is motion? If you are standing in one place, and your friend walks by you, are you moving relative to your friend? Is your friend moving relative to you? Is either of you moving relative to the earth?

4. Answer: You are moving relative to your friend, and your friend is moving relative to you! You (the Joker) are not moving relative to the earth, but your friend is. You are both moving relative to the sun! Who is moving relative to the computer screen?

5. Speed Speed = Distance ÷ Time D_ S T Example: A car travels 300km in 6 hours. What is the speed of the car?

6. Answer: Speed = distance ÷ time Speed = 300km ÷ 6 hours Speed = 50km/hr

7. More practice 1. How far can a plane travel if it flies 800km/hr for 9 hours? 2. How long does it take a ship to go 500 km if it travels at a speed of 50km/hr?

8. Answer 1. D S T D 800 9 800km ▪ 9hrs = 7200km hr

9. Answer 2. D S T 500 50 T 500km ÷ 50km = 10 hrs hr

10. Velocity Speed in a given direction. What is the velocity of a boat that travels from St. Peter to Mankato (10 miles) in 15 minutes?

11. Answer Speed = distance ÷ time Speed = 10 miles ÷ 15 minutes Speed = 0.67 mi/min Velocity = 0.67 mi/min South

12. Distance-time graphs D (m) T (sec) 0 0 5 7 10 14 15 21 time (sec) Distance (m)

13. Was your graph a straight line? A distance-time graph which is a straight line indicates constant speed . In constant speed, the object does not speed up or slow down. The acceleration is zero.

14. time (sec) Distance (m) 0 1 2 3 4 5

15. Was your graph a curve? A graph that curves on a distance-time graph shows that the object is accelerating

16. Distance-time graphs Describe the motion of the object as shown in the graph. From 0-8 sec, constant speed: (25 m/sec); From 8-12 sec, no motion; From 12-16 sec, acceleration; From 16-20 sec, constant speed

17. What does your graph look like? Constant speed will be a horizontal line on a speed time graph. If the speed decreases , the line will slant down . If the speed increases , the line will slant up .

18. Acceleration Change in velocity Can be change in speed or direction Acceleration = ∆V/ ∆T ∆ V a t

19. Acceleration problem A roller coaster’s velocity at the top of a hill is 10m/s. Two seconds later it reaches the bottom of the hill with a velocity of 26m/s. What is the acceleration of the roller coaster?

20. Answer Acceleration = ∆V/ ∆T a = 26m/s – 10m/s 2 s a = 16m/s 2s a = 8m/s/s or 8m/s 2

21. More acceleration problems 1. A car accelerates at a rate of 20mi/hr/s. How long does it take to reach a speed of 80 mi/hr? 2. A car travels at 60 miles per hour around a curve. Is the car accelerating? 3. A car travels in a straight line at 60mi/hr. Is the car accelerating?

22. Answers: 1. ∆V 80mi/hr a t 20mi/hr/s t 4sec = t 2. yes! Because it’s changing direction! 3. no! It’s not changing speed or direction!

23. Deceleration Negative acceleration Example: A car slows from 60mi/hr to 20mi/hr in 4 seconds. What is its acceleration?

24. Answer: Acceleration = ∆V/ ∆T Acceleration = Vf – Vi t a = 20mi/hr – 60mi/hr 4 s a = -40mi/hr 4s a = -10mi/hr/s

25. Momentum Momentum = Mass x Velocity Which has more momentum: a 300lb football player moving at 5m/s or a 200lb quarterback moving at 10m/s?

26. Answer: Momentum of the 300lb player is (300 lbs/2.2 lbs) x 5 m/s= 681.8 kg-m/s Momentum of the quarterback is (200lbs/2.2 lbs) x 10m/s = 909.1 kg-m/s The quarterback has a greater momentum!

29. inelastic collisions

30. Inelastic collision

31. elastic collisions

32. Elastic collision

33. Two dimensional collision

34. Momentum problems 2 cars are heading east, car A is traveling 30mi/hr, car B is traveling 60mi/hr. Each car weighs 2000lbs. What is the momentum of car A? What is the momentum of car B? If car B crashes into car A, what is the total momentum?

35. Answers: P=mv Car A’s momentum = 30mi/hr x (2000lbs/2.2lbs) P A = 27272.73 kg-mi/hr east Car B’s momentum = 60mi/hr x (2000lbs/2.2lbs) P B = 54545.46 kg-mi/hr east Total momentum = P A + P B = 27272.73 + 54545.46 = 81818.19 kg-mi/hr east

36. Another momentum problem! Car X is traveling 30mi/hr east, car Y is traveling 60mi/hr west. Each car weighs 2000lbs. What is the momentum of car X? What is the momentum of car Y? If car X crashes into car Y, what is the total momentum?

37. Answers: P=mv Car X’s momentum = 30mi/hr x (2000lbs/2.2 lbs) Px = 27272.73 kg-mi/hr east Car Y’s momentum = 60mi/hr x (2000lbs/2.2lbs) P Y = 54545.45 kg-mi/hr west Total momentum = P Y - P X = 54545.45-27272.73 = 27272.72 kg-mi/hr west

38. Newton's Laws of Motion

39. FORCE = Any push or pull which causes something to move or change its speed or direction What is a Force?

40. Forces can be BALANCED or UNBALANCED Balanced forces are equal in size and opposite in direction Unbalanced forces are not equal in size and/or opposite in direction. If the forces on an object are UNBALANCED, we say a NET force results. What is a Force? Amusement Park Forces

41. First Law : An object at rest stays at rest or an object in motion, stays in motion (in the same direction/at the same speed) unless acted upon by an unbalanced force Also called the law of inertia Newton's Laws of Motion

42. Newtons’s 1 st Law and You Don’t let this be you. Wear seat belts. Because of inertia, objects (including you) resist changes in their motion. When the car going 80 km/hour is stopped by the brick wall, your body keeps moving at 80 m/hour.

43. Examples of Newton’s 1 st Law

44. Why then, do we observe every day objects in motion slowing down and becoming motionless seemingly without an outside force? It’s a force we sometimes cannot see – friction.

45. Friction is a force that occurs when 2 surfaces oppose each other.

46. Types of friction Static- Friction that acts on something that is not moving Sliding - Force resulting when pushing or pulling an object over a surface. Rolling - Contact is reduced because of rollers or wheels or ball bearings Fluid - Resistance from a “liquid” or air.

47. 2 nd Law F = m x a

48. Second law : The greater the force applied to an object, the more the object will accelerate . It takes more force to accelerate an object with a lot of mass than to accelerate something with very little mass. Newton's Laws of Motion The player in black had more acceleration thus he hit with a greater amount of force

49. 2 nd Law When mass is in kilograms and acceleration is in m/s/s, the unit of force is in newtons (N). One newton is equal to the force required to accelerate one kilogram of mass at one meter/second/second.

50. 2 nd Law (F = m x a) How much force is needed to accelerate a 1400 kilogram car 2 meters per second/per second? Write the formula F = m x a Fill in given numbers and units F = 1400 kg x 2 meters per second/second Solve for the unknown 2800 kg-meters/second/second or 2800 N

51. Newton’s 2 nd Law proves that different masses accelerate to the earth at the same rate, but with different forces. We know that objects with different masses accelerate to the ground at the same rate. However, because of the 2 nd Law we know that they don’t hit the ground with the same force. F = ma 98 N = 10 kg x 9.8 m/s/s F = ma 9.8 N = 1 kg x 9.8 m/s/s

52. Examples of Newton’s 2nd Law

53. Check Your Understanding 1. What acceleration will result when a 12 N net force applied to a 3 kg object? A 6 kg object? 2. A net force of 16 N causes a mass to accelerate at a rate of 5 m/s 2 . Determine the mass. 3. How much force is needed to accelerate a 66 kg skier 1 m/sec/sec? 4. What is the force on a 1000 kg elevator that is falling freely at 9.8 m/sec/sec?

54. Check Your Understanding 1. What acceleration will result when a 12 N net force applied to a 3 kg object? 12 N = 3 kg x 4 m/s/s 2. A net force of 16 N causes a mass to accelerate at a rate of 5 m/s 2 . Determine the mass. 16 N = 3.2 kg x 5 m/s/s 3. How much force is needed to accelerate a 66 kg skier 1 m/sec/sec? 66 kg-m/sec/sec or 66 N 4. What is the force on a 1000 kg elevator that is falling freely at 9.8 m/sec/sec? 9800 kg-m/sec/sec or 9800 N

55. Third law : For every action force, there is an equal and opposite reaction force. (Forces are always paired) Newton's Laws of Motion

56. 3 rd Law There are two forces resulting from this interaction - a force on the chair and a force on your body. These two forces are called action and reaction forces.

57. 3 rd Law Flying gracefully through the air, birds depend on Newton’s third law of motion. As the birds push down on the air with their wings, the air pushes their wings up and gives them lift.

59. Examples of Newton’s 3 rd Law

60. GRAVITY : An attraction force between all masses Newton’s universal law of gravitation : Every object in the universe exerts a gravitational attraction to all other objects in the universe The amount of gravitational force depends upon the mass of the objects and the distance between the objects What is Gravity?

61. The greater the mass, the greater the force The greater the distance , the less the force Acceleration due to gravity = 9.8 m/s/s or 9.8 m/s 2 What is Gravity? Gravity in Space

63. Weight is a measure of the gravitational force between two objects The greater the mass the greater the force (weight) Measured in units called Newtons (N)

64. Weightlessness – free from the effects of gravity

65. Air resistance : The force of air exerted on a falling object The air pushes up as gravity pulls down Dependent upon the size and speed of the object When the air resistance equals the force of gravity, terminal velocity is reached Terminal velocity is the highest velocity that an object will reach as it falls