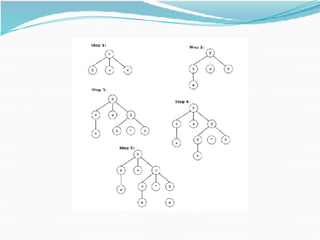
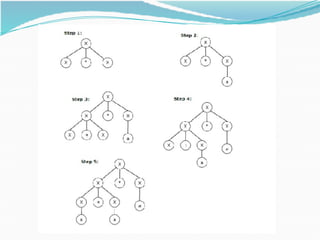
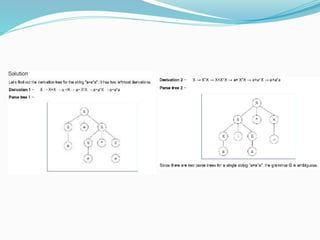
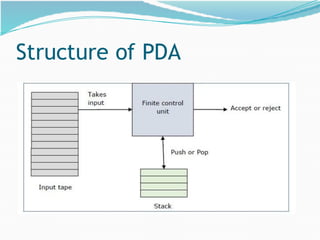
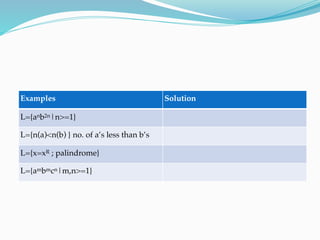
This document provides an overview of context-free grammars and pushdown automata. It begins with definitions and examples of context-free grammars, including their components, derivations, parse trees, ambiguity, and applications. It then covers pushdown automata, defining them as finite state machines with a stack. It discusses the two types of acceptability in PDAs - final state and empty stack acceptability. Examples of languages recognized by PDAs are provided. The document concludes with how to convert between context-free grammars and pushdown automata, including examples of converting a CFG to a PDA and vice versa. It also briefly discusses deterministic pushdown automata.

1. UNIT-3
Context-Free Grammars
Prepared By:
K Lakshmi Sravani
Assistant Professor

2. Syllabus
Context-Free Grammars: Definition of Context-Free
Grammars,
Derivations Using a Grammar, Leftmost and Rightmost Derivations,
the Language of a Grammar, Sentential Forms, Parse
Tress,
Applications of Context-Free Grammars, Ambiguity in
Grammars
and Languages.
Push Down Automata: Definition of the Pushdown Automaton, the
Languages of a PDA, Equivalence of PDA's and CFG's,
Acceptance
by final state, Acceptance by empty stack, Deterministic Pushdown
Automata. From CFG to PDA, From PDAto CFG.

3. Context-Free Grammars(CFG)
● AGFG is a set of recursive rewriting productions
used to generate patterns of strings.
● It has 4 components
● G= (V,T,P,S)
● V is set of variables/Non Terminals
● T is set of terminal symbols
● P is set of productions
● S is start symbol

4. Example 1:
E->E+E
E->E*E
E->id
● Solution:
V={E}
T={id,+,*}
S={E}
P= {E->E+E, E->E*E, E->id}

5. Example 2:
● The grammar for Palindrome over input alphabet {0,1} or
L={wwR|w in {0,1}, WR is reversal of w}
● G={V,T,P,S}
● S->E, S->0, S->1, S->0S0, S->1S1
● Derive string 010010
● S
● 0S0.
● 01S10
● 010S010.
● 010S010.
010010
010010
010010
010010

6. Example 3

7. Example 4:

8. Derivation Tree
A derivation tree or parse tree is an ordered rooted tree that
graphically represents the semantic information a string derived
from a context-free grammar.
Representation Technique
Root vertex - Must be labeled by the start symbol
Vertex - Labeled by a non-terminal symbol.
Leaves − Labeled by a terminal symbol or ε

9. There are two different approaches to draw a derivation tree
Top-downApproach −
Starts with the starting symbol S
•
• Goes down to tree leaves using productions
Bottom-upApproach −
Starts from tree leaves
•
• Proceeds upward to the root which is the starting symbol S

10. Leftmost and Rightmost Derivation
Leftmost derivation −
Aleftmost derivation is obtained by applying production to the
leftmost variable in each step.
Rightmost derivation
Arightmost derivation is obtained by applying production to the
rightmost variable in each step.

11. Leftmost Derivation
Example
Let any set of production rules in a CFG be
X → X+X | X*X |X| a
The leftmost derivation for the string "a+a*a" may be
X → X+X → a+X → a + X*X → a+a*X → a+a*a

13. Rightmost Derivation
Example
Let any set of production rules in a CFG be
X → X+X | X*X |X| a
The Rightmost derivation for the string "a+a*a" may be
X → X*X → X*a → X+X*a → X+a*a → a+a*a

15. Example 2
● Construct the derivation tree for string aabbabba
from CFG given by
● S->aB|bA
● A->a|aS|bAA
● B->b|bS|aBB

16. Ambiguous grammar
If a context free grammar G has more than one derivation tree
for
some string w ∈ L(G), it is called an ambiguous
grammar.
There exist multiple right-most or left-most derivations for some
string generated from that
grammar.
Problem
Check whether the grammar G with production rules −
X → X+X | X*X |X| a
is ambiguous or not.

18. Example 2
● S->aAB
● A->bC|cd
● C->cd
● B->c/d
● Check ambiguous or not

19. Part 2

20. Push Down Automata
A PDA can be formally described as a 7-tuple (Q, ∑, S/ ,, δ, q0, I/Z0, F) −
Q is the finite number of states
∑ is input alphabet
S/ is stack symbols
q0 is the initial state. (q0 ∈ Q)
I/Z0 is the initial stack top symbol (I ∈ S)
F is a set of accepting states (F ∈ Q)
δ is the transition function
•

21. Basically a pushdown automaton is −
"Finite state machine" + "a stack”
Apushdown automaton has three components −
• an input tape,
• a control unit, and
• a stack with infinite size.
The stack head scans the top symbol of the stack.
Astack does two operations −
Push − a new symbol is added at the top.
Pop- the top symbol is read and removed.

22. Structure of PDA

23. Example
● The following diagram shows a transition in a PDA from a state
q1 to state q2, labeled as a,b → c
● This means at state q1, if we encounter an input string ‘a’ and
top symbol of the stack is ‘b’, then we pop ‘b’, push ‘c’ on top
of the stack and move to state q2.

24. Two ways of Acceptability
● There are two different ways to define PDA
acceptability.
1. Final state acceptability
2. Empty Stack Acceptability

25. Final State Acceptability
● In final state acceptability, a PDA accepts a string when,
after reading the entire string, the PDA is in a final state.
From the starting state, we can make moves that end up
in a final state with any stack values. The stack values
are irrelevant as long as we end up in a final state.
● For a PDA (Q, ∑, S, δ, q0, I/Z0, F), the language
accepted by the set of final states F is −
● L(PDA) = {w | (q0, w, Z0) ⊢* (q, ε, x), q ∈ F}
● for any input stack string x.

26.
Empty Stack Acceptability
● Here a PDA accepts a string when, after reading the
entire string, the PDA has emptied its stack.
● For a PDA (Q, ∑, S, δ, q0, Z0, F), the language
accepted by the empty stack is −
● L(PDA) = {w | (q0, w, Z0) ⊢* (q, ε, ε), q ∈ Q}

27. Examples:

29. Examples Solution
L={anb2n|n>=1}
L={n(a)<n(b) } no. of a’s less than b’s
L={x=xR ; palindrome}
L={ambmcn|m,n>=1}

30. Conversion of CFG to PDA
● Let L = L(G).
● Construct PDA P such that N(P) = L.
● P has:
● One state q.
● Input symbols = terminals of G.
● Stack symbols = all symbols of G.
● Start symbol = start symbol of G.
Rules:
1> Non Terminal Symbol
If A -> α is a production of G, then δ(q, ε, A) =(q, α).
2>Terminal Symbol
δ(q, a, a) = (q, ε)

31. Example

32. Example

33. Conversion of PDA to CFG

34. Example

35. Deterministic PDA