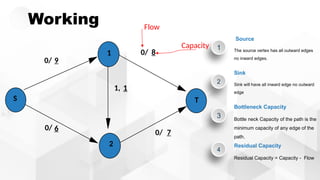
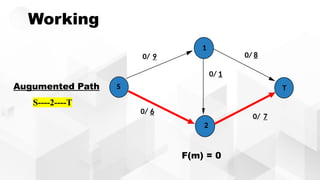
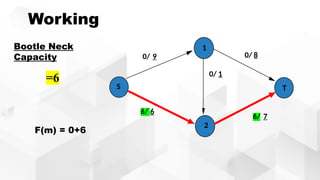
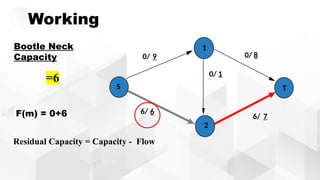
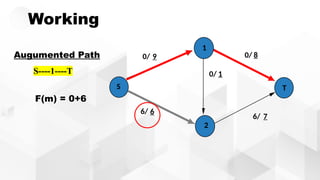
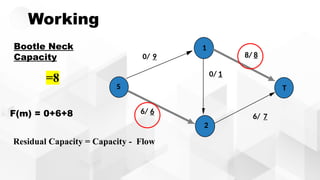
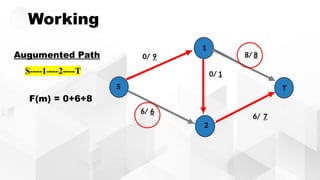
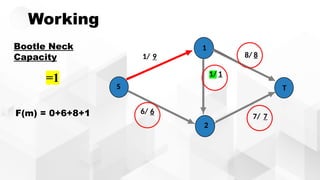
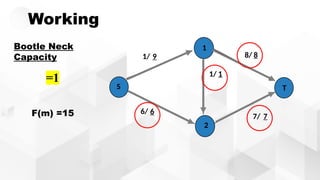
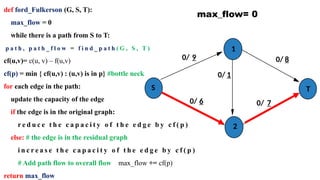
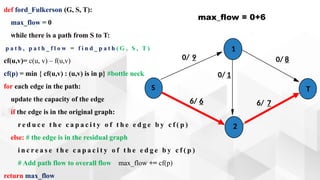
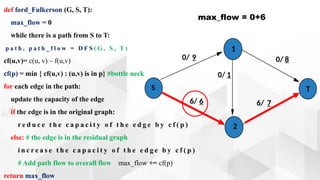
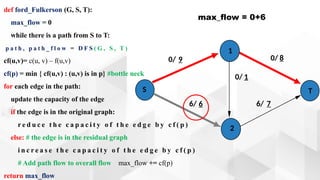
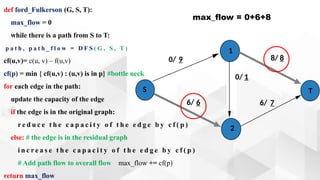
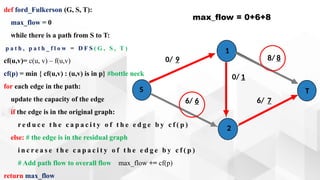
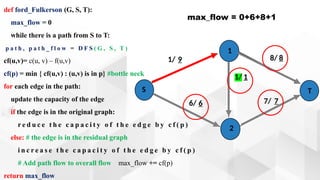
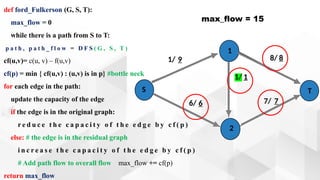
The document discusses the Ford-Fulkerson algorithm, a greedy approach for finding the maximum flow in a network by calculating bottleneck and residual capacities. It outlines its applications, including water distribution and bipartite matching, and highlights its advantages such as simplicity and flexibility, as well as disadvantages like inefficiency with real limits and issues with loops. The algorithm's pseudocode is provided along with its time complexity analysis.

1. Limitations
IV
Applications
II
I
Algorithm
&
Time
Complexity
I
I
I
Introduction
Contents

2. Limitations
IV
Applications
II
I
Algorithm
&
Time
Complexity
I
I
I
Introduction
Contents

3. Limitations
IV
Applications
II
I
Algorithm
&
Time
Complexity
I
I
I
Introduction

4. Introduction
01
PART

5. Ford
Fulkerson
Ford-Fulkerson algorithm is a
greedy approach for Calculating
the maximum flow in a network.

6. Net Work Flow
Network flow refers to the movement of data, traffic, or
other forms of communication through a network, such as
a computer network, transportation network, or social
network. It involves the transfer of information or
resources from one node or vertex to another, often
following specific paths or routes.

7. 1 The source vertex has all outward edges
no inward edges.
Source
2 Sink will have all inward edge no outward
edge
Sink
3 Bottle neck Capacity of the path is the
minimum capacity of any edge of the
path.
Bottleneck Capacity
4
Residual Capacity = Capacity - Flow
Residual Capacity
Working
S
1
2
T
0/ 9
0/ 8
1, 1
0/ 7
0/ 6
Flow
Capacity

8. Working
0/ 9
0/ 1
0/ 7
0/ 6
S
1
2
T
0/ 8
Augumented Path
S----2----T
F(m) = 0

9. Working
0/ 9
0/ 1
6/ 7
6/ 6
S
1
2
T
0/ 8
Bootle Neck
Capacity
=6
F(m) = 0+6

10. Working
0/ 9
0/ 1
6/ 7
6/ 6
S
1
2
T
0/ 8
Bootle Neck
Capacity
=6
F(m) = 0+6
Residual Capacity = Capacity - Flow

11. Working
0/ 9
0/ 1
6/ 7
6/ 6
S
1
2
T
0/ 8
Augumented Path
S----1----T
F(m) = 0+6

12. Working
0/ 9
0/ 1
6/ 7
6/ 6
S
1
2
T
8/ 8
Bootle Neck
Capacity
=8
F(m) = 0+6+8
Residual Capacity = Capacity - Flow

13. Working
0/ 9
0/ 1
6/ 7
6/ 6
S
1
2
T
8/ 8
Augumented Path
S----1----2----T
F(m) = 0+6+8

14. Working
1/ 9
1/ 1
7/ 7
6/ 6
S
1
2
T
8/ 8
Bootle Neck
Capacity
=1
F(m) = 0+6+8+1

15. Working
1/ 9
1/ 1
7/ 7
6/ 6
S
1
2
T
8/ 8
Bootle Neck
Capacity
=1
F(m) =15

16. Pseudocode
&
Time Complexity
02
PART

17. def ford_Fulkerson (G, S, T):
max_flow = 0
while there is a path from S to T:
p a t h , p a t h _ f l o w = f i n d _ p a t h ( G , S , T )
cf(u,v)= c(u, v) – f(u,v)
cf(p) = min { cf(u,v) : (u,v) is in p} #bottle neck
for each edge in the path:
update the capacity of the edge
if the edge is in the original graph:
r e d u c e t h e c a p a c i t y o f t h e e d g e b y c f ( p )
else: # the edge is in the residual graph
i n c r e a s e t h e c a p a c i t y o f t h e e d g e b y c f ( p )
# Add path flow to overall flow max_flow += cf(p)
return max_flow
S
1
2
T
max_flow= 0
0/ 9
0/ 1
0/ 7
0/ 6
0/ 8

18. def ford_Fulkerson (G, S, T):
max_flow = 0
while there is a path from S to T:
p a t h , p a t h _ f l o w = f i n d _ p a t h ( G , S , T )
cf(u,v)= c(u, v) – f(u,v)
cf(p) = min { cf(u,v) : (u,v) is in p} #bottle neck
for each edge in the path:
update the capacity of the edge
if the edge is in the original graph:
r e d u c e t h e c a p a c i t y o f t h e e d g e b y c f ( p )
else: # the edge is in the residual graph
i n c r e a s e t h e c a p a c i t y o f t h e e d g e b y c f ( p )
# Add path flow to overall flow max_flow += cf(p)
return max_flow
S
1
2
T
0/ 9
0/ 1
6/ 7
6/ 6
0/ 8
max_flow = 0+6

19. def ford_Fulkerson (G, S, T):
max_flow = 0
while there is a path from S to T:
p a t h , p a t h _ f l o w = D F S ( G , S , T )
cf(u,v)= c(u, v) – f(u,v)
cf(p) = min { cf(u,v) : (u,v) is in p} #bottle neck
for each edge in the path:
update the capacity of the edge
if the edge is in the original graph:
r e d u c e t h e c a p a c i t y o f t h e e d g e b y c f ( p )
else: # the edge is in the residual graph
i n c r e a s e t h e c a p a c i t y o f t h e e d g e b y c f ( p )
# Add path flow to overall flow max_flow += cf(p)
return max_flow
S
1
2
T
0/ 9
0/ 1
6/ 7
6/ 6
0/ 8
max_flow = 0+6

20. def ford_Fulkerson (G, S, T):
max_flow = 0
while there is a path from S to T:
p a t h , p a t h _ f l o w = D F S ( G , S , T )
cf(u,v)= c(u, v) – f(u,v)
cf(p) = min { cf(u,v) : (u,v) is in p} #bottle neck
for each edge in the path:
update the capacity of the edge
if the edge is in the original graph:
r e d u c e t h e c a p a c i t y o f t h e e d g e b y c f ( p )
else: # the edge is in the residual graph
i n c r e a s e t h e c a p a c i t y o f t h e e d g e b y c f ( p )
# Add path flow to overall flow max_flow += cf(p)
return max_flow
max_flow = 0+6
0/ 9
0/ 1
6/ 7
6/ 6
S
1
2
T
0/ 8

21. def ford_Fulkerson (G, S, T):
max_flow = 0
while there is a path from S to T:
p a t h , p a t h _ f l o w = D F S ( G , S , T )
cf(u,v)= c(u, v) – f(u,v)
cf(p) = min { cf(u,v) : (u,v) is in p} #bottle neck
for each edge in the path:
update the capacity of the edge
if the edge is in the original graph:
r e d u c e t h e c a p a c i t y o f t h e e d g e b y c f ( p )
else: # the edge is in the residual graph
i n c r e a s e t h e c a p a c i t y o f t h e e d g e b y c f ( p )
# Add path flow to overall flow max_flow += cf(p)
return max_flow
max_flow = 0+6+8
0/ 9
0/ 1
6/ 7
6/ 6
S
1
2
T
8/ 8

22. def ford_Fulkerson (G, S, T):
max_flow = 0
while there is a path from S to T:
p a t h , p a t h _ f l o w = D F S ( G , S , T )
cf(u,v)= c(u, v) – f(u,v)
cf(p) = min { cf(u,v) : (u,v) is in p} #bottle neck
for each edge in the path:
update the capacity of the edge
if the edge is in the original graph:
r e d u c e t h e c a p a c i t y o f t h e e d g e b y c f ( p )
else: # the edge is in the residual graph
i n c r e a s e t h e c a p a c i t y o f t h e e d g e b y c f ( p )
# Add path flow to overall flow max_flow += cf(p)
return max_flow
max_flow = 0+6+8
0/ 9
0/ 1
6/ 7
6/ 6
S
1
2
T
8/ 8

23. def ford_Fulkerson (G, S, T):
max_flow = 0
while there is a path from S to T:
p a t h , p a t h _ f l o w = D F S ( G , S , T )
cf(u,v)= c(u, v) – f(u,v)
cf(p) = min { cf(u,v) : (u,v) is in p} #bottle neck
for each edge in the path:
update the capacity of the edge
if the edge is in the original graph:
r e d u c e t h e c a p a c i t y o f t h e e d g e b y c f ( p )
else: # the edge is in the residual graph
i n c r e a s e t h e c a p a c i t y o f t h e e d g e b y c f ( p )
# Add path flow to overall flow max_flow += cf(p)
return max_flow
max_flow = 0+6+8+1
1/ 9
1/ 1
7/ 7
6/ 6
S
1
2
T
8/ 8

24. def ford_Fulkerson (G, S, T):
max_flow = 0
while there is a path from S to T:
p a t h , p a t h _ f l o w = D F S ( G , S , T )
cf(u,v)= c(u, v) – f(u,v)
cf(p) = min { cf(u,v) : (u,v) is in p} #bottle neck
for each edge in the path:
update the capacity of the edge
if the edge is in the original graph:
r e d u c e t h e c a p a c i t y o f t h e e d g e b y c f ( p )
else: # the edge is in the residual graph
i n c r e a s e t h e c a p a c i t y o f t h e e d g e b y c f ( p )
# Add path flow to overall flow max_flow += cf(p)
return max_flow
max_flow = 15
1/ 9
1/ 1
7/ 7
6/ 6
S
1
2
T
8/ 8

25. Time Complexity

26. d e f f o r d _ F u l k e r s o n ( G , S , T ) : To t a l = O ( F * E )
m a x _ f l o w = 0 O ( 1 )
w h i l e t h e r e i s a p a t h f r o m S t o T: O ( f )
p a t h , p a t h _ f l o w = D F S ( G , S , T ) O ( E )
c f ( u , v ) = c ( u , v ) – f ( u , v )
c f ( p ) = m i n { c f ( u , v ) : ( u , v ) i s i n p } # b o t t l e n e c k
f o r e a c h e d g e i n t h e p a t h :
u p d a t e t h e c a p a c i t y o f t h e e d g e
i f t h e e d g e i s i n t h e o r i g i n a l g r a p h :
r e d u c e t h e c a p a c i t y o f t h e e d g e b y c f ( p ) O ( 1 )
e l s e : # t h e e d g e i s i n t h e r e s i d u a l g r a p h
i n c r e a s e t h e c a p a c i t y o f t h e e d g e b y c f ( p ) O ( 1 )
# A d d p a t h f l o w t o o v e r a l l f l o w m a x _ f l o w + = c f ( p ) O ( 1 )

27. Application
03
PART

28. Water Distribution Pipeline:
In the context of a water distribution pipeline, it could be used to determine the
maximum amount of water that can flow from a source (like a reservoir) to various
destinations (like homes or businesses) through a network of pipes while respecting
capacity constraints.
For example, imagine a water distribution system with a source reservoir, several
intermediate junctions, and multiple endpoints (e.g., homes, factories). Each pipe
connecting these points has a maximum capacity of water it can carry.

29. Bipartite matching problem:
The Bipartite Matching Problem is a graph theory problem where the goal is to find
the maximum matching in a bipartite graph. This means finding the largest possible
set of edges with no common vertices.
For example, consider a scenario where you have a set of students and a set of
projects, and you want to match each student with exactly one project based on their
preferences. This can be represented as a bipartite graph, with students on one side
and projects on the other, and edges indicating preferences.

30. Advantages
04
PART

31. 1. Easy to Understand: The algorithm is simple to understand and apply due to its
clear idea.
2. Flexible: It may be used to solve a wide range of flow network problems,
including network flow optimization and transportation.
3. Efficient in Some Cases: It can be fairly efficient in some situations if capacities
are integers and there are a finite number of augmenting paths.

32. Disadvantages
05
PART

33. 1. Not Always Efficient: If the limits are real, the procedure could take a while to
find the maximum flow in the worst-case.
2. Dependent on Initial Flow: Selecting the right initial flow can have an impact on
how well the algorithm performs, but doing so can be difficult.
3. May Not Handle Loops Well: The algorithm could fail or could return inaccurate
results if it finds loops in the flow network.

34. Thanks