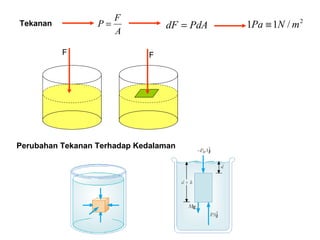
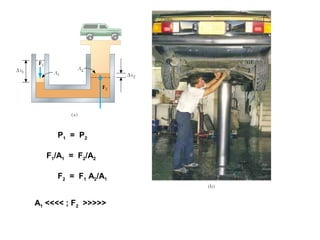
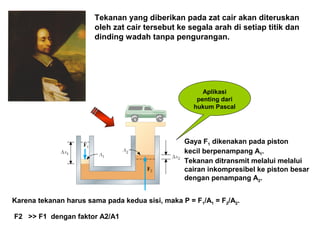
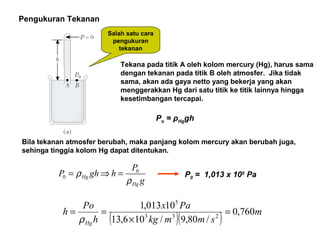
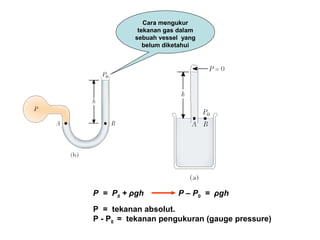
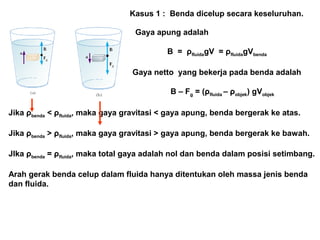
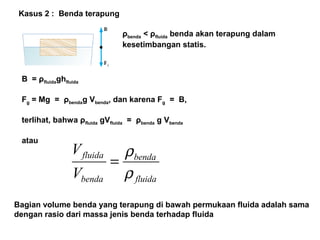
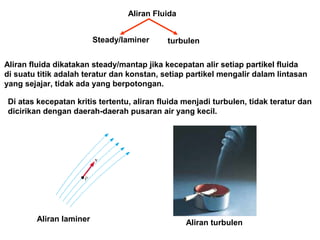
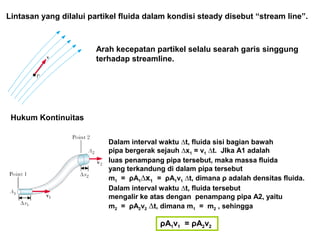
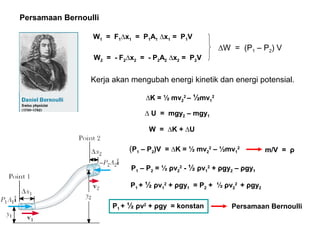
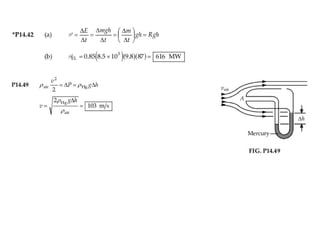
Dokumen ini menjelaskan konsep dasar mekanika fluida, termasuk hukum pascal, prinsip archimedes, dan aliran fluida, serta interaksi antara tekanan, gaya, dan massa dalam fluida. Hukum kontinuitas dan persamaan Bernoulli juga dibahas untuk menunjukkan bagaimana tekanan dan kecepatan fluida saling terkait. Selain itu, faktor seperti viskositas dan perbedaan densitas mempengaruhi perilaku fluida dalam berbagai kondisi.

2. Fluida adalah sekumpulan molekul yang secara acak (random) tersusun dan
terikat satu sama lain oleh gaya-gaya kohesif yang lemah dan oleh gaya-gaya
yang diberikan oleh dinding-dinding wadah (container).
Mekanika Fluida
Statika Fluida Dinamika Fluida
Fluida
Cairan
(liquid)
Gas

4. F F
Tekanan
A
F
P = PdAdF =
2
/11 mNPa ≡
Perubahan Tekanan Terhadap Kedalaman

5. Tekanan yang diberikan oleh cairan pada permukaan bagian
bawah adalah adalah P dan tekanan pada bagian atas adalah
Po. Karena itu, gaya ke atas yang diberikan oleh fluida pada
bagian bawah adalah PA dan gaya ke bawah yang diberikan
pada bagian atas adalah PoA.
Massa fluida dalam silinder adalah M = ρV = ρAh, sehingga,
berat cairan dalam silinder adalah Mg = ρAhg.
Karena silinder adalah setimbang, total gaya yang bekerja
padanya harus nol.
Dengan menganggap arah ke atas adalah arah y positif, terlihat bahwa
ghPP
AhgAPPA
AhgAPPA
jMgjAPjPAF
ρ
ρ
ρ
+=
=−
=−−
=−−=∑
0
0
0
0
0
0ˆˆˆ
Tekanan pada suatu titik dalam zat cair
mempunyai nilai yang lebih besar dari Po,
dengan selisih sebesar ρgh.
Tekanan pada setiap titik pada ketinggian yang
sama adalah sama, tidak bergantuk pada bentuk
wadahnya.

6. P1 = P2
F1/A1 = F2/A2
F2 = F1 A2/A1
A1 <<<< ; F2 >>>>>

7. Tekanan yang diberikan pada zat cair akan diteruskan
oleh zat cair tersebut ke segala arah di setiap titik dan
dinding wadah tanpa pengurangan.
Aplikasi
penting dari
hukum Pascal
Gaya F1 dikenakan pada piston
kecil berpenampang A1.
Tekanan ditransmit melalui melalui
cairan inkompresibel ke piston besar
dengan penampang A2.
Karena tekanan harus sama pada kedua sisi, maka P = F1/A1 = F2/A2.
F2 >> F1 dengan faktor A2/A1

8. Dengan mendesain tekanan hidraulik dengan
pengaturan luas penampang piston A1 dan A2,
dapat diperoleh gaya output yang besar
dengan gaya input yang kecil.
Karena volume liquid adalah tetap, maka volum
liquid yang terdorong ke bawah di sisi kiri
gambar adalah sama dengan volum yang
terdorong ke atas di sisi kanan gambar.
A1 ∆x1 = A2 ∆x2
F1/F2 = A1/A2 = ∆x2/∆x1
A1/A2 = ∆x2/∆x1
F1∆x1 = F2 ∆x2
Kerja yang dilakukan pada input piston adalah sama dengan kerja yang
dilakukan pada output piston.
Hukum kekekalan energi

9. Pengukuran Tekanan
Salah satu cara
pengukuran
tekanan
Tekana pada titik A oleh kolom mercury (Hg), harus sama
dengan tekanan pada titik B oleh atmosfer. Jika tidak
sama, akan ada gaya netto yang bekerja yang akan
menggerakkan Hg dari satu titik ke titik lainnya hingga
kesetimbangan tercapai.
Po = ρHggh
Bila tekanan atmosfer berubah, maka panjang kolom mercury akan berubah juga,
sehinga tinggia kolom Hg dapat ditentukan.
g
P
hghP
Hg
Hg
ρ
ρ 0
0 =⇒= P0 = 1,013 x 105
Pa
( )( ) m
smmkg
Pax
h
Po
h
Hg
760,0
/80,9/106,13
10013,1
233
5
=
×
==
ρ

10. Cara mengukur
tekanan gas dalam
sebuah vessel yang
belum diketahui
P = P0 + ρgh P – P0 = ρgh
P = tekanan absolut.
P - P0 = tekanan pengukuran (gauge pressure)

11. Gaya Apung dan Prinsip Archimedes
Besarnya gaya apung selalu sama dengan berat
fluida yang dipindahkan oleh sebuah benda yang
dicelupkan padanya.
B = buoyant force = gaya apung

12. Untuk memahami gaya apung, perhatikan gambar ini.
Tekanan Pb pada bagian bawah kubus lebih besar dari
tekanan di bagian atas Pt sebesar ρfluidagh, dimana h adalah
tinggi kubus dan ρfluida adalah kerapatan massa (density)
fluida. Tekanan pada bagian bawah kubus menyebabkan
gaya ke atas sama dengan ρbA, dimana A adalah luas
permukaan bawah. Tekanan pada bagian atas kubus
menyebabkan gaya ke bawah PtA.
Resultan dari kedua gaya ini adalah gaya apung B :
B = (Pb – Pt)A = (ρfluidagh)A = ρfluidagV
Dimana V = volume fluida yang dipindahkan oleh balok.
Karena perkalian ρf;luidaV adalah sama dengan massa fluida yang dipindahkan
oleh benda, maka terlihat bahwa
B = Mg
Dimana Mg adalah berat fluida yang dipindahkan oleh balok.
Ini sesuai dengan hukum Archimedes yang didiskusikan di atas.

13. Kasus 1 : Benda dicelup secara keseluruhan.
Gaya apung adalah
B = ρfluidagV = ρfluidagVbenda
Gaya netto yang bekerja pada benda adalah
B – Fg = (ρfluida – ρobjek) gVobjek
Jika ρbenda < ρfluida, maka gaya gravitasi < gaya apung, benda bergerak ke atas.
Jika ρbenda > ρfluida, maka gaya gravitasi > gaya apung, benda bergerak ke bawah.
JIka ρbenda = ρfluida, maka total gaya adalah nol dan benda dalam posisi setimbang.
Arah gerak benda celup dalam fluida hanya ditentukan oleh massa jenis benda
dan fluida.

14. Kasus 2 : Benda terapung
ρbenda < ρfluida benda akan terapung dalam
kesetimbangan statis.
B = ρfluidaghfluida
Fg = Mg = ρbendag Vbenda, dan karena Fg = B,
terlihat, bahwa ρfluida gVfluida = ρbenda g Vbenda
atau
fluida
benda
benda
fluida
V
V
ρ
ρ
=
Bagian volume benda yang terapung di bawah permukaan fluida adalah sama
dengan rasio dari massa jenis benda terhadap fluida

16. Aliran fluida dikatakan steady/mantap jika kecepatan alir setiap partikel fluida
di suatu titik adalah teratur dan konstan, setiap partikel mengalir dalam lintasan
yang sejajar, tidak ada yang berpotongan.
Aliran Fluida
Steady/laminer turbulen
Di atas kecepatan kritis tertentu, aliran fluida menjadi turbulen, tidak teratur dan
dicirikan dengan daerah-daerah pusaran air yang kecil.
Aliran laminer Aliran turbulen

17. Unsur viskisotas umumnya digunakan dalam uraian aliran fluida untuk
mencirikan tingkat gesekan internal dalam fluida. Gaya gesekan internal atau
gaya viscous, diandaikan dengan resistansi dari dua lapisan berdekatan yang
bergerak relatif satu terhadap yang lain.
Viskositas menyebabkan sebagian energi kinetik fluida diubah menjadi energi
dalam (internal energy).
Mekanisme ini sama halnya dengan benda yang meluncur di permukaan datar
tanpa kehilangan energi kinetik.
Karena gerakan fluida pada kenyataannya sangat kompleks dan tidak mudah
difahami, kita buat beberapa penyederhanaan pendekatan aliran fluida yang
ideal dengan asmsi :
1. Fluida adalah non viscous, tanpa gesekan.
2. Alirannya steady.
3. Fluida incompressible (tidak termampatkan), density/kerapatan massa
adalah konstan.
4. Aliran irrotational, tidak ada momentum anguler di sekitar titik tertentu

18. Lintasan yang dilalui partikel fluida dalam kondisi steady disebut “stream line”.
Arah kecepatan partikel selalu searah garis singgung
terhadap streamline.
Hukum Kontinuitas
Dalam interval waktu ∆t, fluida sisi bagian bawah
pipa bergerak sejauh ∆x1 = v1 ∆t. JIka A1 adalah
luas penampang pipa tersebut, maka massa fluida
yang terkandung di dalam pipa tersebut
m1 = ρA1∆x1 = ρA1v1 ∆t, dimana ρ adalah densitas fluida.
Dalam interval waktu ∆t, fluida tersebut
mengalir ke atas dengan penampang pipa A2, yaitu
m2 = ρA2v2 ∆t, dimana m1 = m2 , sehingga
ρA1v1 = ρA2v2

19. Persamaan kontinuitas untuk fluida
A1v1 = A2v2
“Hasil kali dari luas dan kecepatan fluida pada semua titik di sepanjang pipa
adalah konstan untuk suatu fluida incompressible”
A1v1 = A2v2

20. W1 = F1∆x1 = P1A1 ∆x1 = P1V
W2 = - F2∆x2 = - P2A2 ∆x2 = P2V
∆W = (P1 – P2) V
Kerja akan mengubah energi kinetik dan energi potensial.
∆K = ½ mv2
2
– ½mv1
2
∆ U = mgy2 – mgy1
W = ∆K + ∆U
(P1 – P2)V = ∆K = ½ mv2
2
– ½mv1
2
m/V = ρ
P1 – P2 = ½ ρv2
2
- ½ ρv1
2
+ ρgy2 – ρgy1
P1 + ½ ρv1
2
+ ρgy1 = P2 + ½ ρv2
2
+ ρgy2
P1 + ½ ρv2
+ ρgy = konstan Persamaan Bernoulli
Persamaan Bernoulli

21. P1 + ½ ρv2
+ ρgy = konstan
Pernyataan ini menunjukkan bahwa tekanan fluida berkurang dengan bertambahnya
kecepatan fluida. Lagi pula, tekanan akan berkurang dengan bertambah besarnya
elevasi. Hal ini akan menjelaskan mengapa tekanan dari kerangan pada lantai atas dari
bangunan tinggi lebih lemah dibandingkan dengan tekanan kerangan di lantai bawah.
Jika v1 = v2 = 0, persamaan di atas menjadi
P1 – P2 = ρg(y2 – y1) = ρgh
Persamaan paling atas diperoleh untuk fluida incompressible, prilaku umum dari tekanan
terhadap kecepatan adalah benar, bahkan untuk gas, tekanan berkurang dengan
bertambahnya kecepatan.