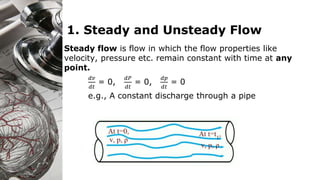
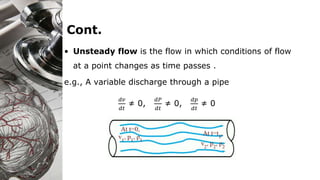
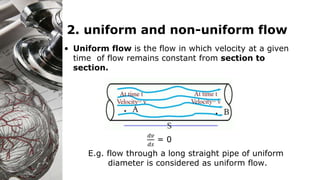
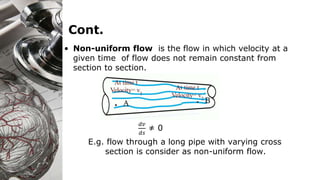
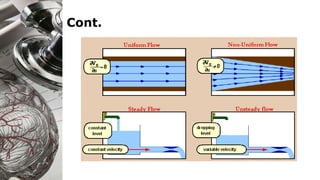
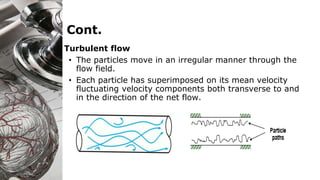
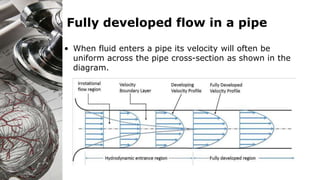
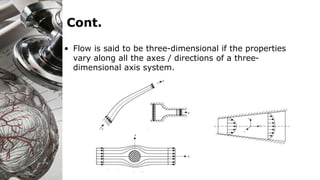
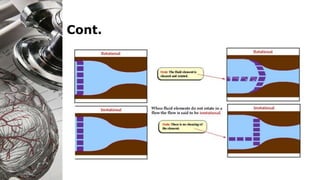
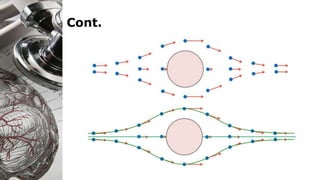
Here are the key steps to solve this problem: 1) Given: Flow rate Q = 34 Lps = 0.034 m3/s Pipe diameter D = 0.1 m Water properties at 50°F: ρ = 1000 kg/m3, μ = 1.12 centipoise 2) Calculate Reynolds number: Re = ρVD/μ = (1000 kg/m3)×(0.034 m3/s)×(0.1 m)/(1.12×10-3 kg/m-s) = 3000 3) The flow is turbulent for Re > 2000. 4) Entrance length for turbulent flow: Lh = 4.4D(

1. CHAPTER 2
Fluid Mechanics
Session 2: Fluid Dynamics

2. Learning outcome
At the end of this chapter and having completing the
essential readings and activities, the students should be
able to:
• explain concepts necessary to analyse fluids in motion
• Identify differences between different flow types
• Demonstrate different flow patterns of fluid

3. Fluid Dynamics
• Fluid dynamics is the branch of applied science that is
concerned with the movement of liquids and gases
• American Heritage Dictionary:Fluid dynamics is one of
two branches of fluid mechanics, which is the study of
fluids and how forces affect them.

4. Basics of Fluid Flow
• The movement of liquids and gases is generally referred
to as "flow," It involves the motion of a fluid subjected
to unbalanced forces
for example, water moving through a channel or pipe, or
over a surface
• Flow is defined as the quantity of fluid that
passes a point per unit time.
• It can be represented by the following equation
Flow(F)= Quantity(q)/Time(t)

5. Types of flow
• Depending upon properties of flow
- steady and unsteady flow
- uniform and non-uniform flow
- Laminar and turbulent flow
- One, two and three-dimensional flow
- Rotational and irrotational flow
• Depending upon fluid properties
- compressible and incompressible flow
- Viscous and inviscid flow

6. 1. Steady and Unsteady Flow
Steady flow is flow in which the flow properties like
velocity, pressure etc. remain constant with time at any
point.
𝑑𝑣
𝑑𝑡
= 0,
𝑑𝑃
𝑑𝑡
= 0,
𝑑𝑝
𝑑𝑡
= 0
e.g., A constant discharge through a pipe

7. Cont.
• Unsteady flow is the flow in which conditions of flow
at a point changes as time passes .
e.g., A variable discharge through a pipe
𝑑𝑣
𝑑𝑡
≠ 0,
𝑑𝑃
𝑑𝑡
≠ 0,
𝑑𝑝
𝑑𝑡
≠ 0

8. 2. uniform and non-uniform flow
• Uniform flow is the flow in which velocity at a given
time of flow remains constant from section to
section.
𝑑𝑣
𝑑𝑠
= 0
E.g. flow through a long straight pipe of uniform
diameter is considered as uniform flow.

9. Cont.
• Non-uniform flow is the flow in which velocity at a
given time of flow does not remain constant from
section to section.
𝑑𝑣
𝑑𝑠
≠ 0
E.g. flow through a long pipe with varying cross
section is consider as non-uniform flow.

10. Cont.

11. Cont.
Steady uniform flow:
• Conditions: do not change with position in the stream
or with time.
• Example: the flow of water in a pipe of constant
diameter at constant velocity.
Steady non-uniform flow:
• Conditions: change from section to section in the
stream but do not change with time.
• Example: flow in a pipe with constant velocity at the
inlet-velocity and will change as you move along the
length of the pipe toward the exit.

12. Cont.
Unsteady uniform flow:
• At a given instant in time the conditions at every point
are the same, but will change with time.
• Example: a pipe of constant diameter connected to a
pump pumping at a constant rate which is then
switched off.
Unsteady non-uniform flow:
• Every condition of the flow may change from point to
point and with time at every point.
• Example: waves in a channel.

13. 3. Laminar and Turbulent flow
Laminar flow
• All the particles proceed along smooth parallel paths
and all particles on any path will follow without
deviation.
Typical
particles
path

14. Cont.
Turbulent flow
• The particles move in an irregular manner through the
flow field.
• Each particle has superimposed on its mean velocity
fluctuating velocity components both transverse to and
in the direction of the net flow.

15. Cont.
Transition Flow
• exists between laminar and turbulent flow.
• In this region, the flow is very unpredictable and often
changeable back and forth between laminar and
turbulent states.

16. Reynold number
• Prof. Osborne Reynolds conducted the experiment to
demonstrate the existence of laminar and turbulent
flow.
• Reynold number is the ratio of inertia force to viscous
force
• Denoted by ‘Re’
• Re =
𝐼𝑛𝑒𝑟𝑡𝑖𝑎 𝑓𝑜𝑟𝑐𝑒
𝑣𝑖𝑠𝑐𝑜𝑢𝑠 𝑓𝑜𝑟𝑐𝑒
=
𝑝𝑣𝑑
𝑢
where ρ = density, v = mean velocity, d = diameter and
µ = viscosity

17. Cont.
• Reynolds number, Re, is a non-dimensional number.
• It can be interpreted that when the inertial forces
dominate over the viscous forces (when the fluid is
flowing faster and Re is larger) then the flow is
turbulent.
• When the viscous forces are dominant (slow flow, low
Re) they are sufficient enough to keep all the fluid
particles in line, then the flow is laminar

18. Sample problem 1
Water at 20°C flow with average velocity of
2cm/s inside a circular pipe. Determine flow
type if the pipe diameter,
a) 2 cm,
b) 15 cm, and
c) 30 cm
PH20=1000kg/m3
u=1.002 x 10-3 kg/ms

19. Sample Problem 2
Water at 20°C flow in a circular pipe of 3.5
cm diameter. Determine the range for the
average velocity so the flow is always
transition flow.
PH20=1000kg/m3
u=1.002 x 10-3 kg/ms

20. Fully developed flow in a pipe
• When fluid enters a pipe its velocity will often be
uniform across the pipe cross-section as shown in the
diagram.

21. Cont.
• Near the entrance, the fluid in the centre of the pipe
isn’t affected by the friction between fluid and pipe walls
• As the flow proceeds down the pipe, the effect of the
wall friction moves in toward the pipe centre, until the
pattern of velocity variation across the pipe (called the
velocity profile) becomes constant.
• The entrance portion of the pipe, where the velocity
profile is changing is called the entrance region, and the
flow after that entrance region is called "fully developed
flow."

22. Estimating the Entrance Length
• The length of the hydrodynamic entry region along the
pipe is called the hydrodynamic entry length. It is a
function of Reynolds number of the flow.
• In case of laminar flow, this length is given by
Lh,laminar=0.05ReD
• But in the case of turbulent flow,
Lh, turbulent = 4.4D(Re1/6)

23. Sample problem 3
Water at 20°C flow with average velocity of
2cm/s inside a circular pipe. calculate the
entry length if the pipe diameter is ,
a) 2 cm
b) 30 cm

24. 4. One, Two and Three-
dimensional Flow
• Although in general all fluids flow three-dimensionally,
with pressures and velocities and other flow properties
varying in all directions, in many cases the greatest
changes only occur in two directions or even only in one.
In these cases changes in the other direction can be
effectively ignored making analysis much more simple.

25. Cont.
• Flow is said to be one-dimensional if the properties vary
only along one axis /be constant with respect to other
two directions of a three/
• Flow is said to be two-dimensional if the properties vary
only along two axes / directions and will be constant
with respect to other direction of a three-dimensional
axis system.

26. Cont.
• Flow is said to be three-dimensional if the properties
vary along all the axes / directions of a three-
dimensional axis system.

27. 5. Rotational and Irrotational Flow
• In rotational the flow in which the fluid particle while
flowing along stream lines, also rotate about their own
axis is called as rotational flow.
• In irrotational The flow in which the fluid particle while
flowing along streamlines, do not rotate about their own
axis is called as irrotational flow.

28. Cont.

29. 6. Compressible and incompressible
flow
• Flow is said to be Incompressible if the fluid density
doesn’t change along the flow direction and is
compressible if the fluid density varies along the flow
direction.

30. 7.Viscous and inviscid flow
• Flow is said to be Inviscid if the fluid have no viscosity
and is viscous if the fluid experience viscous property.
Ideal fluid flow
We make four simplifying assumptions in our treatment of
fluid flow to make the analysis easier:
1. The fluid is inviscid
2. The flow is steady
3. The fluid is incompressible
4. The flow is irrotational

31. Flow patterns of fluid
The flow velocity is the basic description of how a fluid
moves in time and space. In analyzing fluid flow it is
useful to visualize the flow pattern. The following are flow
patterns in a fluid
• Path line
• Stream Line
• Streak Line
• Stream Tube

32. Cont.
1. Pathline: It is trace made by single particle over a
period of time.
2. Streakline: It is the locus of fluid particles that have
passed sequentially through a prescribed point in the flow.
It is an instantaneous picture of the position of all particles
inflow that have passed through a given point.

33. Cont.
3. Streamline: are lines that are tangent to the
velocity field.
• At all points the direction of the streamline is the
direction of the fluid velocity: this is how they are
defined. Close to the wall the velocity is parallel to the
wall so the streamline is also parallel to the wall.

34. Cont.

35. Cont.
Character of Streamlines
• Because the fluid is moving in the same direction as the
streamlines, fluid can not cross a streamline.
• Streamlines can not cross each other. If they were to
cross this would indicate two different velocities at the
same point. This is not physically possible.
The above point implies that any particles of fluid starting
on one streamline will stay on that same streamline
throughout the fluid.

36. Cont.
4. Streamtube
• A useful technique in fluid flow analysis is to consider
only a part of the total fluid in isolation from the rest.
• This can be done by imagining a tubular surface formed
by streamlines along which the fluid flows.
• This tubular surface is known as a streamtube.

37. Flow Rate
Mass flow rate
• Measuring the weight of the fluid in the bucket and
dividing this by the time taken to collect this fluid gives
a rate of accumulation of mass. This is know as the
mass flow rate.
mass flow rate = mass of fluid
time taken to collect the fluid

38. Cont.
Volume flow rate(discharge)
• The discharge is the volume of fluid flowing per unit
time. Multiplying this by the density of the fluid gives us
the mass flow rate.

39. Discharge and mean velocity.
• If the area of cross section of the pipe at point X is A,
and the mean velocity here is um . During a time t, a
cylinder of fluid will pass point X with a volume A× um
×t. The volume per unit time (the discharge) will thus
be

40. Cont.
• Note how carefully we have called this the mean
velocity. This is because the velocity in the pipe is not
constant across the cross section.
• Crossing the center line of the pipe, the velocity is zero
at the walls, increasing to a maximum at the center then
decreasing symmetrically to the other wall.
• This variation across the section is known as the velocity
profile or distribution. A typical one is shown in the
figure

41. Sample Problem 4
- An empty bucket weighs 2.0 kg. After 7 seconds
of collecting water the bucket weighs 8.0 kg,
what is the mass flow rate
- If the density of the fluid in the above question
is 850 kg/m3 what is the volume per unit time
(the discharge in L/s)?
- If we know the mass flow is 1.7 kg/s, how long
will it take to fill a container with 8 kg of fluid?

42. Sample Problem 5
If the cross-section area, A, is 1.2 x 10-3 m2
and the discharge, Q is 2.4 L/s, what is the
mean velocity, of the fluid?

43. Sample problem 6
• Consider flow of 34 Lps of water at 50o F
through a 10cm diameter pipe. What
would the entrance length be for this
flow?
The density and viscosity of water at 50oF
are:
ρ = 1000kg/m3
μ =1.12centipoise.