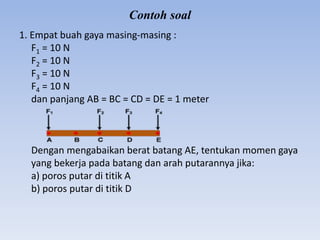
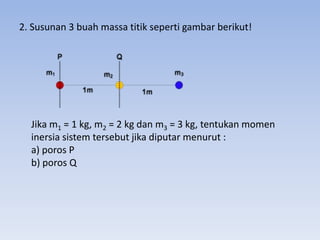
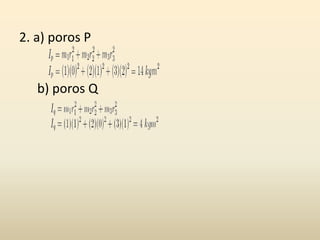Dokumen ini membahas tentang momen inersia, yaitu tingkat kesulitan benda untuk diputar atau dihentikan. Terdapat penjelasan mengenai jenis-jenis momen inersia untuk benda diskrit dan benda tegar, serta rumus-rumus yang terkait. Selain itu, terdapat contoh soal untuk menghitung momen gaya dan momen inersia sistem massa.

1. Nama Kelompok:
1. Aini Ulin Na’mah (03)
2. Asyharudin Hanif (05)
3. Dimas Adji Bagoes Sajiwo (08)
4. Martha Eka Dzulliyanti (19)
5. Safita Ardiana (27)
6. Siti Mughollah (30)
7. Yuni Alia Putri (35)

2. Pengertian
Momen Inersia
Momen inersia adalah tingkat
kesulitan sebuah benda diputar
ketika sedang diam, atau tingkat
kesulitan benda yang sedang
berputar untuk dihentikan.Makin
sulit sebuah benda diputar pada
porosnya, maka makin besar
momen inersianya. Makin mudah
sebuah benda diputar pada
porosnya, maka makin kecil
momen inersianya.

3. Jenis Momen Inersia
1. Momen Inersia Benda Diskrit (Partikel)
 Kecepatan linear dinyatakan dengan ω adalah kecepatan sudut. Oleh
karena itu, besar energi kinetik rotasi partikel dapat dinyatakan sebagai
berikut.
 Dari persamaan di atas, diperoleh nilai mr2 yang menyatakan momen
inersia dari partikel yang bergerak melingkar.
 Dengan demikian, momen inersia sebuah partikel sebanding dengan
massa partikel dan kuadrat jarak antara partikel dan sumbu putarnya.
Momen inersia merupakan besaran skalar yang memiliki satuan kgm2.

4.  Jika ada satu benda yang diputar seperti gambar A, maka persamaan
momen inersia menjadi:
I=mR2
 Jika ada lebih dari satu benda, maka persamaan momen inersia menjadi:
I=∑mR2

5. Momen Inersia beberapa benda yang diketahui

6. 2. Momen Inersia Benda Tegar
 Benda tegar ialah benda yang ketika diberi gaya padanya, bentuknya
tidak berubah.
Contohnya: bola pejal, bola berongga, silinder pejal, silinder
berongga, batang.
 Persamaan Momen Inersia pada benda tegar adalah
I= kmR2
Nilai k tergantung pada bentuk/jenis benda, seperti:
Silinder pejal k=1/2
Silinder berongga k=1
Bola pejal k=2/5
Bola berongga k=2/3
Batang (jika diputar di ujung) k=1/3
Batang (jika diputar di tengah) k=1/12

7. Momen Inersia Benda Tegar dengan massa
terdistribusi kontinu
 Jika benda tegar memiliki distribusi massa yang
kontinu, seperti silinder pejal atau pelat, kita
perlu mengitung momen inersia dengan
metode integraL untuk menghitung
penjumlahan.

8. Contoh soal
1. Empat buah gaya masing-masing :
F1 = 10 N
F2 = 10 N
F3 = 10 N
F4 = 10 N
dan panjang AB = BC = CD = DE = 1 meter
Dengan mengabaikan berat batang AE, tentukan momen gaya
yang bekerja pada batang dan arah putarannya jika:
a) poros putar di titik A
b) poros putar di titik D

9. 2. Susunan 3 buah massa titik seperti gambar berikut!
Jika m1 = 1 kg, m2 = 2 kg dan m3 = 3 kg, tentukan momen
inersia sistem tersebut jika diputar menurut :
a) poros P
b) poros Q

10. Pembahasan
1. a) poros putar di titik A
Putaran searah jarum jam.
b) poros putar di titik D
Putaran berlawanan arah dengan jarum jam

11. 2. a) poros P
b) poros Q