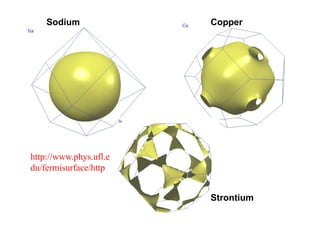
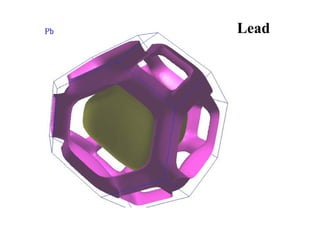
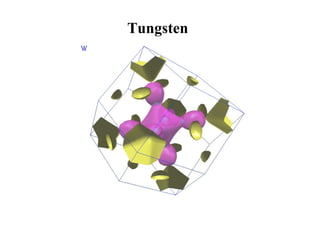
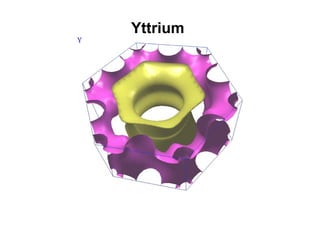
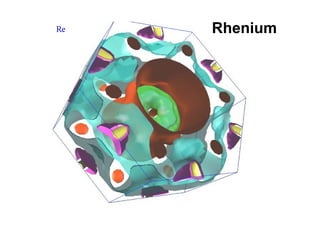
This document discusses Fermi surfaces and band structure calculations in solid state physics. It begins by explaining that band structure calculations give the energy-momentum relationship E(k) for electrons in solids. The dynamics of electrons are determined by E(k), particularly at the Fermi surface. The form and complexity of the Fermi surface depends on factors like overlapping bands. Brillouin zones are constructed to describe the periodic nature of crystal momentum. Metals have a Fermi energy EF, and the Fermi surface is the surface in k-space enclosing states below EF. The Fermi surface need not be a sphere when states are not free electrons. Examples of Fermi surfaces for different materials like sodium, copper, and palladium

1. Solid State Theory
Solid State Theory
Physics 545
Physics 545
Fermi Surfaces
Fermi Surfaces

2. F i f d El t
Fermi surfaces and Electron
dynamics
dynamics
¾Band structure calculations give E(k)
¾Band structure calculations give E(k)
¾E(k) determines the dynamics of the electrons
¾It is E(k) at the Fermi Surface that is important
¾Form of Fermi surface is important
¾Form of Fermi surface is important
¾Fermi surface can be complicated due to
overlapping bands
overlapping bands.

3. Constructing Brillouin Zones
2D Square lattice. BZ constructed from the perpendicular
bisectors of the vectors joining a reciprocal lattice point
t i hb i l tti i t
to neighbouring lattice points 2π/a
1st B. Z.
2ndB. Z.

4. The Fermi Metals have a Fermi energy E
Surface
Metals have a Fermi energy, EF.
The Fermi Temperature,TF, is the
temperature at which kBTF = EF
temperature at which kBTF = EF.
All the free electron states within
a Fermi sphere in k-space are
a Fermi sphere in k space are
filled up to a Fermi wavevector,kF.
The surface of this sphere is
The surface of this sphere is
called the Fermi surface.
On the Fermi surface the free
electrons have a Fermi velocity vF
= hkF/me.
A Fermi surface still exists when the states are not free
A Fermi surface still exists when the states are not free
electron states but it need not be a sphere.

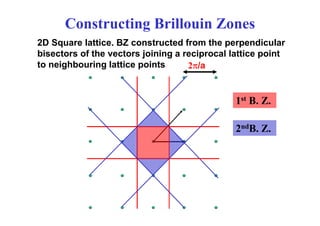
5. Brillouin Zones and Fermi Surfaces
Empty Lattice model (limit of weak
Empty Lattice model (limit of weak
lattice potential):
States are Bloch states.Independent
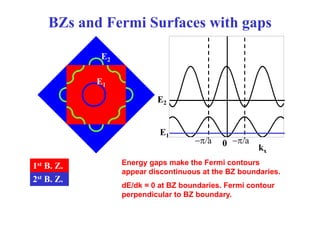
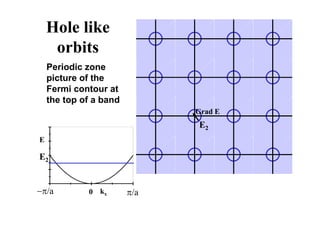
E E2
States are Bloch states.Independent
states have k-vectors in first BZ.
No energy gaps at the BZ boundaries.
E1
kx π/a
−π/a 0
ky
[100]
kx = ky
E1
E2
y
E2
1
E1
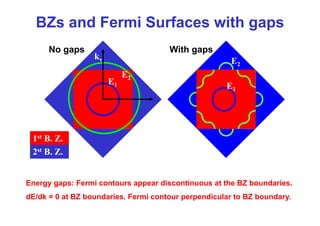
1st B Z
k
−21/2π/a 0 21/2π/a
[110]
2st B. Z.
1st B. Z.

6. Fermi Contours in reduced Zone
E2
PLUS
PLUS
Parts of Fermi circle
moved into 1st BZ
1st B. Z. moved into 1st BZ
from 2nd BZ
2st B. Z.
. .
Reduced Zone scheme
Extended Zone scheme

7. Fermi Contours
i i di Z
in periodic Zone
E2
1st B Z
2st B. Z.
1st B. Z.

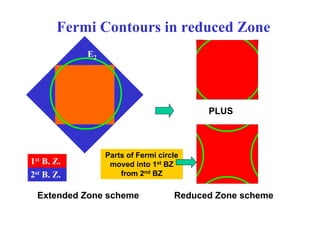
8. E = -α –γ( Cos[kx x] - Cos[ky y]),
2D simple square
Lattice tight binding
Lattice tight binding
model.
Changing Fermi
Changing Fermi
Contour with
I i F i
Increasing Fermi
Energy.
http://dept.physics.upenn.edu/~mele/phys518/anims/Kronig/FermiSurf1.gif

9. BZs and Fermi Surfaces with gaps
E2
E1
E2
/ /
E1
Energy gaps make the Fermi contours
0
−π/a −π/a
kx
1st B Z Energy gaps make the Fermi contours
appear discontinuous at the BZ boundaries.
dE/dk = 0 at BZ boundaries. Fermi contour
2st B. Z.
1st B. Z.
perpendicular to BZ boundary.

10. BZs and Fermi Surfaces with gaps
E
ky
No gaps With gaps
E2
E1
E1
E2
E1
1st B Z
2st B. Z.
1st B. Z.
Energy gaps: Fermi contours appear discontinuous at the BZ boundaries.
dE/dk = 0 at BZ boundaries. Fermi contour perpendicular to BZ boundary.

11. Fermi Surfaces with gaps “Hole
Fermi Surfaces with gaps “Hole
like” orbits
like orbits
Periodic zone picture of
part of the Fermi contour
at energy E1.
1
On this part of the Fermi
contour electrons behave
lik iti l h d
like positively charged
“holes”. See later

12. Fermi Surfaces with gaps:
Fermi Surfaces with gaps:
“Electron like” orbits
Periodic zone picture of
Periodic zone picture of
part of the Fermi contour
at energy E2.
On this part of the Fermi
contour electrons behave
like negatively charged
like negatively charged
“electrons”. See later

13. Motion in a magnetic field
Motion in a magnetic field
Free electrons B
k
B
v
F ×
−
=
×
−
= )
/
( m
e
e =
The electrons move in circles in real space and in k-space.
Bloch electrons B
k
B
v
k
k ×
∇
−
=
×
−
= )
(
2
E
e
e
dt
d
=
=
In both cases the Lorentz force does not change the energy of the
electrons. The electrons move on contours of constant E.
y k
y ky
x kx

14. Electron and Hole orbits
dk
dk
dk
dk
B
)
k
(
E
e
dt
k
d
k
2
×
∇
−
=
=
Filled states are indicated in grey.
dE
dk
dk
dE
dt
dE
dk
dk
dE
dt
dE
dk dE
dk
dk
dE
dt
dk
dE
dt
dk
dt
dk
Bz
ky
ky dk
dt
dk
dk
dt dk
dt
dk
dk
Bz
Bz
ky
ky
(a) (b)
(a) (b)
kx
kx kx
kx
(a) Electron like orbit centred on k = 0. Electrons move anti-clockwise.
(b) Hole like orbit. Electrons move clockwise as if they have positive
charge

15. Electron like orbits
Periodic zone
picture of Fermi
contour ( E ) near
contour ( E1 ) near
bottom of a band.
E1
Grad E
E
k /
/ 0
E1
kx π/a
−π/a 0

16. Hole like
orbits
Periodic zone
picture of the
Fermi contour at
Fermi contour at
the top of a band
Grad E
Grad E
E
E2
E
E2
k /
π/a 0 kx π/a
−π/a 0

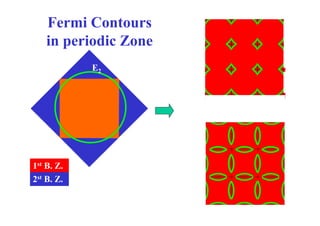
17. Tight binding simple cubic
d l F i S f
model:Fermi Surfaces
-α – γ(Cos[kx x] - Cos[ky y] - Cos[kz z]
Increasing Fermi Energy
h //h i b / l l /f i i l h l
http://home.cc.umanitoba.ca/~loly/fermiarticle.html

18. The Fermi Metals have a Fermi energy E
Surface
Metals have a Fermi energy, EF.
The Fermi Temperature,TF, is the
temperature at which kBTF = EF
temperature at which kBTF = EF.
All the free electron states within
a Fermi sphere in k-space are
a Fermi sphere in k space are
filled up to a Fermi wavevector,kF.
The surface of this sphere is
The surface of this sphere is
called the Fermi surface.
On the Fermi surface the free
electrons have a Fermi velocity vF
= hkF/me.
A Fermi surface still exists when the states are not free
A Fermi surface still exists when the states are not free
electron states but it need not be a sphere.

19. Sodium Copper
http://www.phys.ufl.e
d /f i f /h
du/fermisurface/http
Strontium

20. Lead

21. Palladium

22. Tungsten
g

23. Yttrium
Y

24. Thorium
Thorium

25. Rhenium
Re