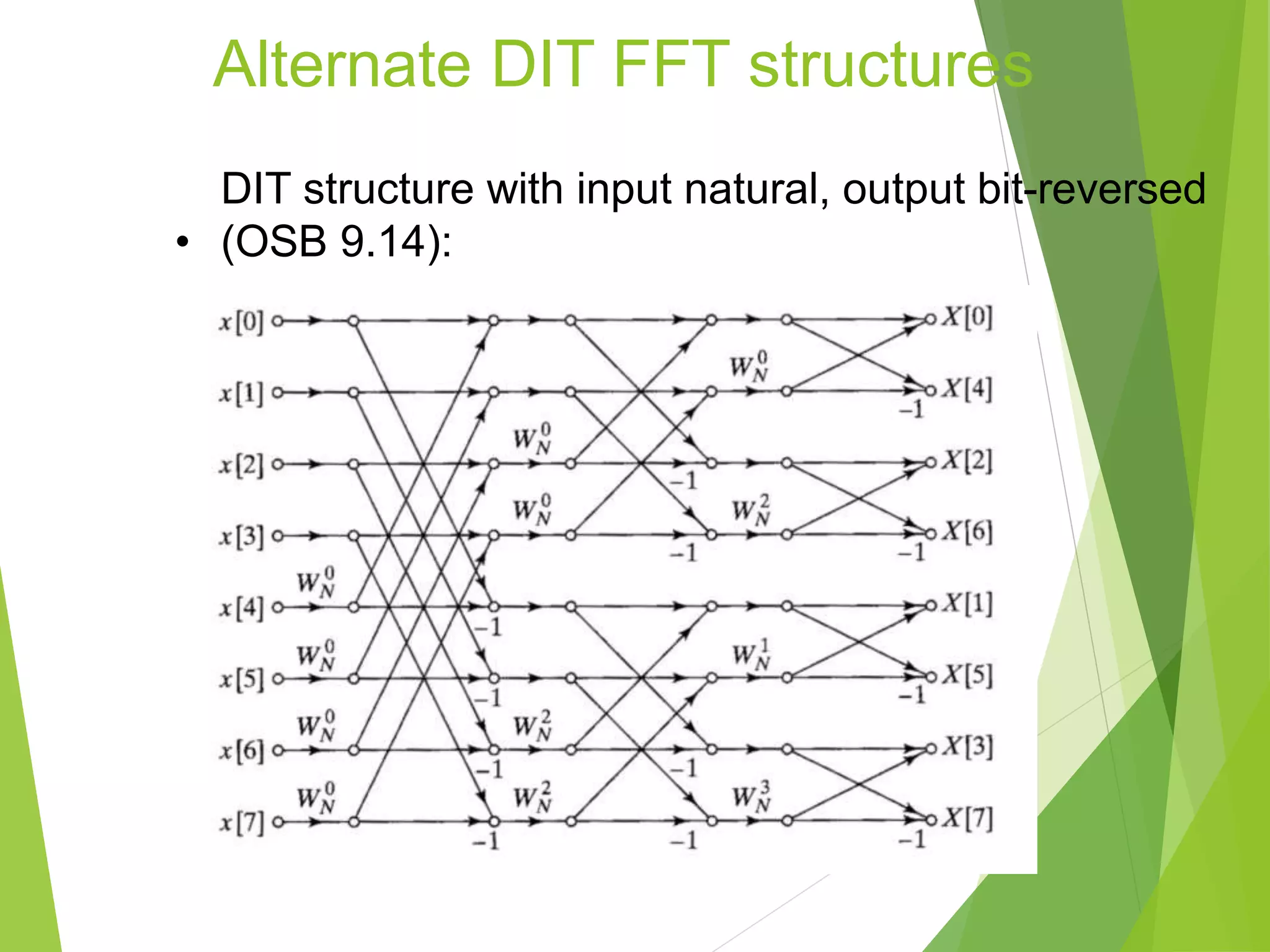
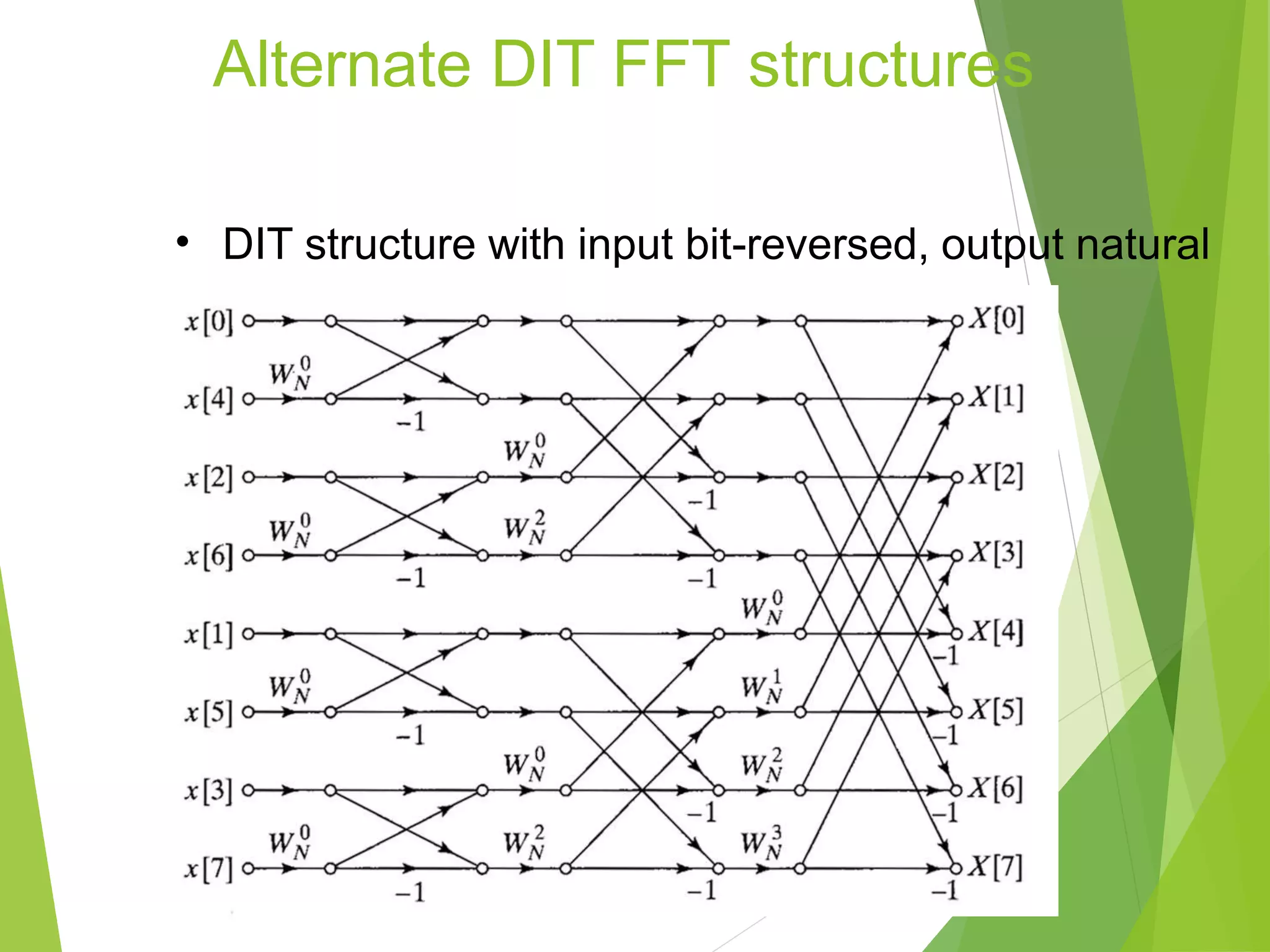
The document discusses fast Fourier transforms (FFTs), which are efficient algorithms for computing the discrete Fourier transform (DFT) and its inverse. FFTs require fewer arithmetic operations than directly computing the DFT, making them faster. There are different FFT algorithms that exploit properties of symmetry and periodicity to improve efficiency compared to direct computation of the DFT. The document provides an example of using a radix-2 decimation-in-frequency FFT algorithm to compute the DFT of a given discrete-time sequence.

1. Maharashtra Institute of Technology, Aurangabad
Electrical Engineering
FAST FORIER TRANSFORM (FFT)
Presented by:
Sumedh A. Bhagat [EE1180]

2. Fast Fourier Transform FFT
 A fast Fourier transform (FFT) is an efficient
algorithm to compute the discrete Fourier
transform (DFT) and inverse of DFT.
 There are many FFT algorithms which
involves a wide range of mathematics,. A
Discrete Fourier transform decomposes a
sequence of values into components of
different frequencies.
 This operation is very useful in many
fields but computing it directly from
the definition is often too slow to be
practical .

3. Cont ..
• FFT are special algorithms for speedier implementation of DFT.
• FFT requires a smaller number of arithmetic operations such
as multiplications and additions than DFT.
• FFT also requires lesser computational time than DFT .

4. Fast Fourier Transform Algorithms
•
•
Direct computation of the DFT is less efficient because it does
not exploit the properties of symmetry and periodicity of the
phase factor WN = e–j2π/N.
These properties are:
- Symmetry property.
- Periodicity property.
• As we already know that all computationally efficient algorithms
for DFT are collectively known as FFT Algorithms and these
algorithms exploit the above two properties of phase factor, WN.

5. Alternate DIT FFT structures
•
DIT structure with input natural, output bit-reversed
(OSB 9.14):

6. Alternate DIT FFT structures
• DIT structure with input bit-reversed, output natural

7. •
•
Example Find the DFT of the following discrete-time
sequence .
s(n) = {1, -1, -1, -1, 1, 1, 1, -1}
using
Radix-2 decimation-in-frequency FFT algorithm.
• Solution. The Twiddle factor or phase rotation factor
WN= involved in the FFT calculation are found out as
follows for N= 8.

8. Example Part1

9. Example Part1