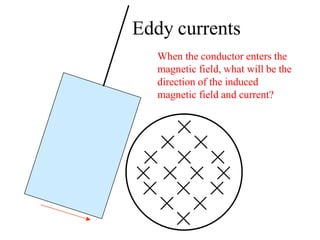
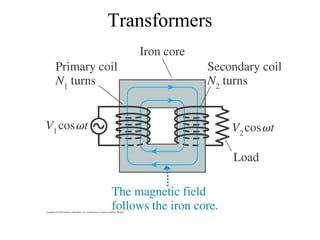
Michael Faraday was a British physicist and chemist in the 19th century who made many contributions to the field of electromagnetism. Some of his most important discoveries include the principles of electromagnetic induction, which established that a changing magnetic field can generate an electric current. He invented the electric motor, generator, and transformer based on these principles. Faraday established the laws of electrolysis through his experiments with electrolysis.

1. Michael Faraday
• 1791 – 1867
• British physicist and chemist
• Great experimental scientist
• Contributions to early
electricity include:
– Invention of motor,
generator, and transformer
– Electromagnetic induction
– Laws of electrolysis

2. Generator Effect: EM Induction
A changing magnetic flux induces an EMF.
Magnet moves in a stationary coil.
+
-

3. EM Induction
The magnet is pushed into the coil.
What is the direction of the induced current?
+
-
B

4. Michael
Faraday
(1791 - 1867)
d
dt
 = -
N
Faraday’s Law of Induction

5. induced
dt
 N
dext

number of
loops
Emf that drives the
induced current
(nonconservative)
Faraday’s Law
How quickly you change
the number of external field
lines through one loop.
Opposes the change
in magnetic flux
Lenz’s law: the induced current in a
loop is in the direction that creates a
magnetic field that opposes the change
in magnetic flux through the area
enclosed by the loop

6. FLUX Magnetic FLUX
d  B dA
d  BcosdA
The amount of FLOW
perpendicular to a surface!
  B dA
The flux depends on the
magnitude of the B field, the area,
A, it intersects and the angle
between them. Changes in B, A
or θproduce a change in the
magnetic flux.

7. Magnetic Flux
Maximum
Flux
 = 0
Maximum
Flux
 = 180
Minimum
Flux
 = 90
Magnetic Flux: B  BAcos
B

8. Maxwell’s Equations
Gauss's law electric:

Faraday's law:
Ampere-Maxwell law
S
S
εo
EdA 
q
Gauss's law in (magnetic): BdA  0
E
d
dt
Eds  
dB
Bds  μo I μo
dt

9. d
dt
 = -
N
Faraday’s Law of Induction
dt dt open

closed
  Eds  
dB
 
d
 BdA
The emf induced in a closed loop is directly proportional to the
time rate of change of the magnetic flux through the loop. The
electric field is path dependent – E is NOT conservative.

10. Why does the Ring Jump?
Lenz’s Law!

11. Great Demo: Jumping Ring
The magnetic force on each bit of ring is radially inward and upward, at
angle  above the radial line. The radially inward components tend to
squeeze the ring but all cancel out as forces. The upward components add:
F  ILB  dF  IdsBsin  F  IBsin ds
F  I2 rBsin up

12. EM Induction
The induced EMF produces a a current that produces a magnetic field
that opposes the original changing magnetic field.
To find the direction of the induced current:
1. Determine the flux change: Increasing? Decreasing?
2. The induced B field will be opposite. Find that.
3. Find the current with the RHR to produce the induced B field.

13. A conducting loop is
halfway into a magnetic
field. Suppose the magnetic
field begins to increase
rapidly in strength. What
happens to the loop?
1. The loop is pushed upward, toward the top of the page.
2. The loop is pushed downward, toward the bottom of the page.
3. The loop is pulled to the left, into the magnetic field.
4. The loop is pushed to the right, out of the magnetic field.
5. The tension is the wires increases but the loop does not move.

14. A conducting loop is
halfway into a magnetic
field. Suppose the magnetic
field begins to increase
rapidly in strength. What
happens to the loop?
1. The loop is pushed upward, toward the top of the page.
2. The loop is pushed downward, toward the bottom of the page.
3. The loop is pulled to the left, into the magnetic field.
4. The loop is pushed to the right, out of the magnetic field.
5. The tension is the wires increases but the loop does not move.

15. Faraday’s Law of Induction
The emf induced in a closed loop is directly
proportional to the time rate of change of the
magnetic flux through the loop.
open
dt

closed
  Eds  
dB
   BdA
How many ways can the flux change?
dt
 =-N
d =-N
d(ABcos)
dt

16. Sound Reproduction: B Changes
 =-N
d
=-N
d(ABcos)
dt dt

17. Angle Changes: Generators
 =-N
d
=-N
d(ABcos)
dt dt

18.  =-N
d
=-N
d(ABcos)
dt dt
Area Changes: Motional EMF

19. The Hall Effect
When a current carrying conductor is placed in a magnetic field, the
magnetic force causes a separation of charge in the conductor which
produces a charge separation and voltage, VH, in a direction that is
perpendicular to both the current and the magnetic field.
This Hall voltage produces an E field that opposes the Hall
Effect and tries to push the electrons back up. Eventually,
balance is reached. By measuring the voltage you can use a
hall probe to measure the magnetic field.
VH  qE  qvd B

20. • A motional emf is the emf
induced in a conductor
moving through a constant
magnetic field. The Hall
Effect induces an emf.
• The electrons in the
conductor experience a
force,
that is directed along ℓ
• The charges accumulate at
both ends of the conductor
until they are in equilibrium
with regard to the electric
and magnetic forces.
F  qvB
F  qvB  qE  q(l )
E  vB
 = Blv

21. Forces on a Sliding Conducting Bar
• The applied force to the right must balance the
magnetic force to keep the bar moving at constant
speed. The force does work on the bar.
• The magnetic force on the induced current in the
wire is opposite the motion of the bar.
Fapp  FB
B
F  I B 

( ) B  (
vLB
) B
R R
v 2
B2
R
Fapp  FB 

22. Sliding Conducting Bar Circuit
I 
ε

B v
R R
• A bar moving through a uniform field and the
equivalent circuit diagram
• Assume the bar has zero resistance and the stationary
part of the circuit has a resistance R
• The induced current obeys Ohms Law
 = Blv

23. εMotional Emf  = Blv
I 
ε

B v
R R
v 2
B2
R
Fapp  FB 

24. Geomagnetic Induction and Thrust
The forces generated by this
"electrodynamic" tether can be used to
pull or push a spacecraft to act as a brake
or a booster or to generate voltage.

25. Calculate the motional emf
induces alonga 20 km long
conductor moving at the
orbital speed of 7.8 km/s
perpendicular to the Earth’s
0.5 microT magnetic field.
 = Blv
Tethered Satellite Experiment

26. Cool Problem! Incline Generator!

27. Eddy Currents
Current loops in moving currents create drag
due to magnetic damping.

28. Eddy currents
When the conductor enters the
magnetic field, what will be the
direction of the induced
magnetic field and current?

29. Eddy currents
What will be the direction of
the magnetic force on the
current in the conductor?

30. Eddy currents
F
What will be the direction of
the magnetic force on the
current in the conductor?
The force
slows the
conductor.

31. Eddy Currents
• To reduce energy loses by
the eddy currents, the
conducting parts can
– Be built up in thin layers
separated by a
nonconducting material
– Have slots cut in the
conducting plate
• Both prevent large current
loops and increase the
efficiency of the device

33.  =-N
(ABcos)
t
open
dt

closed
  Eds  
dB
   BdA
Area of Coil Changes

34. Eddy Currents & National
Security!!

35. Traffic Light Triggering
A traffic light sensor uses an inductance loop in the
road. When a car sits on top of the loop, the
inductance is changed due to eddy currents in the
steel in the car. The sensor constantly tests the
inductance of the loop in the road, and when the
inductance rises, it knows there is a car waiting!

36. Traffic Loops

37. AC Generators
dt dt
  NABsint
For a coil with N turns, area A, turning at angular
speed  the induced EMF is:
 = -N
d
 -N
d BAcos   -N
d BAcost
dt
(: rad/s)

38. Generator Problem
The 500 turn square coil has sides of
length 10.0 cm and is in a uniform 1.25 T
magnetic field. Initially the coil is
perpendicular to the field and then it is
turned 90 degrees as shown in 0.05s.
a) Does the magnetic flux through the coil
increase or decrease during the ¼ turn?
b) What is the average EMF induced?
c) At what time is the EMF maximum?
What is the maximum EMF?
d) What is the frequency of the ac
generated?

39. AC VS DC Generators
In an AC electric generator, or
alternator, the flux through the
loops of wire (wound on the
armature) changes, and therefore
according to Faraday's law there
will be an emf induced in the
loops of wire.
In a DC generator the direction
of the induced current in the
loops must be changed every
one-half turn of the generator
shaft. This is done with split
rings on the rotating armature
contacting the stationary
"brushes" which are in turn
connected to the wires coming
out of the generator.

40. Motors & Generators
Magnetic Force on
Moving Charges in
Loop: Motor Effect
Magnetic Field
Changing through
Loop: Generator Effect
Motor Effect Generator Effect

41. Sources of Electrical Power
Solar doesn’t use a EM induction!!

42. Power Production
Coal, Nuclear, Oil or Gas:
It all comes down to making
HOT WATER & STEAM
to turn a turbine!

43. Wind & Tidal Turbines

44. Transformers

45. PP  PS  ISVS  IPVP
VS

IP

NS
VP IS NP
Voltage and Current Change but Energy & Power DO NOT!
EM Inductance:Transformers
S
S P
P
V
N
N
V  S P
S
NP
N
I  I
o
B  μ
N
I  I 
1
N
Step UP
Step Down
NS  NP
NS  NP
“Step” refers to VOLTAGE:

46. Transformers
S
S P
NP
N
V  V
Step Down
Decrease Voltage
Increase Current
Step UP
Increase Voltage
Decrease Current
NP
S P
S
I  I
N

47. Transformers and Auto Ignition
Converting 12V to 40,000V

48. Power Transmission
Step up Voltage Step Down Current to reduce Power loss.
S
S P
NP
N
V  V
NP
S P
S
I  I
N
Transformers
(Modern transmission grids use AC voltages up to 765,000 volts.)

49. The Power Grid
Typical power plant can generate MegaWatts of Energy.
US consumption of electricity is 90 Quadrillion BTUs/year.
1 quad = 1015 Btu = 2.931 x 1011 kW-hrs
Hetch Hetchy: 2 billion kW-hrs per year
Wind in CA: 4.5 million kW-hrs per year

50. In The Future….
Long Distance AC Power Transmission
may not be needed!!!

51. Advantages of AC Transmission
• Alternating Current can be transformed to ‘step’ the voltage up or down
with transformers.
• Power is transmitted at great distances at HIGH voltages and LOW
currents and then stepped down to low voltages for use in homes (240V)
and industry (440V).
• Convert AC to DC with a rectifier in appliances.
AC is more efficient for
Transmission & Distribution of
electrical power than DC!

52. War of Currents 1880’s
Thomas Edison, American
inventor and businessman,
pushed for the development of
a DC power network.
George Westinghouse,
American entrepreneur
and engineer, backed
financially the
development of a
practical AC power
network.
Nikola Tesla, Serbian
inventor, physicist,
and electro-
mechanical engineer,
was instrumental in
developing AC
networks.