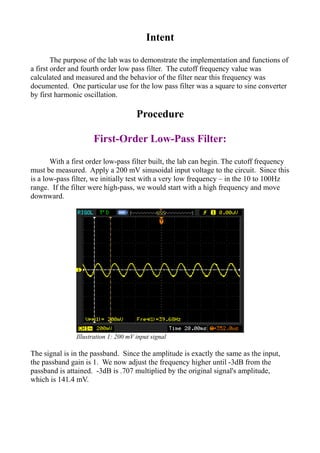
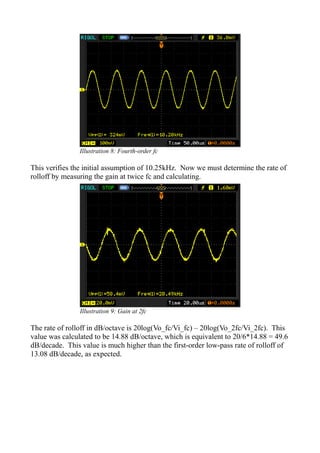
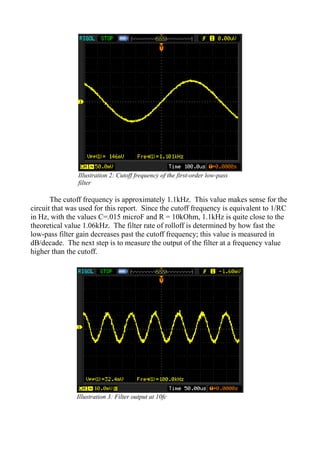
The document summarizes an experiment that tested and characterized first-order and fourth-order low pass filters. Key findings include: - The cutoff frequency was measured to be 1.1 kHz for the first-order filter and 10.2 kHz for the fourth-order filter, close to theoretical calculations. - The first-order filter had a rolloff rate of 13.08 dB/decade while the fourth-order was 49.6 dB/decade as expected for higher order filters. 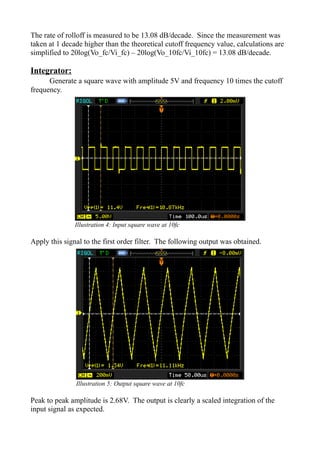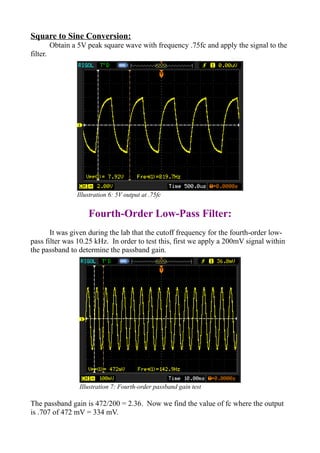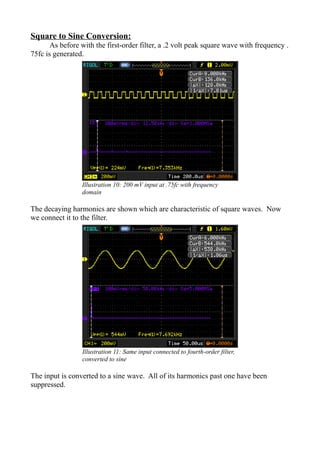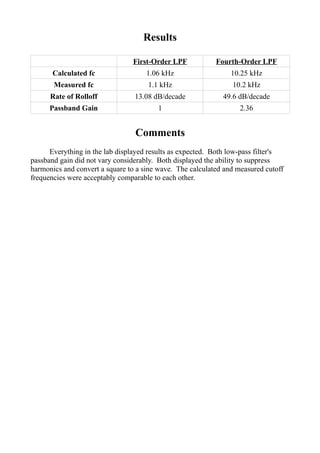- Both filters were able to suppress harmonics and convert a square wave input to a sine wave output as intended applications of low pass filters.

1. Katrina Little
Max Molesch
2/5/12
Experiment 3: Low Pass Filter

2. Intent
The purpose of the lab was to demonstrate the implementation and functions of
a first order and fourth order low pass filter. The cutoff frequency value was
calculated and measured and the behavior of the filter near this frequency was
documented. One particular use for the low pass filter was a square to sine converter
by first harmonic oscillation.
Procedure
First-Order Low-Pass Filter:
With a first order low-pass filter built, the lab can begin. The cutoff frequency
must be measured. Apply a 200 mV sinusoidal input voltage to the circuit. Since this
is a low-pass filter, we initially test with a very low frequency – in the 10 to 100Hz
range. If the filter were high-pass, we would start with a high frequency and move
downward.
The signal is in the passband. Since the amplitude is exactly the same as the input,
the passband gain is 1. We now adjust the frequency higher until -3dB from the
passband is attained. -3dB is .707 multiplied by the original signal's amplitude,
which is 141.4 mV.
Illustration 1: 200 mV input signal

3. The cutoff frequency is approximately 1.1kHz. This value makes sense for the
circuit that was used for this report. Since the cutoff frequency is equivalent to 1/RC
in Hz, with the values C=.015 microF and R = 10kOhm, 1.1kHz is quite close to the
theoretical value 1.06kHz. The filter rate of rolloff is determined by how fast the
low-pass filter gain decreases past the cutoff frequency; this value is measured in
dB/decade. The next step is to measure the output of the filter at a frequency value
higher than the cutoff.
Illustration 2: Cutoff frequency of the first-order low-pass
filter
Illustration 3: Filter output at 10fc

4. The rate of rolloff is measured to be 13.08 dB/decade. Since the measurement was
taken at 1 decade higher than the theoretical cutoff frequency value, calculations are
simplified to 20log(Vo_fc/Vi_fc) – 20log(Vo_10fc/Vi_10fc) = 13.08 dB/decade.
Integrator:
Generate a square wave with amplitude 5V and frequency 10 times the cutoff
frequency.
Apply this signal to the first order filter. The following output was obtained.
Peak to peak amplitude is 2.68V. The output is clearly a scaled integration of the
input signal as expected.
Illustration 4: Input square wave at 10fc
Illustration 5: Output square wave at 10fc

5. Square to Sine Conversion:
Obtain a 5V peak square wave with frequency .75fc and apply the signal to the
filter.
Fourth-Order Low-Pass Filter:
It was given during the lab that the cutoff frequency for the fourth-order low-
pass filter was 10.25 kHz. In order to test this, first we apply a 200mV signal within
the passband to determine the passband gain.
The passband gain is 472/200 = 2.36. Now we find the value of fc where the output
is .707 of 472 mV = 334 mV.
Illustration 6: 5V output at .75fc
Illustration 7: Fourth-order passband gain test

6. This verifies the initial assumption of 10.25kHz. Now we must determine the rate of
rolloff by measuring the gain at twice fc and calculating.
The rate of rolloff in dB/octave is 20log(Vo_fc/Vi_fc) – 20log(Vo_2fc/Vi_2fc). This
value was calculated to be 14.88 dB/octave, which is equivalent to 20/6*14.88 = 49.6
dB/decade. This value is much higher than the first-order low-pass rate of rolloff of
13.08 dB/decade, as expected.
Illustration 8: Fourth-order fc
Illustration 9: Gain at 2fc

7. Square to Sine Conversion:
As before with the first-order filter, a .2 volt peak square wave with frequency .
75fc is generated.
The decaying harmonics are shown which are characteristic of square waves. Now
we connect it to the filter.
The input is converted to a sine wave. All of its harmonics past one have been
suppressed.
Illustration 10: 200 mV input at .75fc with frequency
domain
Illustration 11: Same input connected to fourth-order filter,
converted to sine

8. Results
First-Order LPF Fourth-Order LPF
Calculated fc 1.06 kHz 10.25 kHz
Measured fc 1.1 kHz 10.2 kHz
Rate of Rolloff 13.08 dB/decade 49.6 dB/decade
Passband Gain 1 2.36
Comments
Everything in the lab displayed results as expected. Both low-pass filter's
passband gain did not vary considerably. Both displayed the ability to suppress
harmonics and convert a square to a sine wave. The calculated and measured cutoff
frequencies were acceptably comparable to each other.