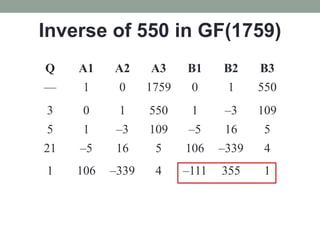
This document provides an overview of topics related to cryptography and network security including the Euclid algorithm, matrices, determinants, congruent matrices, and linear congruences. It discusses how matrices are useful for storing values, solving systems of equations, and transforming coordinates. It also explains how to use the Euclid and extended Euclid algorithms to find the greatest common divisor and modular inverses. Finally, it defines congruent matrices as two square matrices that are related by an invertible change of basis matrix, and how linear congruences are used to solve sets of linear equations.

1. CS8792 – CRYPTOGRAPHY AND
NETWORK SECURITY
UNIT 2 – EUCLID ALGORITHM AND
CONGRUENT MATRIX
~ S. Janani, AP/CSE
KCET

2. Contents
• Euclid algorithm
• Matrix - Definition
• Operations and relations
• Determinants
• Residue Matrix
• Congruent Matrix

3. Prerequisites
• GCD & Relative prime
• Why Matrix
• Congruent
• Congruent function – applications
• Inverse of a matrix

4. GCD & Relative prime

5. Why Matrix
• Matrices are very useful in engineering calculations.
• For example, matrices are used to:
– Efficiently store a large number of values (as we
have done with arrays in MATLAB)
– Solve systems of linear simultaneous equations
– Transform quantities from one coordinate system
to another

6. Congruent

7. Congruent Application
• To find whether the given number is odd or even
• To find the day of the particular date

8. Inverse of a matrix
• https://www.khanacademy.org/math/algebra-home/alg-
matrices/alg-determinants-and-inverses-of-large-
matrices/v/inverting-3x3-part-1-calculating-matrix-of-
minors-and-cofactor-matrix

9. Euclid Algorithm
• To find gcd of two integers
• gcd (a,b) = gcd(b,a mod b)

10. Extended Euclidean Algorithm
 calculates not only GCD but x & y:
ax + by = d = gcd(a, b)
 useful for later crypto computations
 follow sequence of divisions for GCD but
assume at each step i, can find x &y:
r = ax + by
 at end find GCD value and also x & y
 if GCD(a,b)=1 these values are inverses

11. Finding Inverses
EXTENDED EUCLID(m, b)
1. (A1, A2, A3)=(1, 0, m);
(B1, B2, B3)=(0, 1, b)
2. if B3 = 0
return A3 = gcd(m, b); no inverse
3. if B3 = 1
return B3 = gcd(m, b); B2 = b–1 mod m
4. Q = A3 div B3
5. (T1, T2, T3)=(A1 – Q B1, A2 – Q B2, A3 – Q B3)
6. (A1, A2, A3)=(B1, B2, B3)
7. (B1, B2, B3)=(T1, T2, T3)
8. goto 2

12. Inverse of 550 in GF(1759)
Q A1 A2 A3 B1 B2 B3
— 1 0 1759 0 1 550
3 0 1 550 1 –3 109
5 1 –3 109 –5 16 5
21 –5 16 5 106 –339 4
1 106 –339 4 –111 355 1
355 is inverse of 550

13. Matrix - Definition

14. Operations and Relations

15. Matrix Multiplication

16. Scalar Multiplication

17. Determinant of a Matrix

18. Residue Matrix

19. Congruent Matrix
• In mathematics, two square
matrices A and B over a field are
called congruent if there exists
an invertible matrix (Inverse Matrix) P over
the same field such that
• PTAP = B

20. Linear Congruence

21. Single variable linear equation

24. Set of Linear Equations