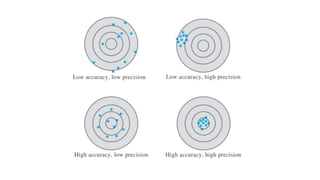
Errors refer to the differences between measured and true values in measurements and experiments. It is impossible to perform analyses that are completely free of errors. Errors are caused by faulty instruments, imprecise measurements, and random variations. Methods to reduce errors include frequent calibration of instruments, analysis of known samples, and repeating measurements. Precision refers to the reproducibility of measurements and can be estimated through repeated measurements of replicate samples. Accuracy is the closeness of a measurement to the true value and is more difficult to determine than precision. There are two main types of errors: determinate errors caused by mistakes that can be avoided, and accidental errors that are difficult to control. Methods to minimize errors include calibration, using blanks, comparative analysis techniques, and repeated

1. ERROR
The term error can be-
a. error refers to the difference between a measured value and the “true” or
“known” value.
b. error often denotes the estimated uncertainty in a measurement or
experiment.
 We should try to reduce errors and estimate their size with acceptable accuracy.

2. Measurements involve errors and uncertainties.
It is quite impossible to perform a chemical analysis that is totally free of
errors.
We should try to decrease errors and estimate their size with acceptable
accuracy
Errors are caused by faulty calibrations or standardizations or by random
variations and uncertainties in results.
Frequent calibrations, standardizations, and analysis of known samples can
sometimes be used for reducing random errors and uncertainties.

3. • Absolute error of a measurement is the difference between the measured value and the true
value. If the measurement result is low, the sign is negative; if the measurement result is high, the
sign is positive.
• Relative Error The relative error of a measurement is the absolute error divided by the true value.
Relative error may be expressed in percent, parts per thousand, or parts per million, depending
on the magnitude of the result.

4. Precision
o Precision is the reproducibility of measurements.
o Precision can be estimated by repeating the measurement on replicate samples.
o Precision of a set of replicate data may be expressed as standard deviation,
variance, and coefficient of variation.
o di , deviation from mean, is how much xi, the individual result, deviates from the
mean.
di= xi-x

5. The measure of precision is called the average deviation or coefficient of variation (KV). The formula for
calculating accuracy:
S: Standard deviation
X: The value of each observation
x bar: The average value of each observation
N: Number of data / Number of observations
A method is said to have good accuracy if KV is less than 3%.

6. Accuracy
Accuracy tells the closeness of the measurement to the true or exact value.
 Accuracy measures agreement between a result and the accepted value.
Accuracy is more difficult to determine in comparison to precision because the true value is
mostly unknown. An accepted value must be used instead.
Accuracy is can be absolute or relative error.

8. Types of Errors in
Quantitative Analysis
 There are 2 basic types of errors in quantitative analysis:
A)Error assigned (determinate error)
 Set errors are a mistake that can be avoided, the magnitude can be set, and occur repeatedly. The errors are
divided into 4 sections:
 Operational error
 Errors caused by humans are self-transcending and have nothing to do with experimental methods or procedures.
 Example:
 Non-quantitative treatment from analysts while experimenting.
 Heating at temperatures that are less precise.

9.  Error Instruments and Reagents
 Error analysts when using instruments or choosing reagents.
 Example:
 Instruments / tools used are not calibrated before use.
 The dirty burette is not cleaned before use
 The reagents used are not pure.
 Method Error
 Example:
 Incorrect sampling
 The reaction is not perfect.
 The presence of impurities on deposits when using Gravimetry.
 Selection of inappropriate indicators to determine the end point of the titration.

10.  Additive and Comparable Errors (Proportional)
 Proportional errors decrease or increase in proportion to the size of the sample. A common cause of proportional errors is
the presence of interfering contaminants in the sample.
 Example:
 The presence of impurities in the standard solution causes the increase in the quantity of constituents linearly or not, so that
it can result in an error of normality (N) value of a standard solution.
 Constant Errors
 The magnitude of a constant error stays essentially the same as the size of the quantity measured is varied. With constant
errors, the absolute error is constant with sample size, but the relative error varies when the sample size is changed. One way
of reducing the effect of constant error is to increase the sample size until the error is acceptable.
 Example:

11. B). Error not set (accidental error)
 Mistakes that occur even though the analyst has worked with the method of good and right with caution. For example,
there is little difference in repeated measurements. This is caused by causes that can not be controlled by the analyst and
generally difficult to understand.
 Personal Errors
 result from the carelessness, inattention, or personal limitations of the experimenter. Many measurements require personal
judgments.
 Examples include estimating the position of a pointer between two scale divisions; the colour of a solution at the end point
in a titration; or the level of a liquid with respect to a graduation in a pipet or burette. Judgments of this type are often
subject to systematic, unidirectional errors. Number bias is another source of personal error that varies considerably from
person to person. The most frequent number bias encountered in estimating the position of a needle on a scale involves a
preference for the digits 0 and 5. Also common is a prejudice favouring small digits over large and even numbers over odd.
Digital and computer displays on ph meters, laboratory balances, and other electronic instruments eliminate number bias
because no judgment is involved in taking a reading.

12. METHODS OF MINIMIZING ERRORS
 Calibrate tools and make corrections The instrument is calibrated and corrected against standard measurements in
order to determine whether the instrument used is in good condition (not damaged). In addition to calibration, it is
also important to wash glass-sized appliances (e.g. pipette) to clean and impurities free.
 Setting the blanks Make separate assignments to blanks. The objective is to know the presence of impurities in the
reagents and the correction of the standard solution to reach the end point of the titration. Correction value should not
be too big.
 Conducting surveillance Under identical conditions, determination is made of samples and standards containing
constituents of equal weight as contained in the sample.
 Using comparative analysis methods Analysis using different methods, e.g. determination of iron content (Fe) in the
sample by Gravimetry in comparison with the Volumetric method. The methods used are correct if the results obtained
do not differ significantly.

13. Perform a parallel assignment Check the results obtained from the analysis and make repeated
assignments. For example, titration is done 3 times not just once to get the right result. However, the
titration volume obtained should not differ much or more than 0.05.
Analysis of Standard Samples The overall composition of a synthetic standard material must closely
approximate the composition of the samples to be analysed. Great care must be taken to ensure that the
concentration of analyte is known exactly. A synthetic standard may not reveal unexpected interferences so
that the accuracy of determinations may not be known.
Most personal errors can be minimized by careful, disciplined laboratory work. It is a good habit to check
instrument readings, notebook entries, and calculations systematically.

14. THANK YOU!!