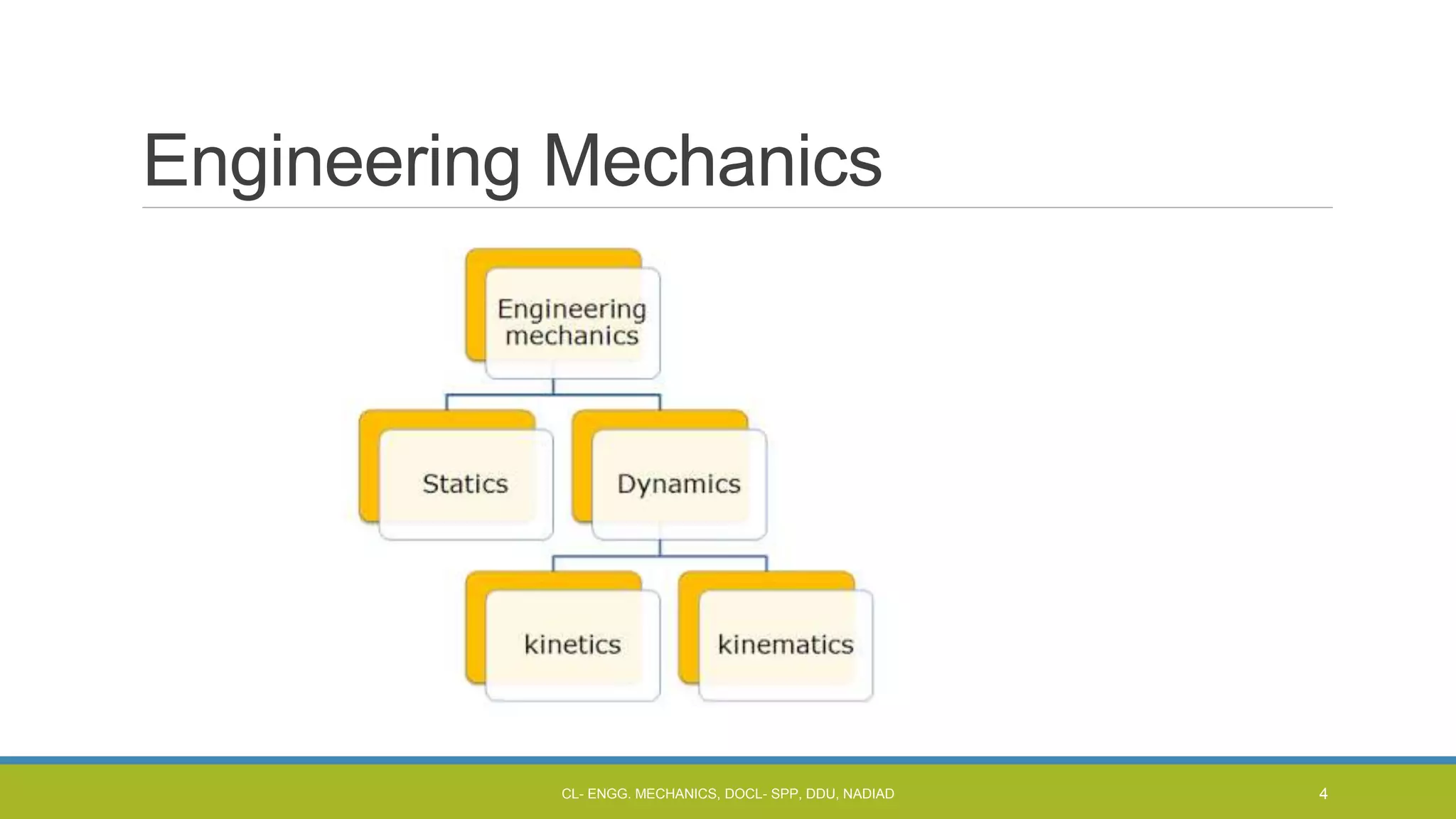
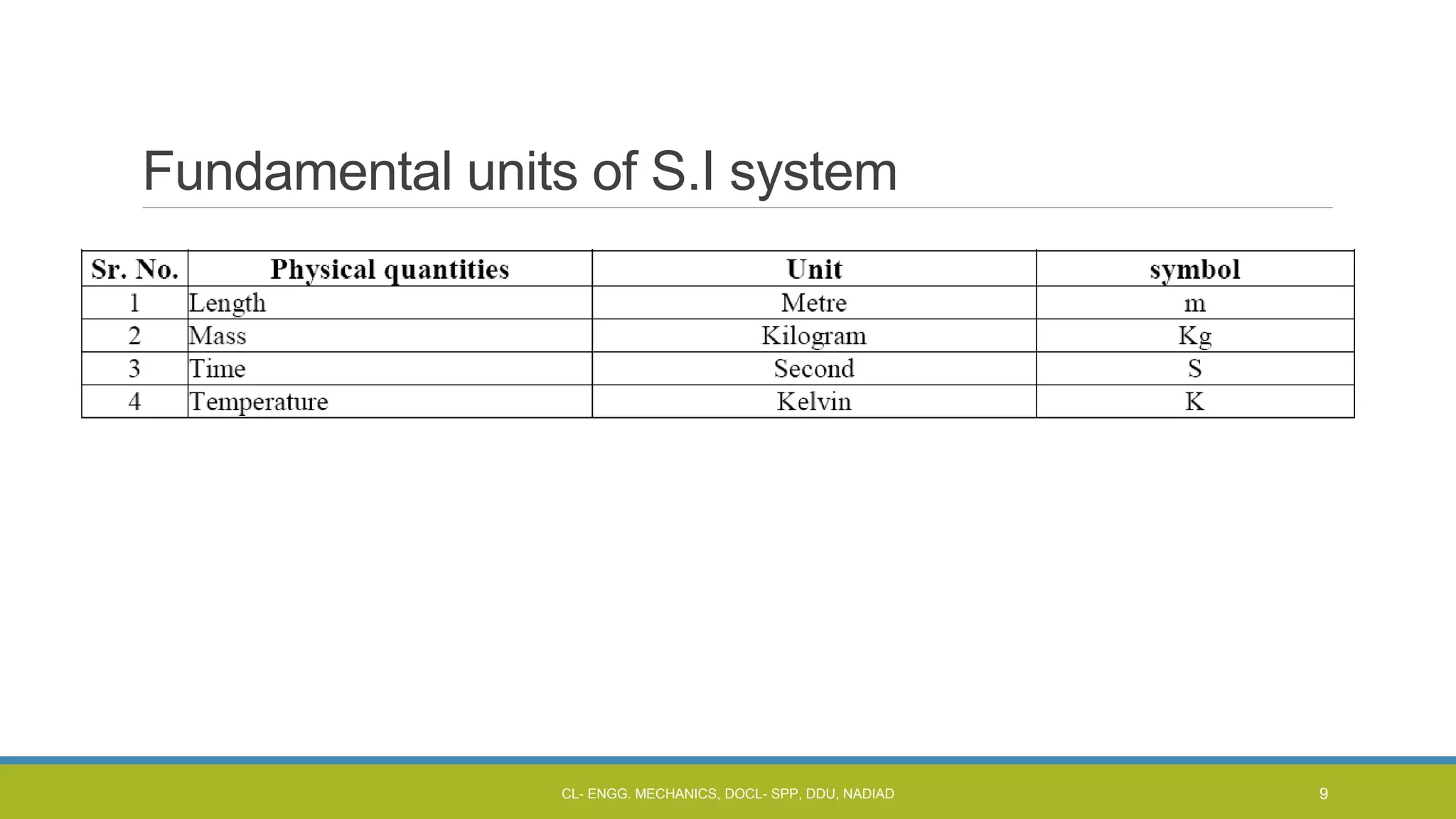
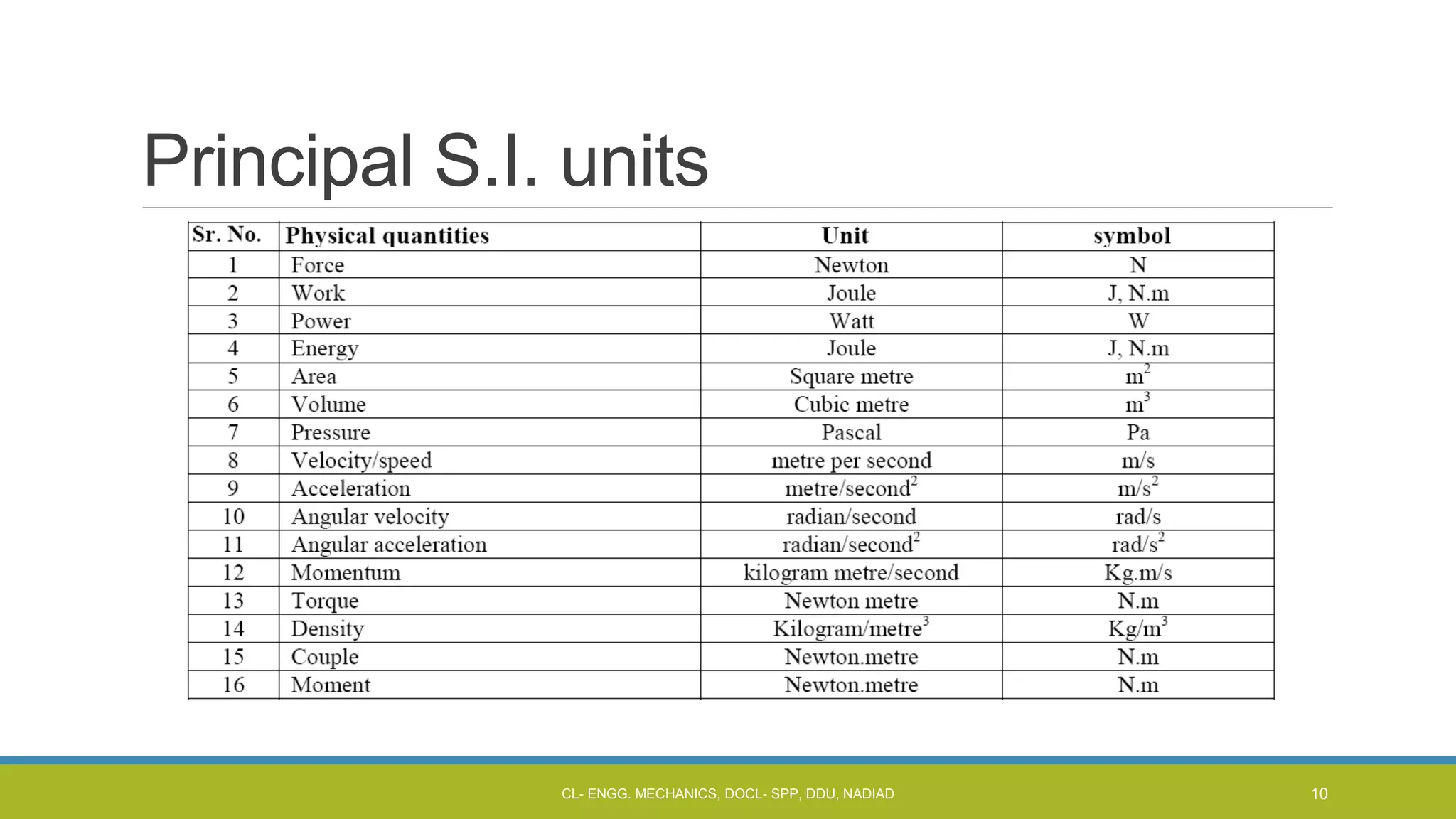
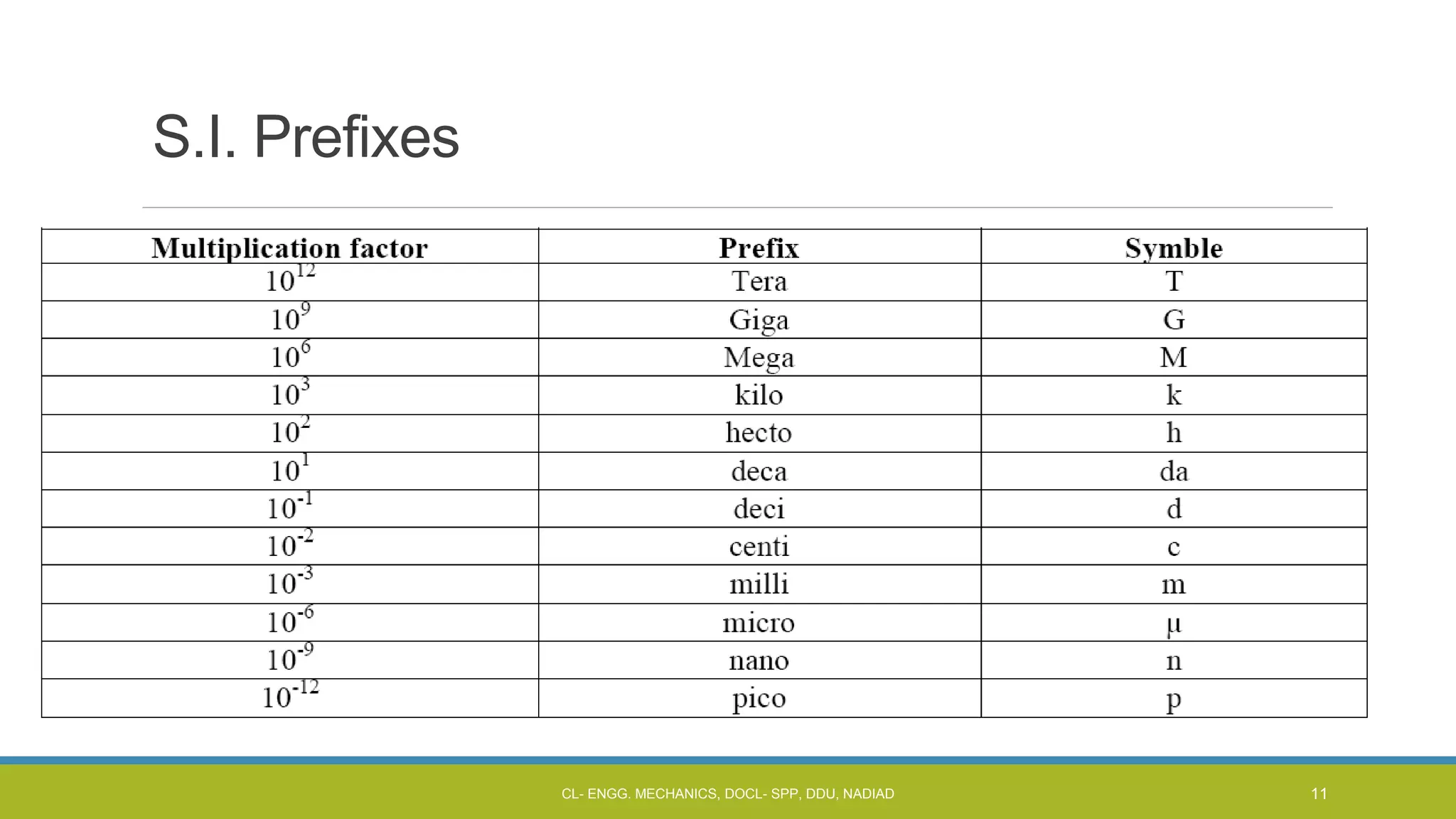
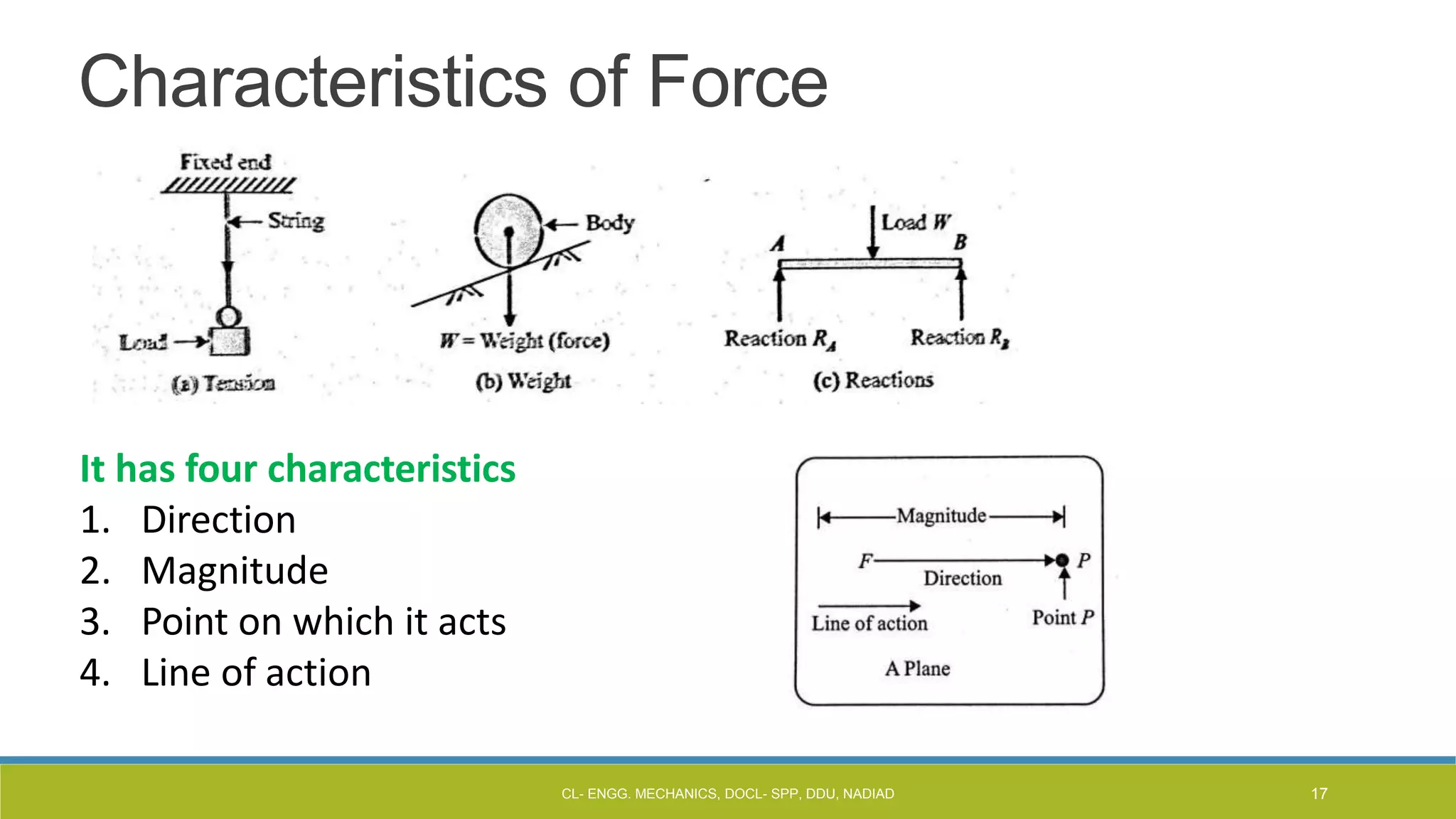
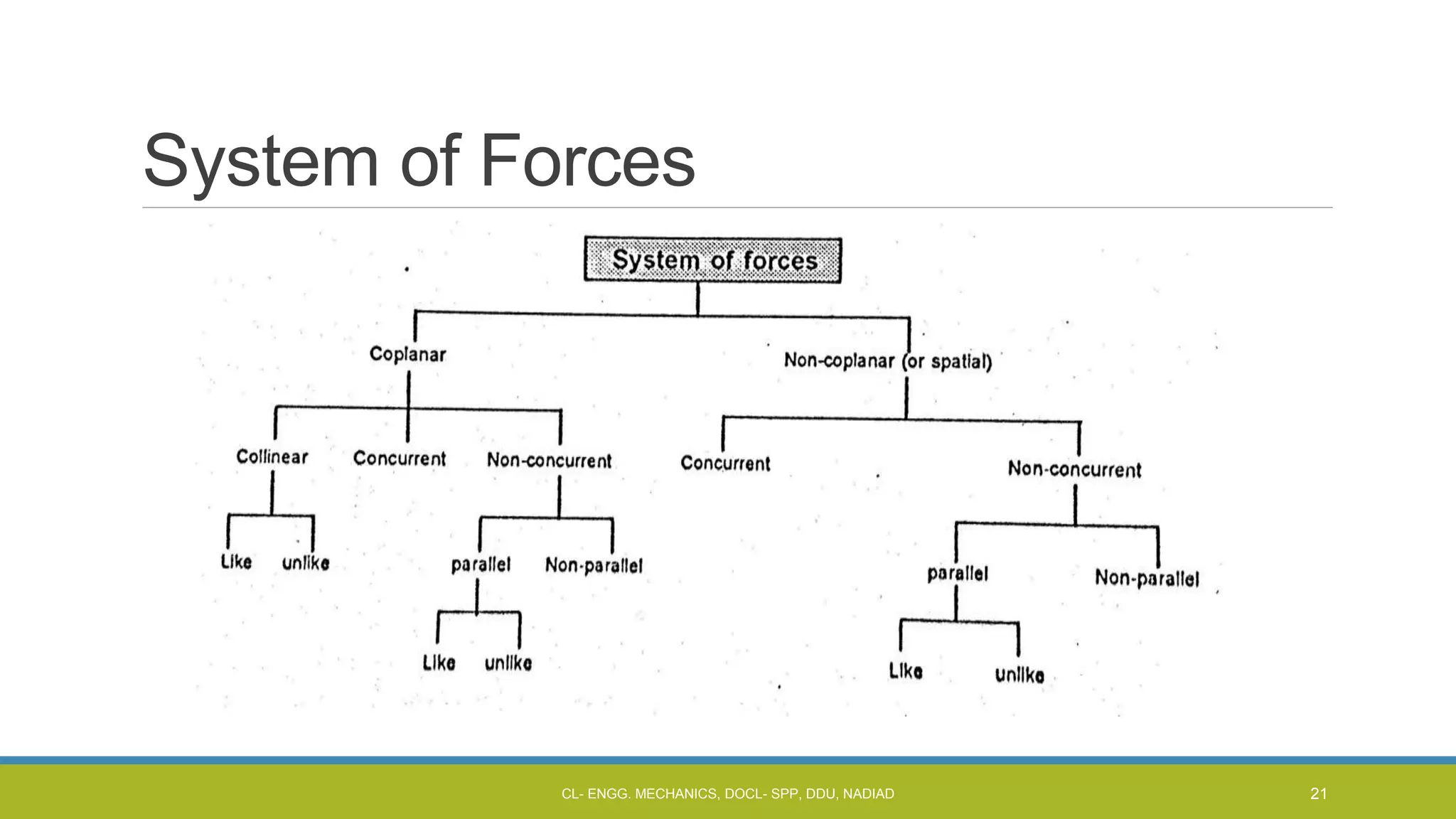
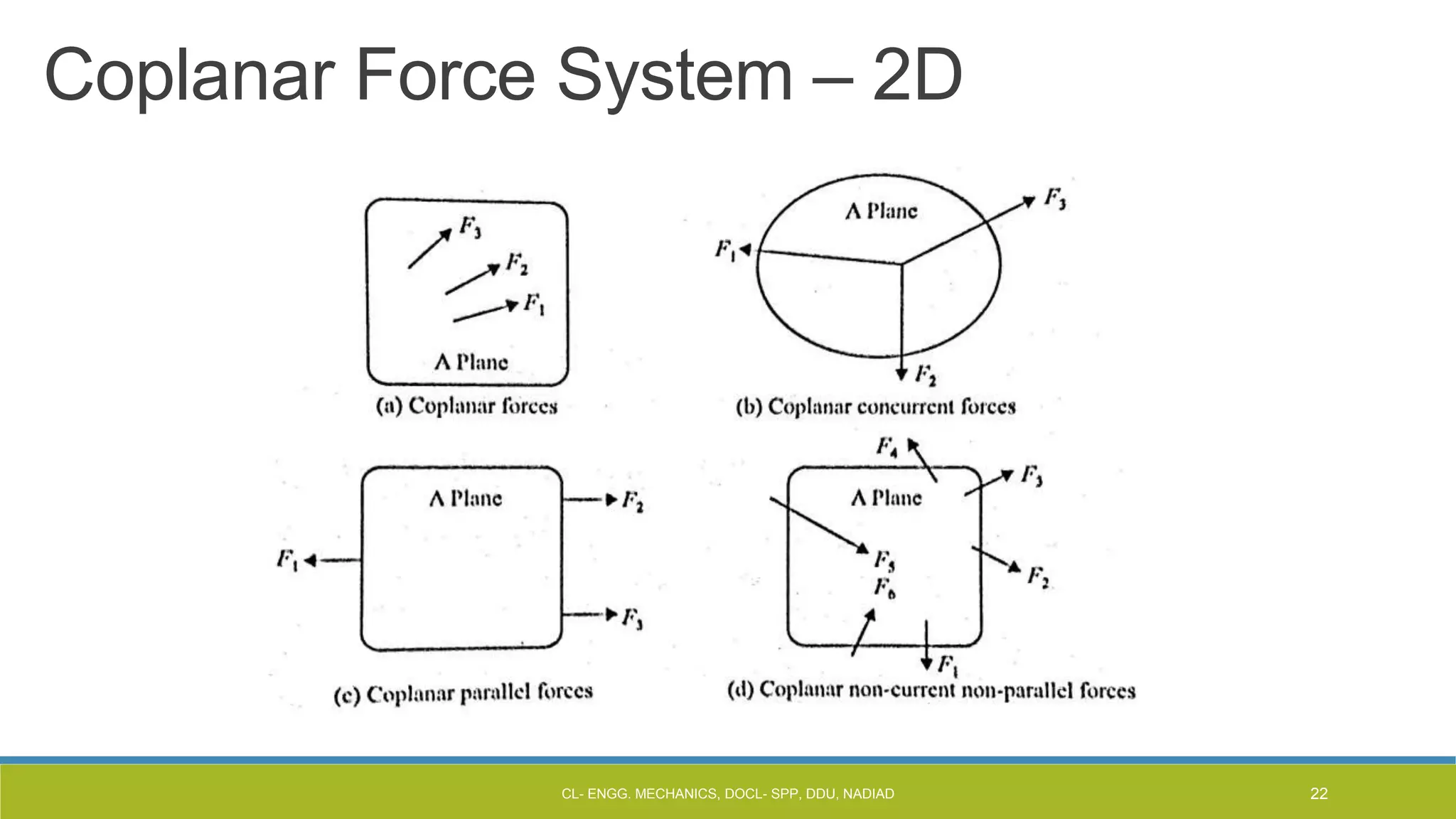
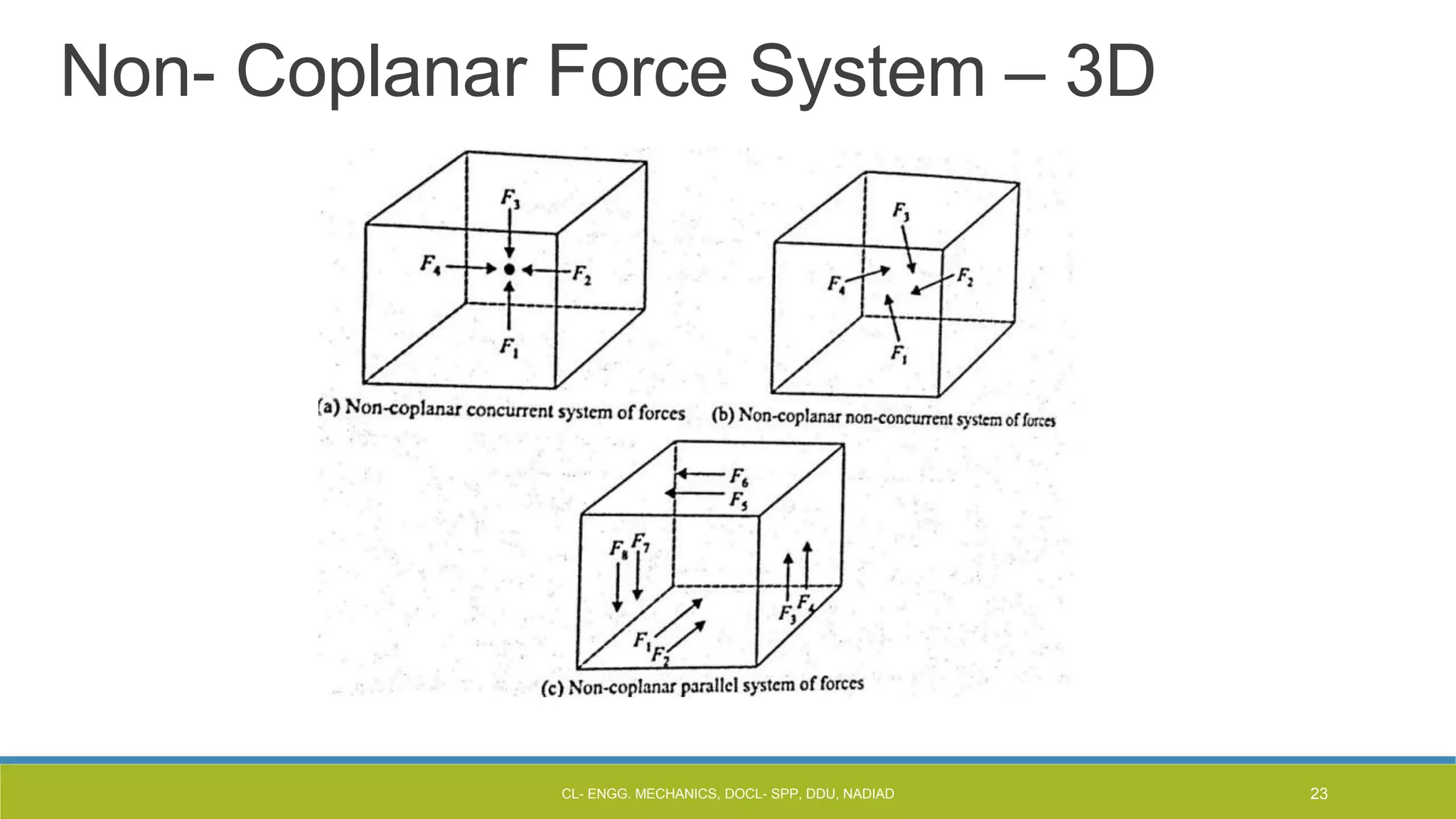
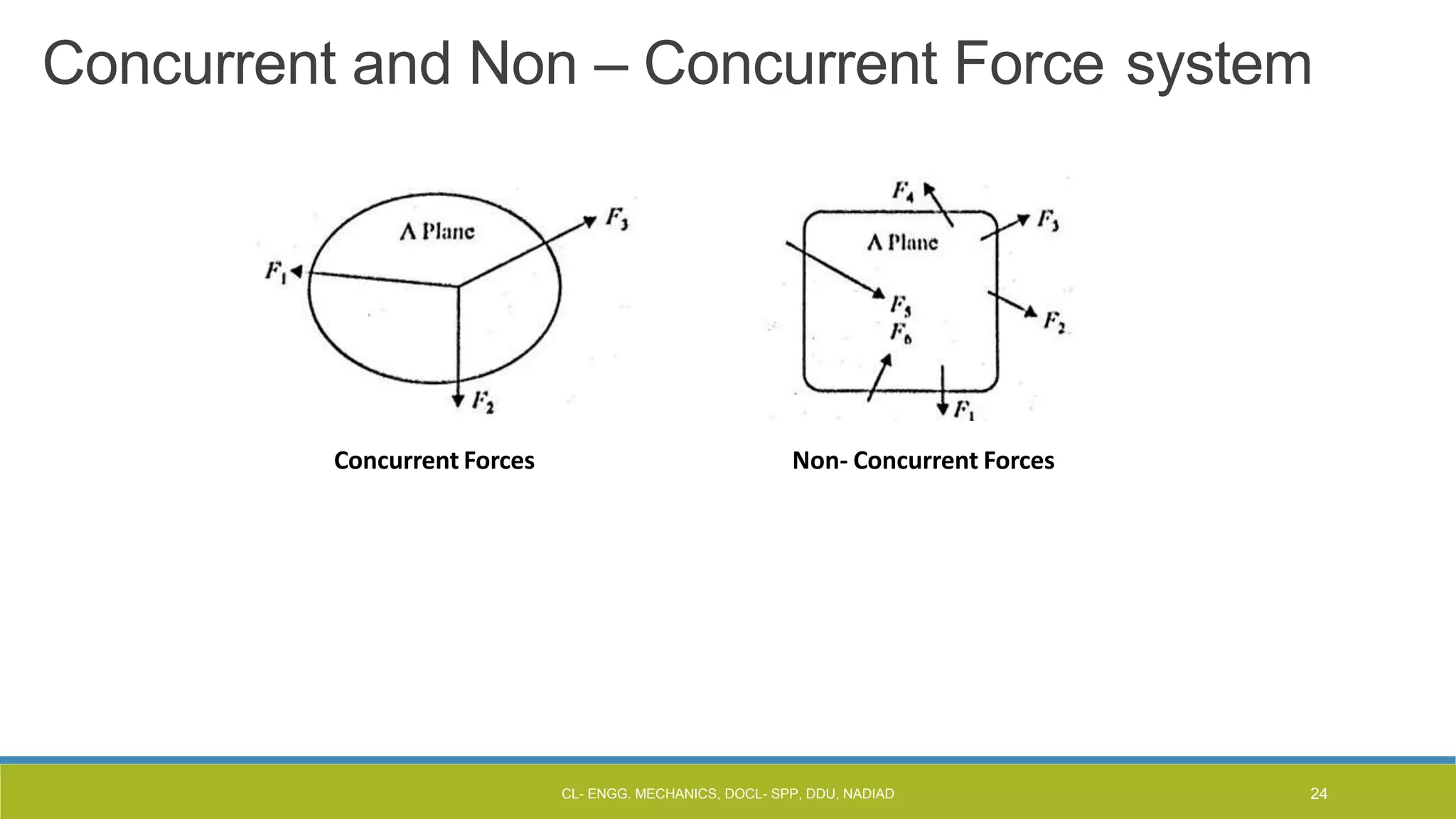
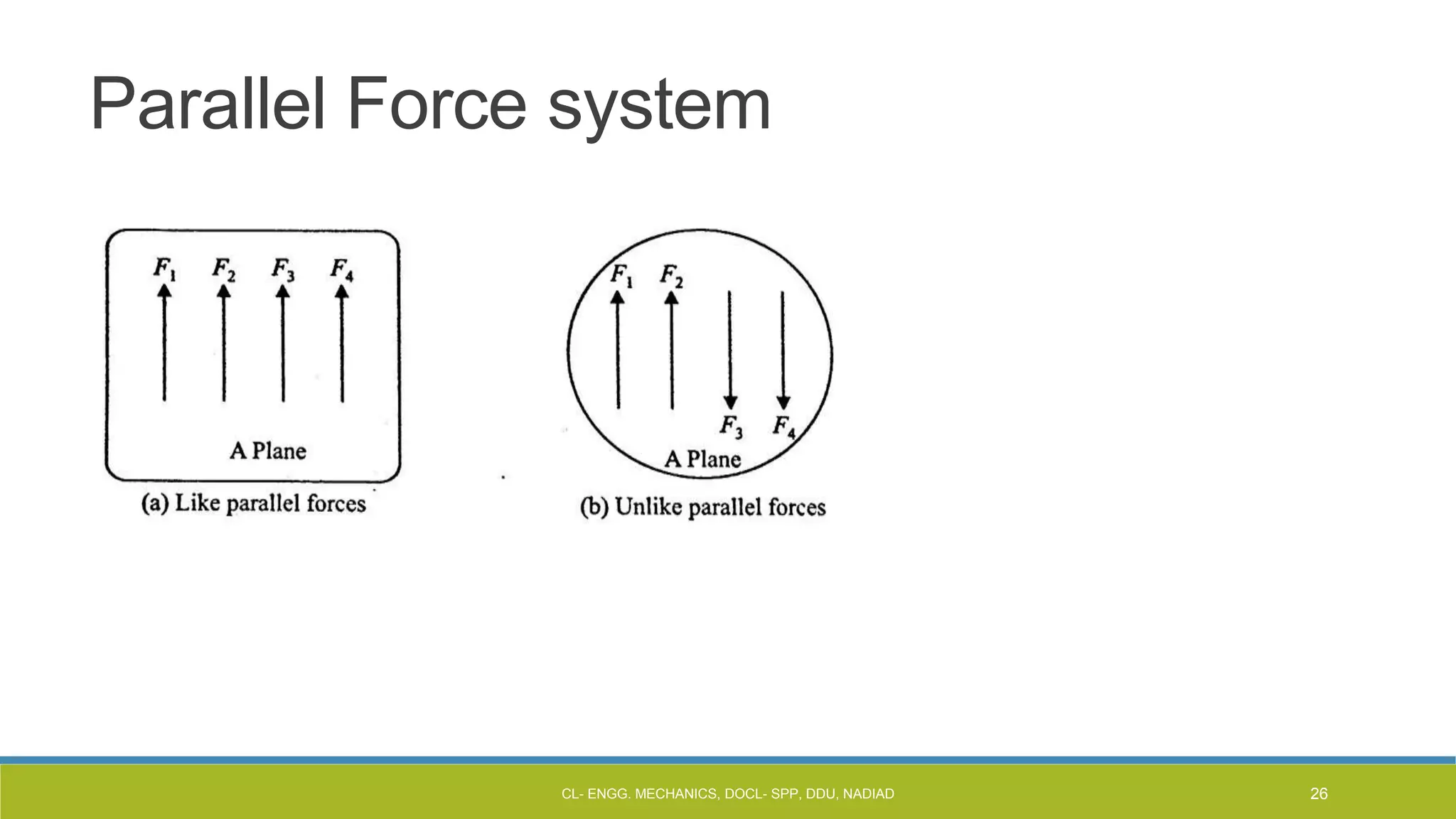
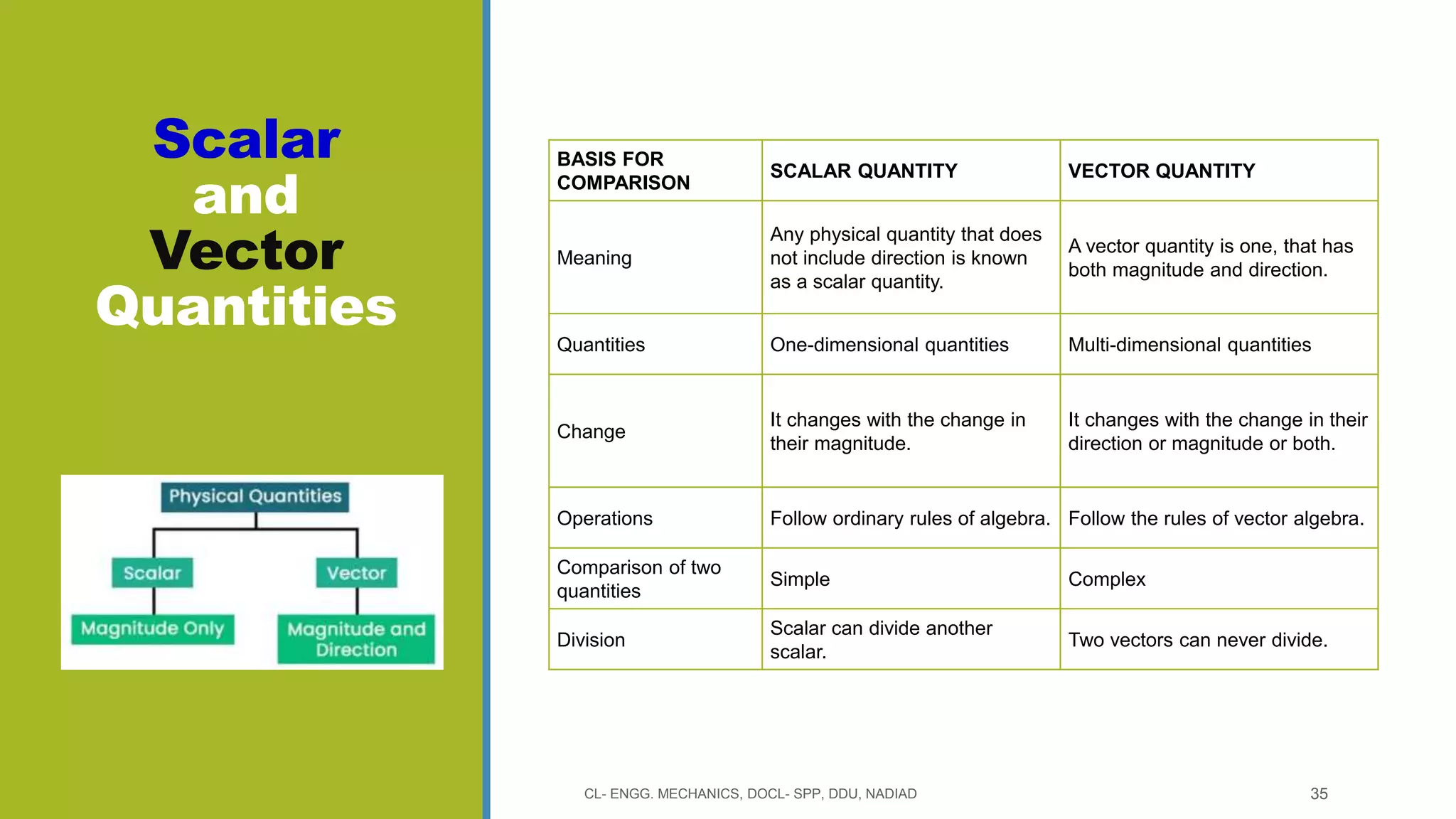
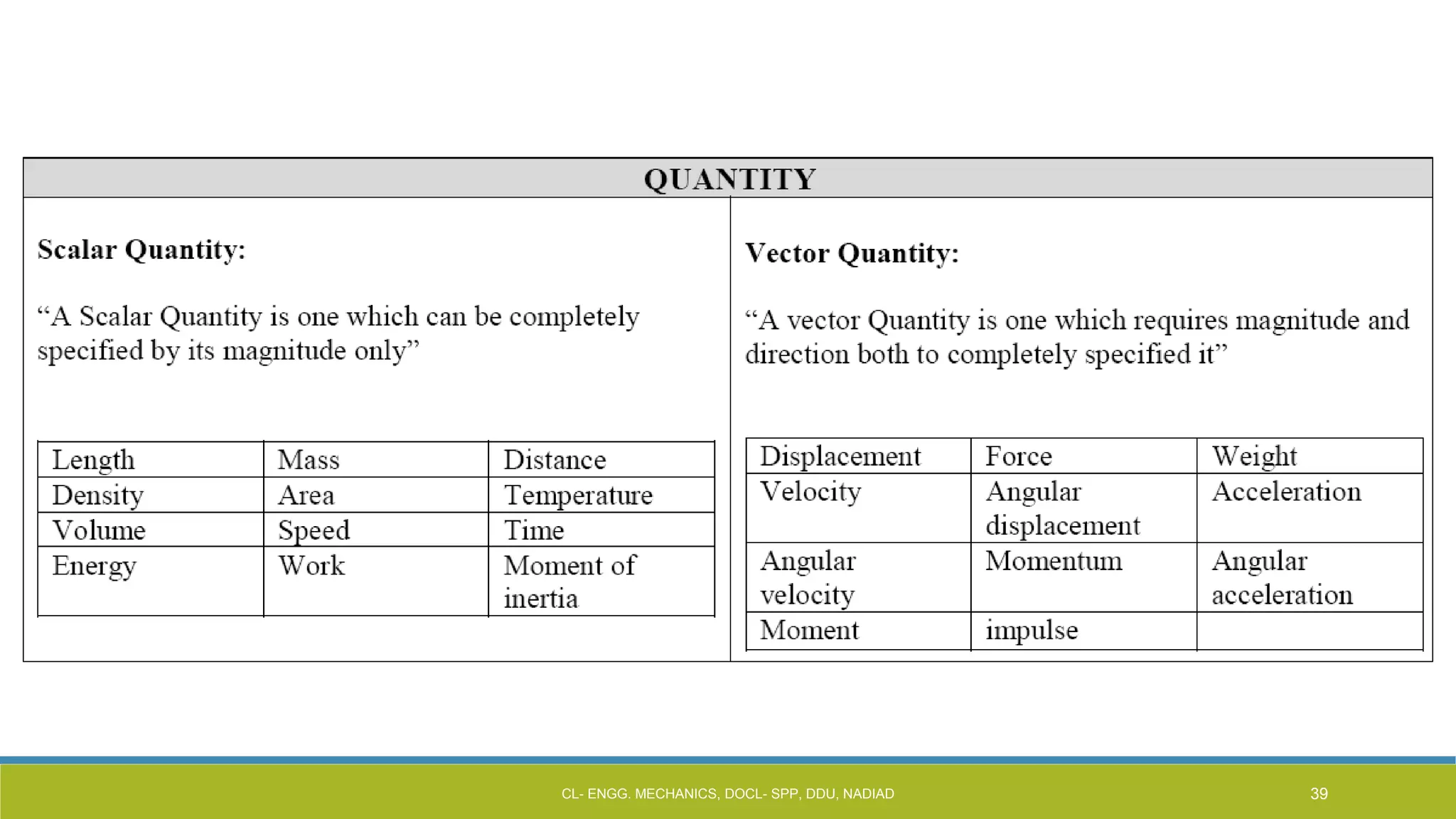
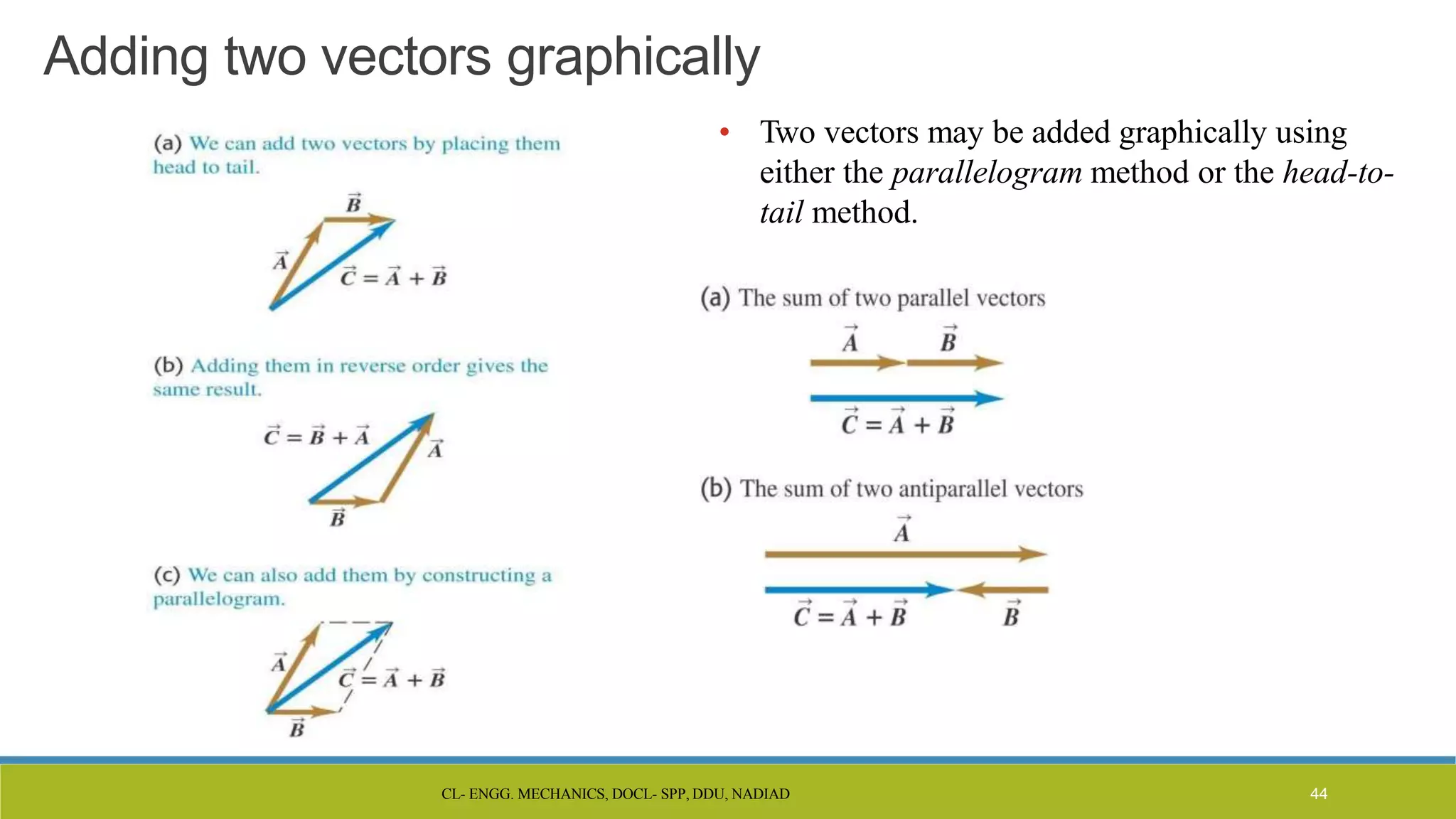
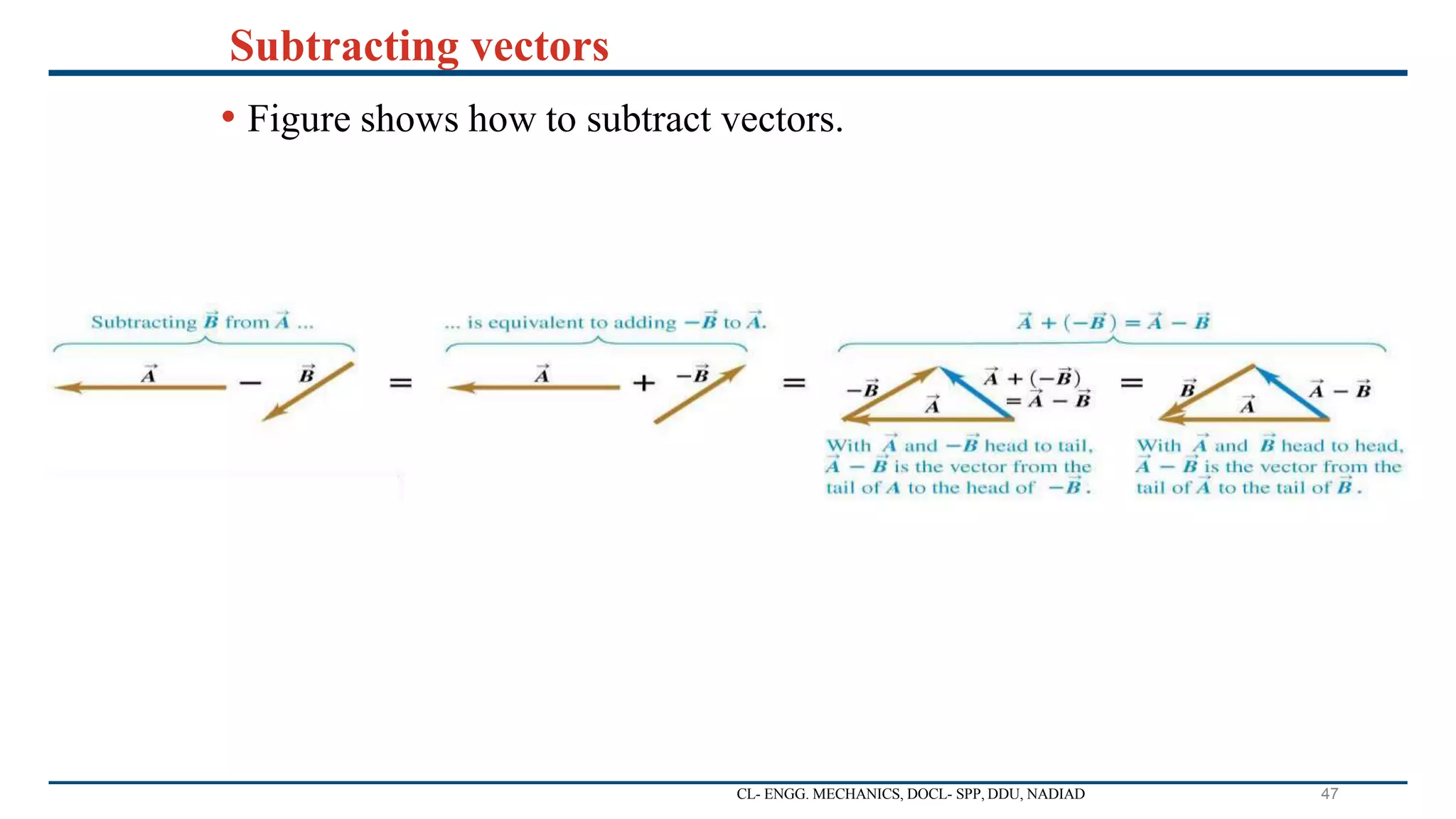
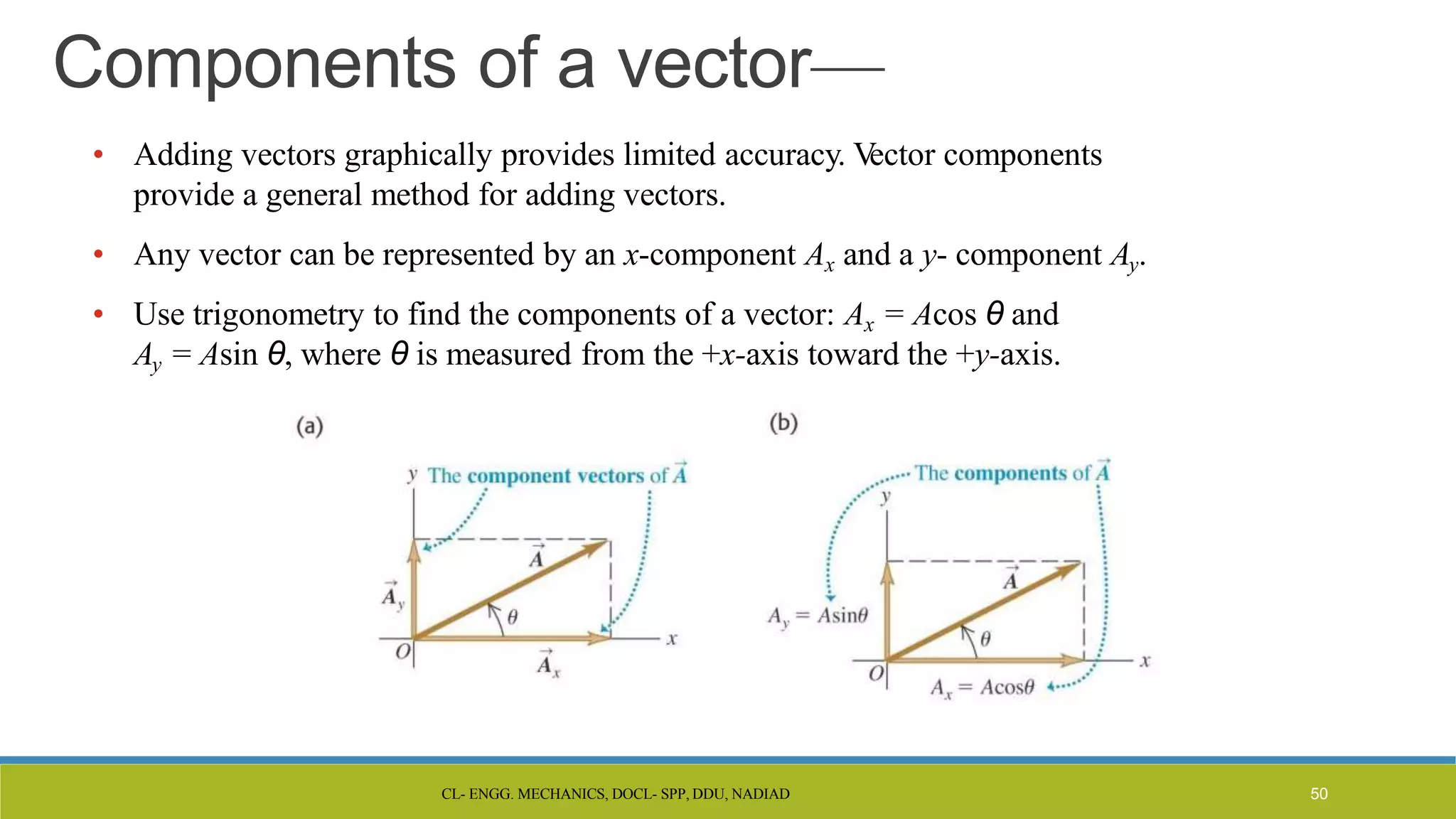
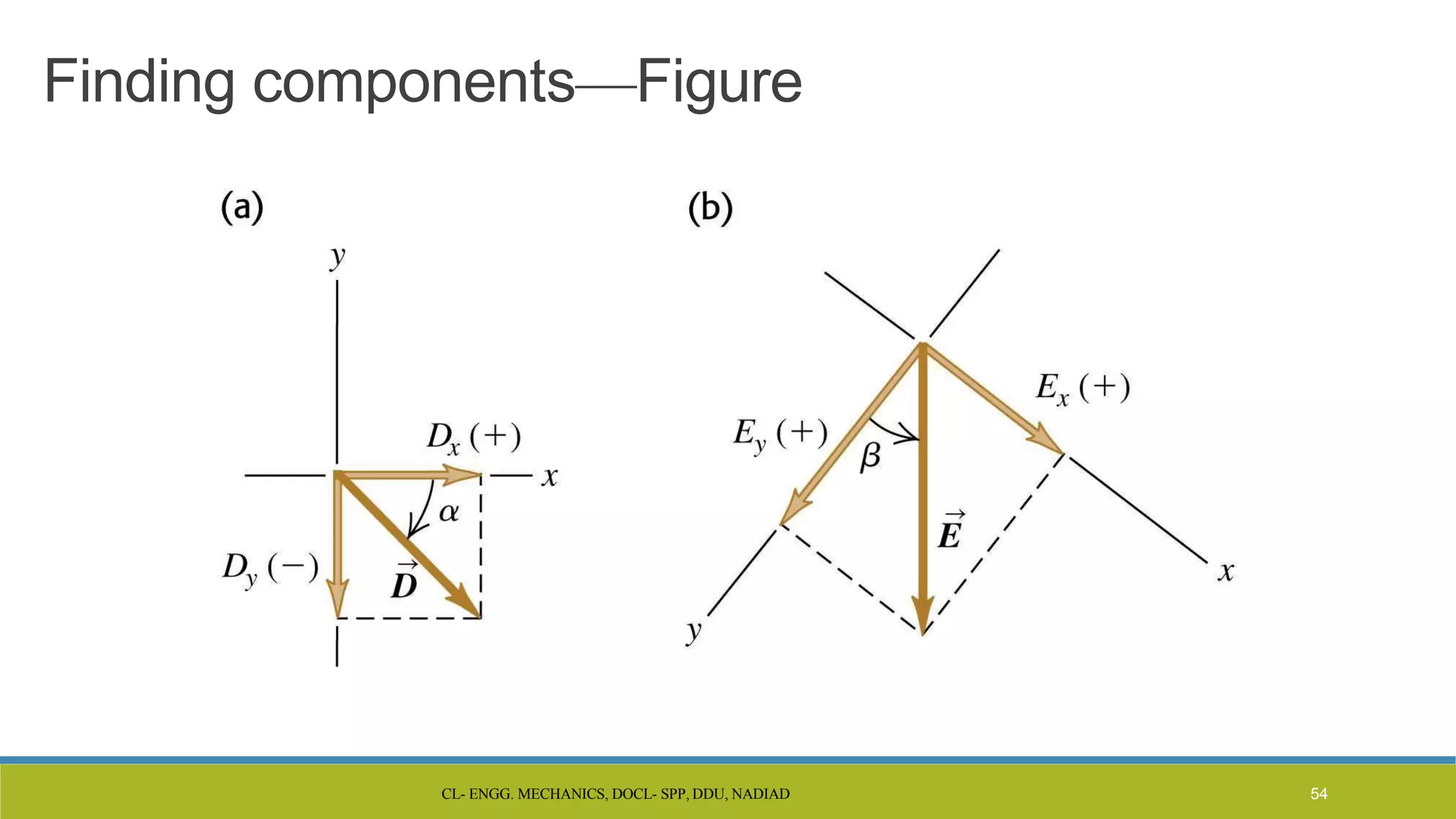
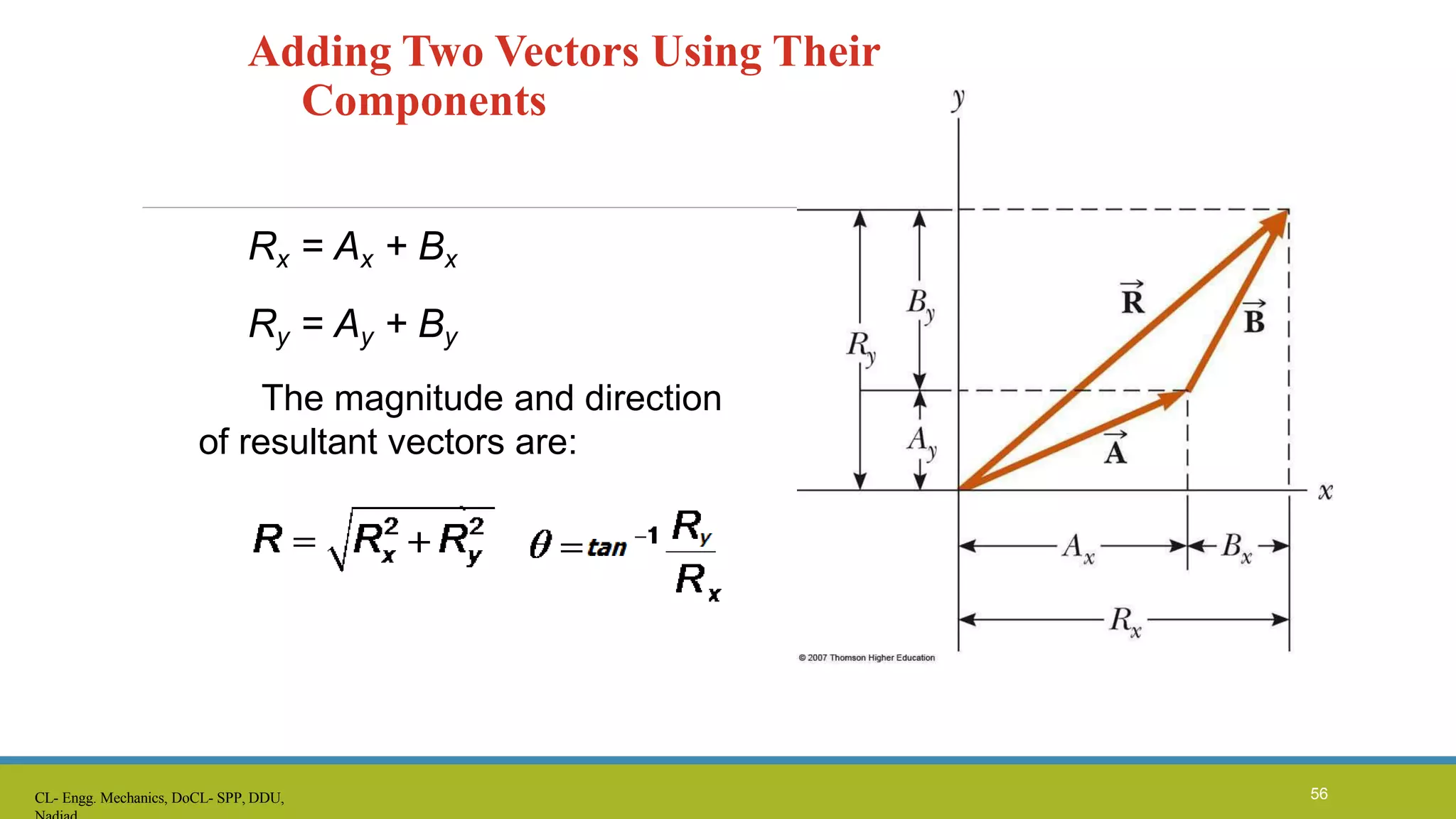
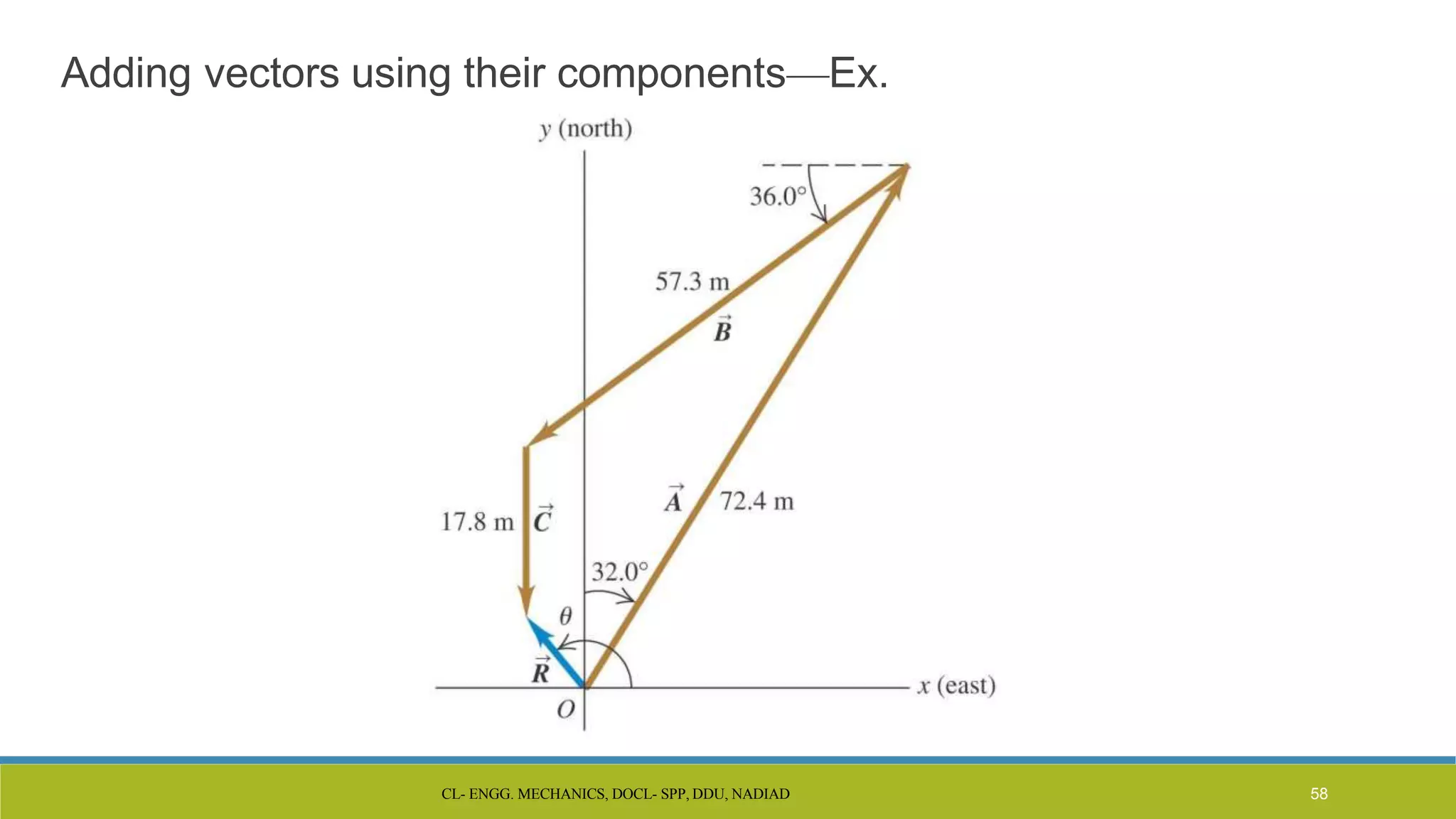
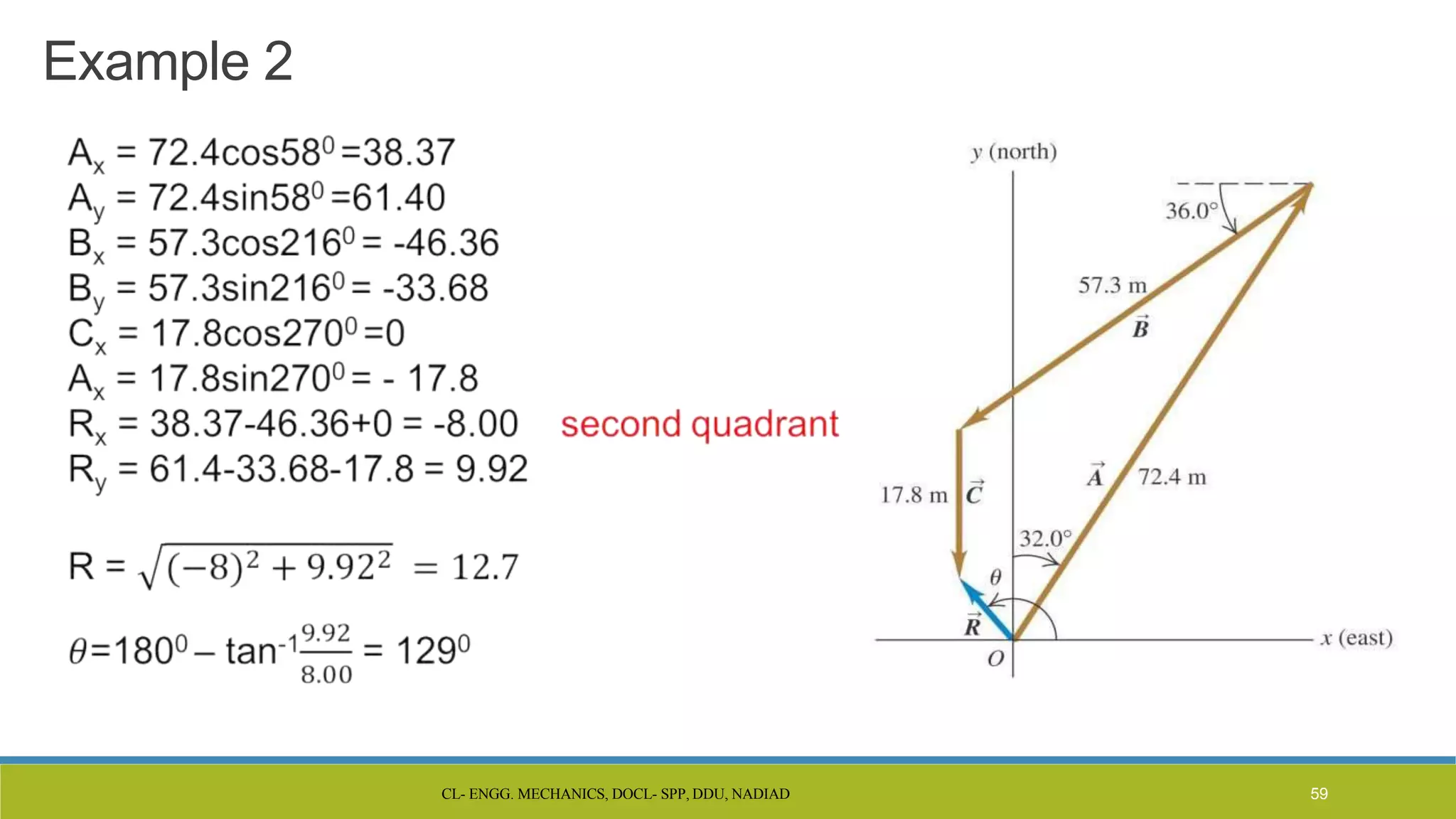
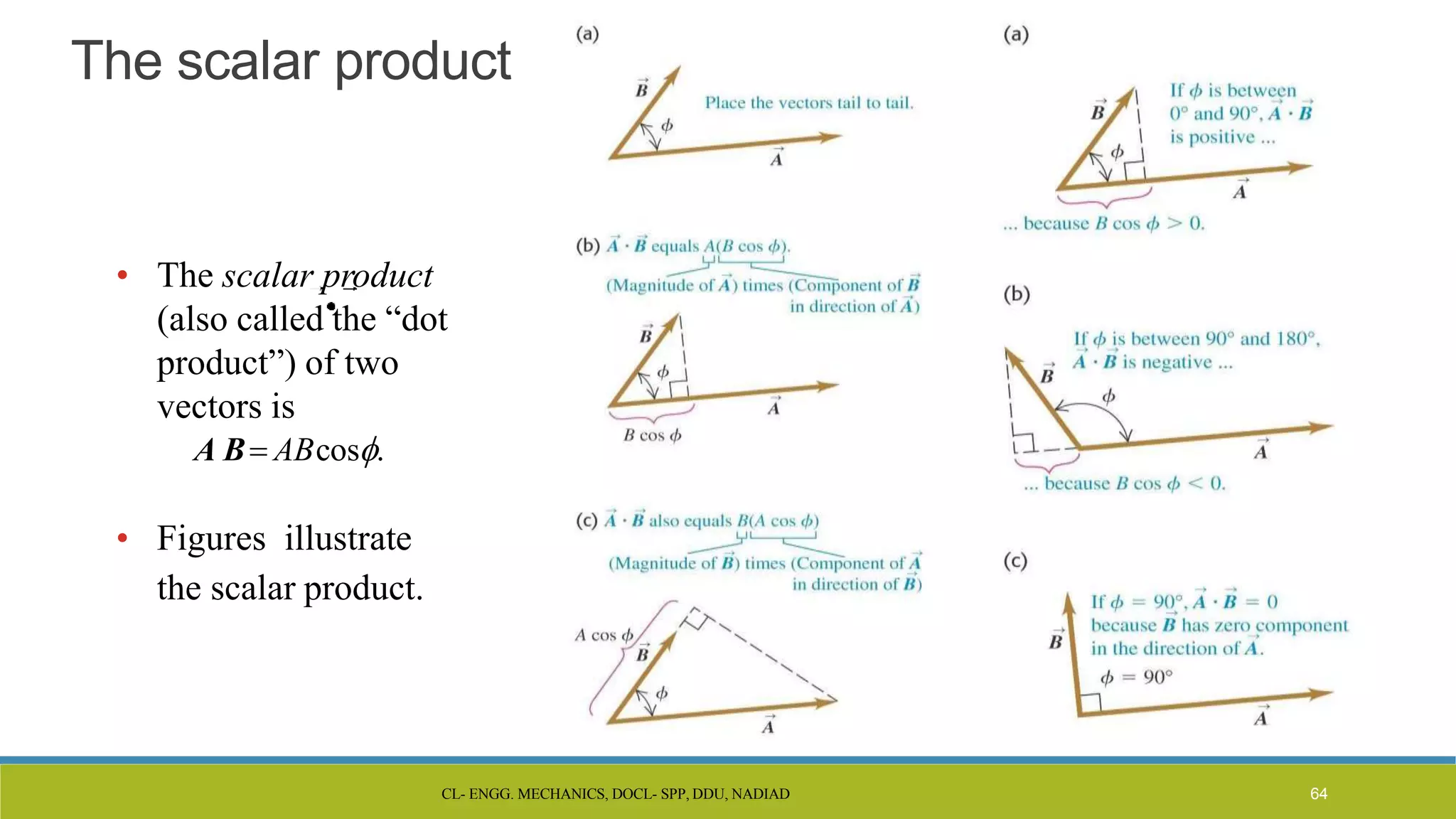
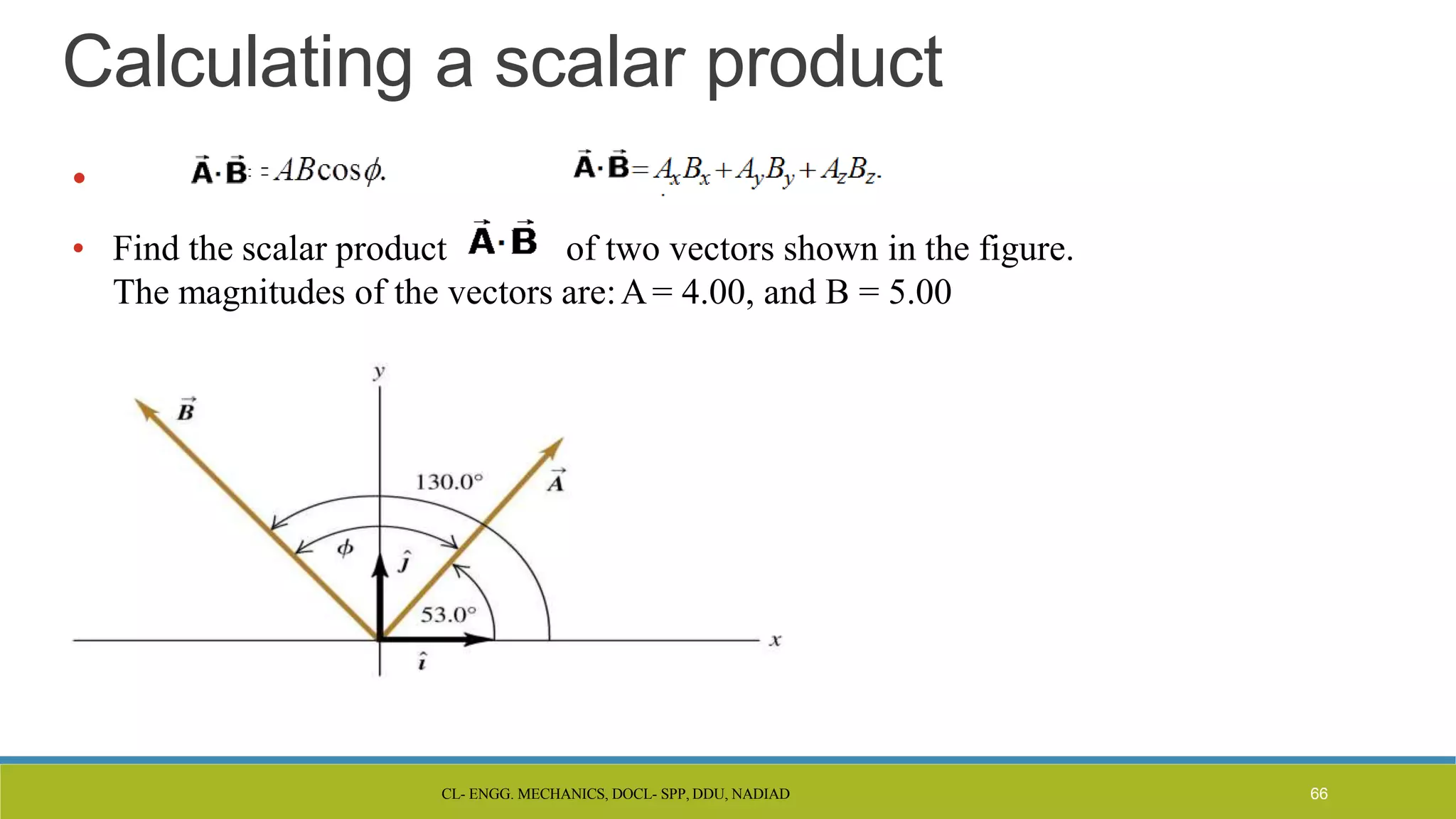
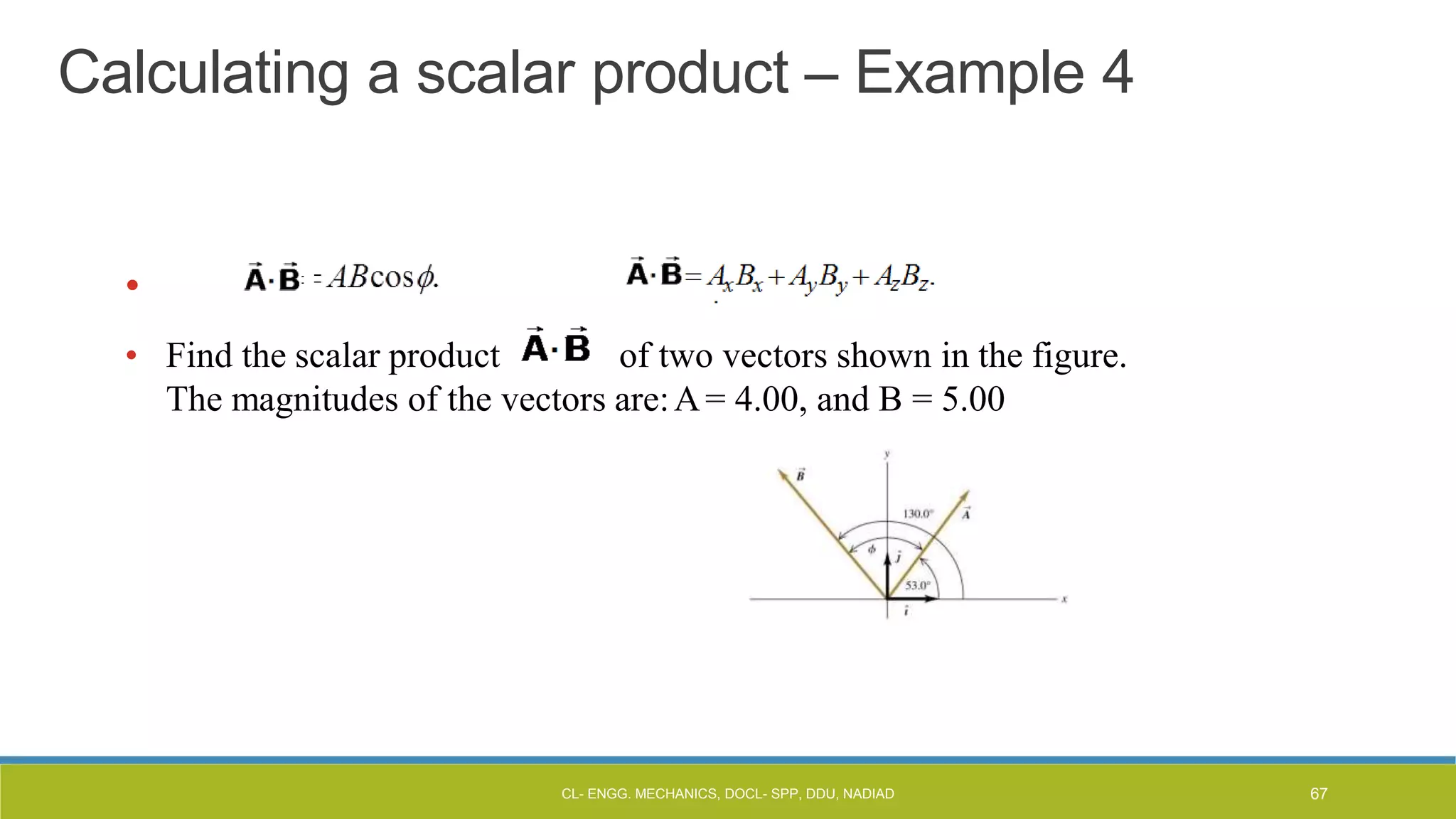
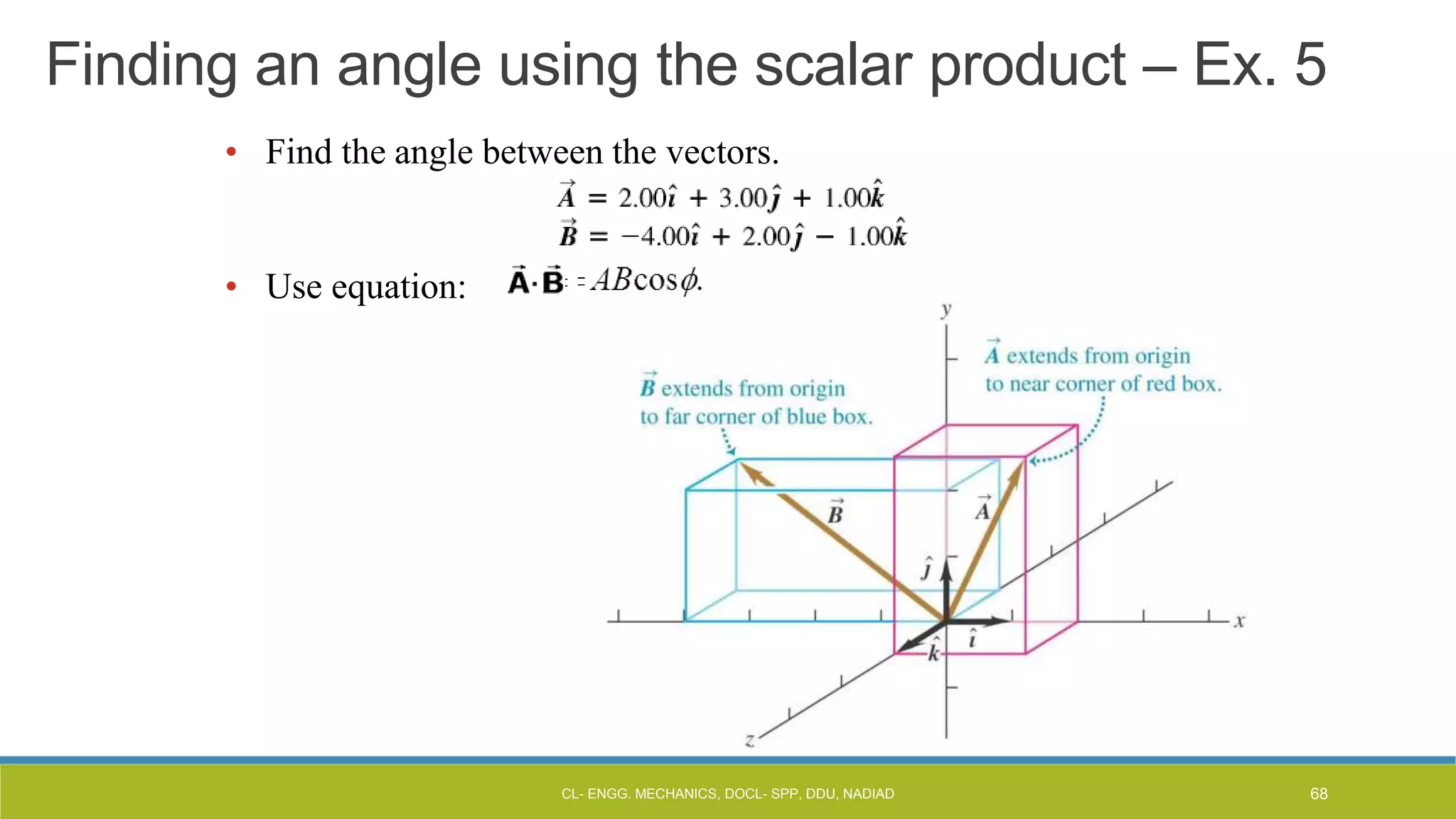
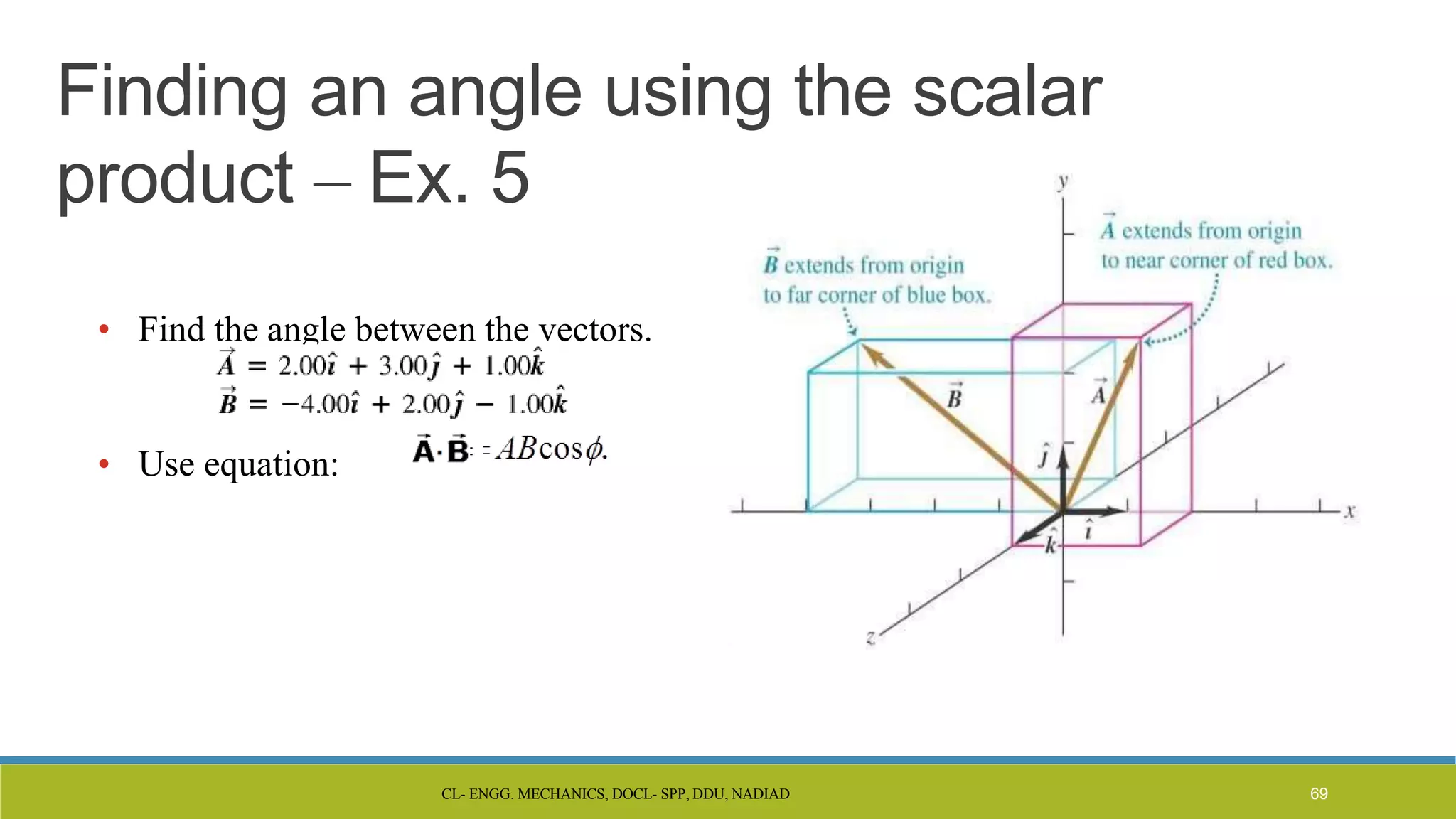
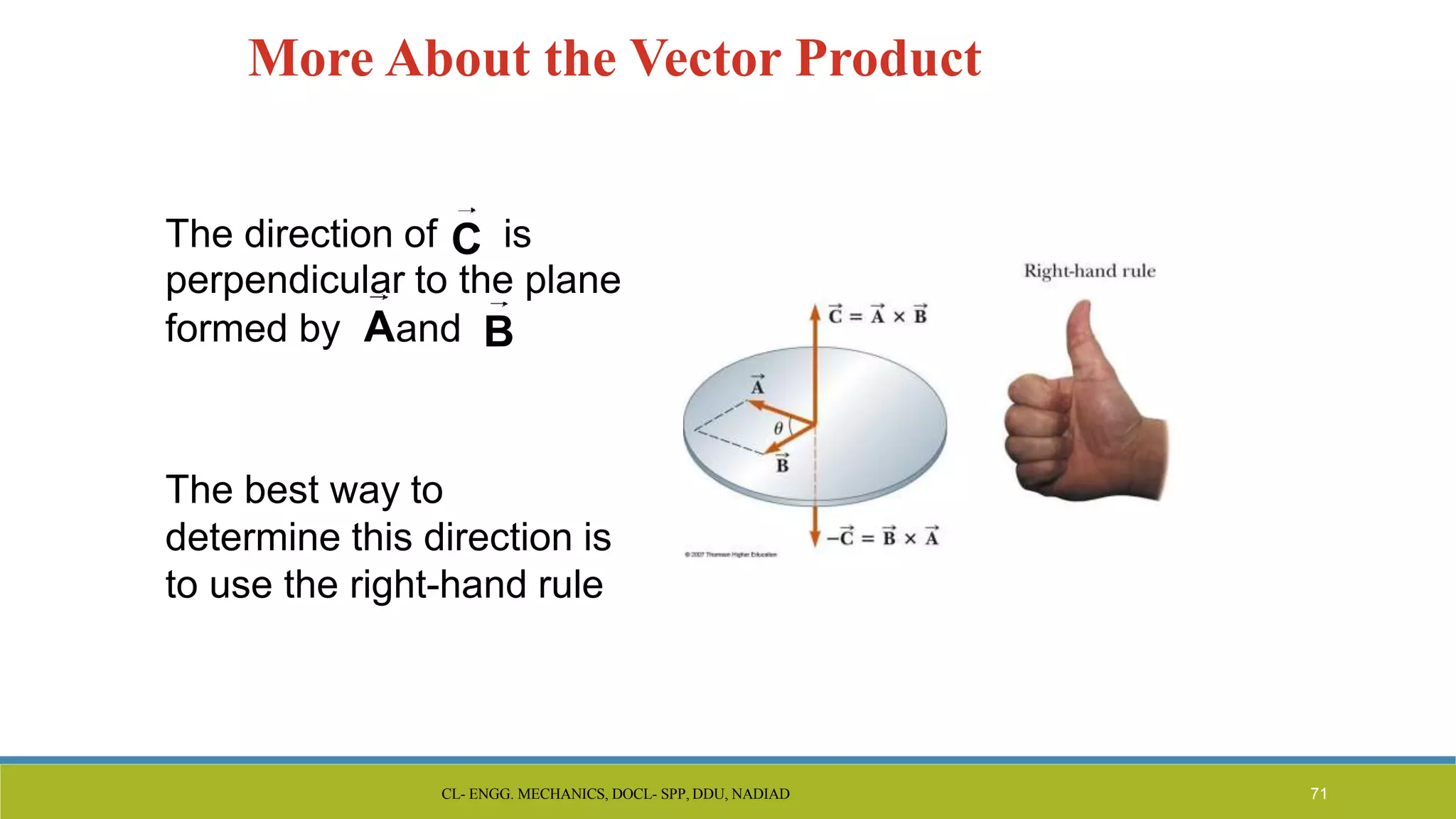
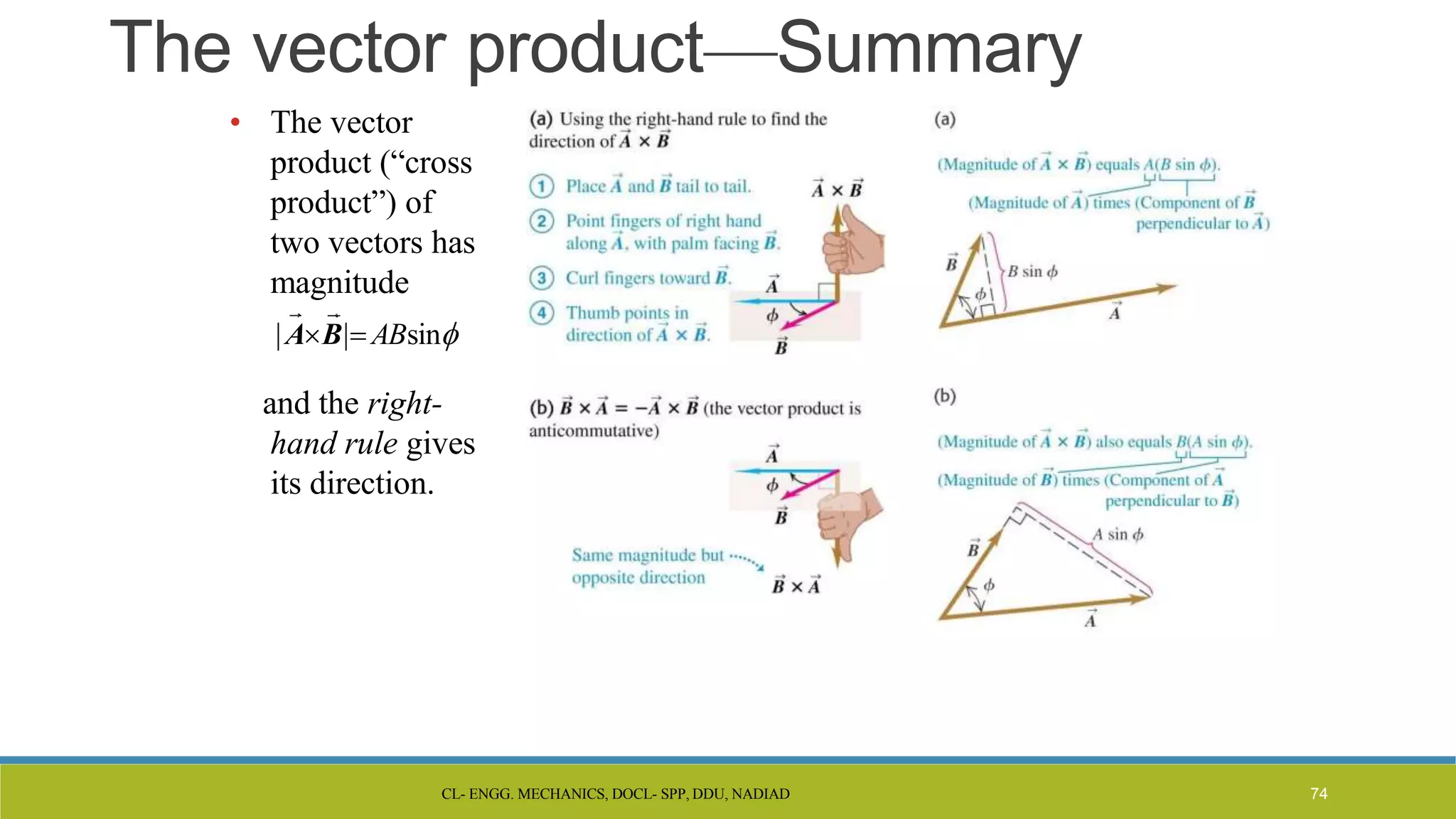
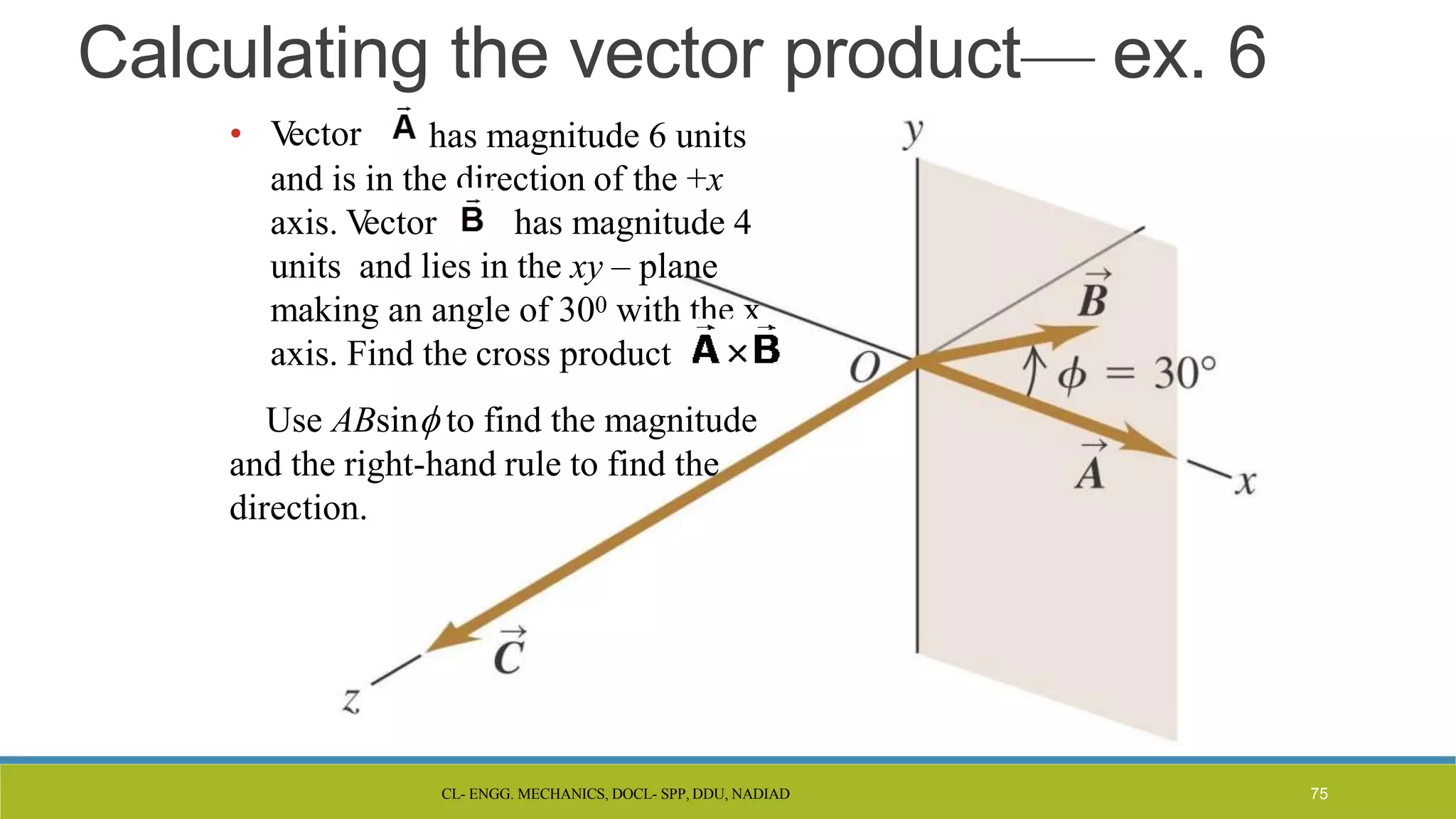
The document is a lecture presentation on engineering mechanics, covering fundamental concepts such as statics, dynamics, and the importance of force and its characteristics. It explains the SI system of units, idealizations in mechanics, and the differentiation between scalar and vector quantities, along with methods to add and subtract vectors. Additionally, it introduces the concepts of unit vectors and their application in vector calculation.