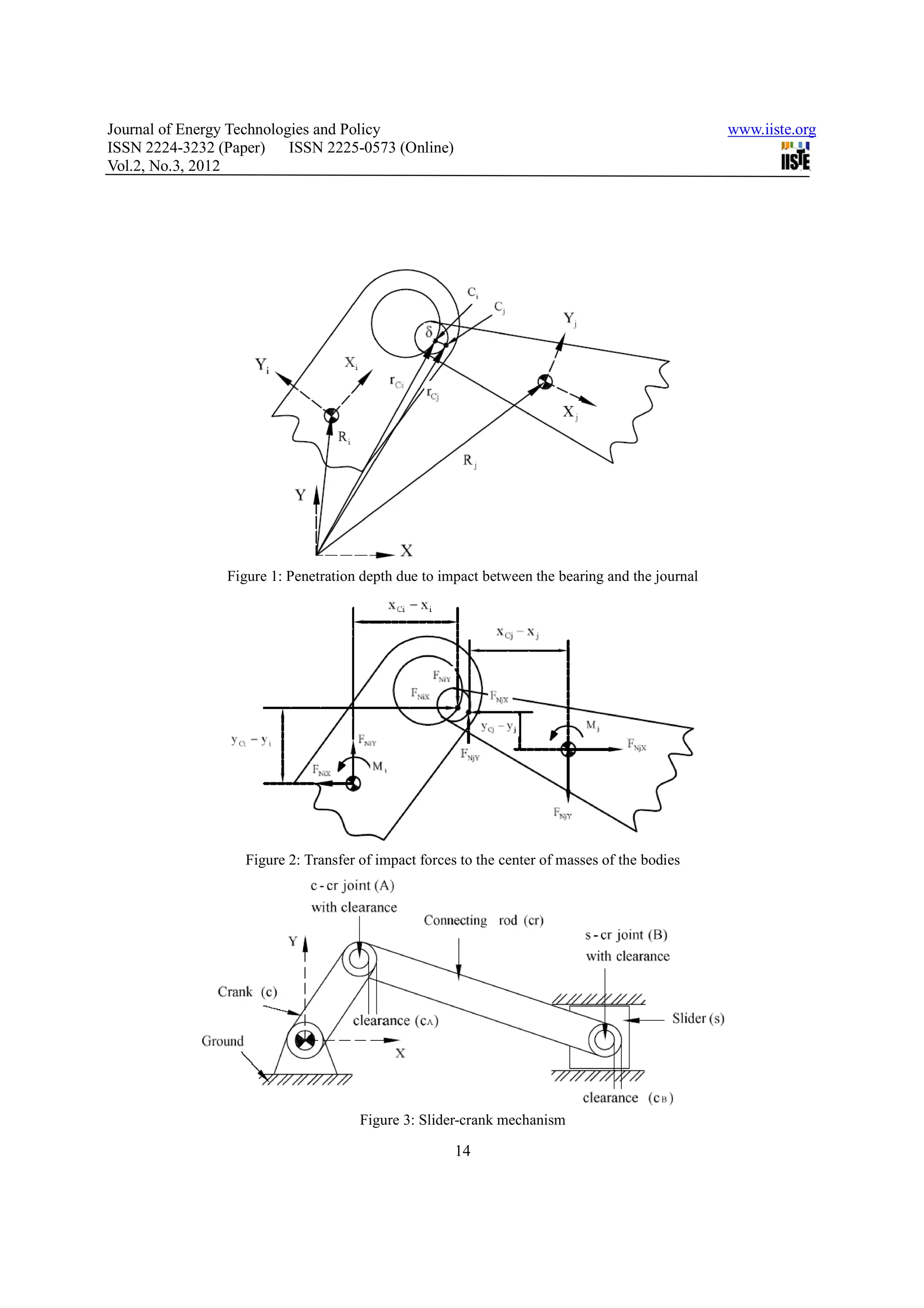
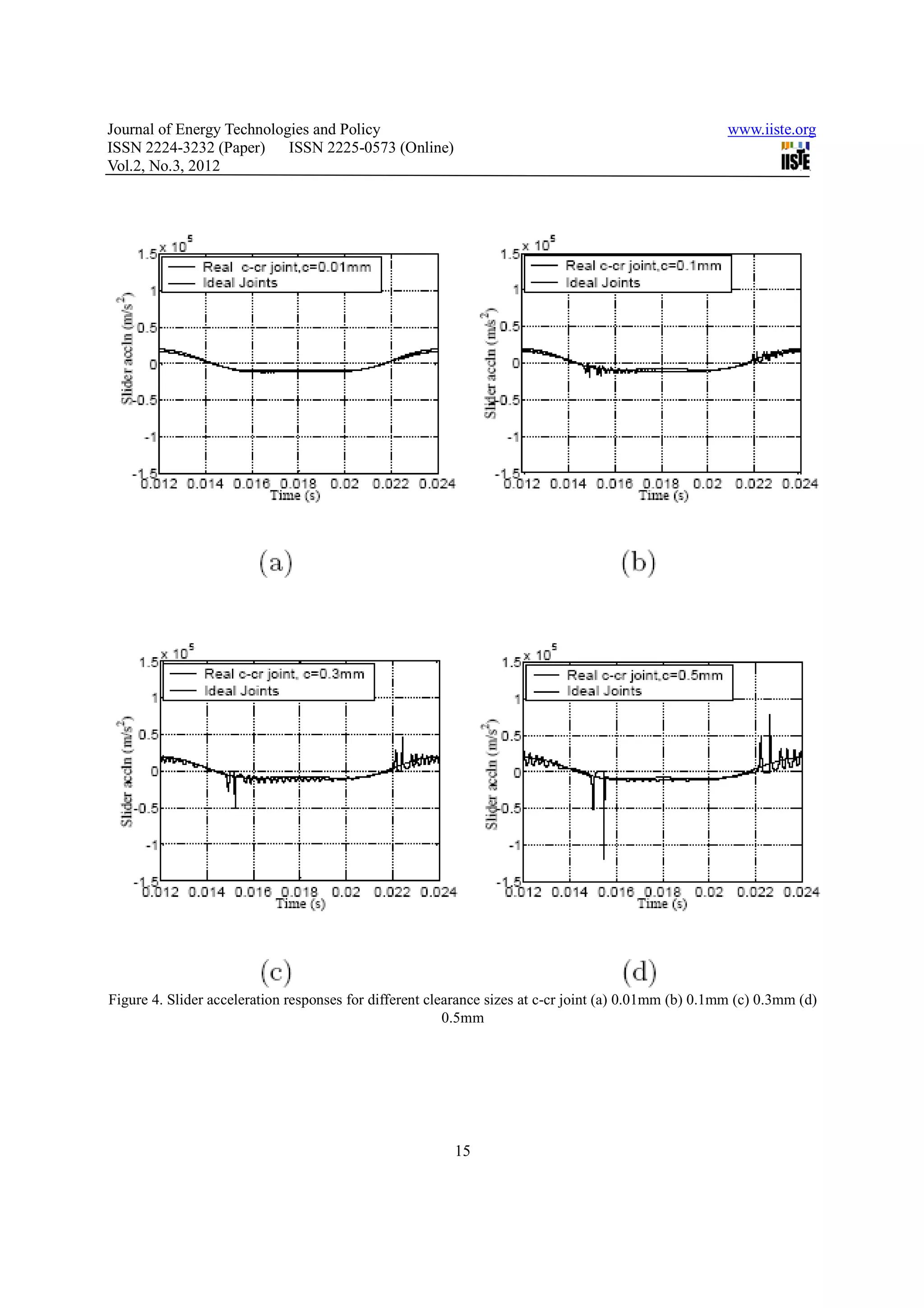
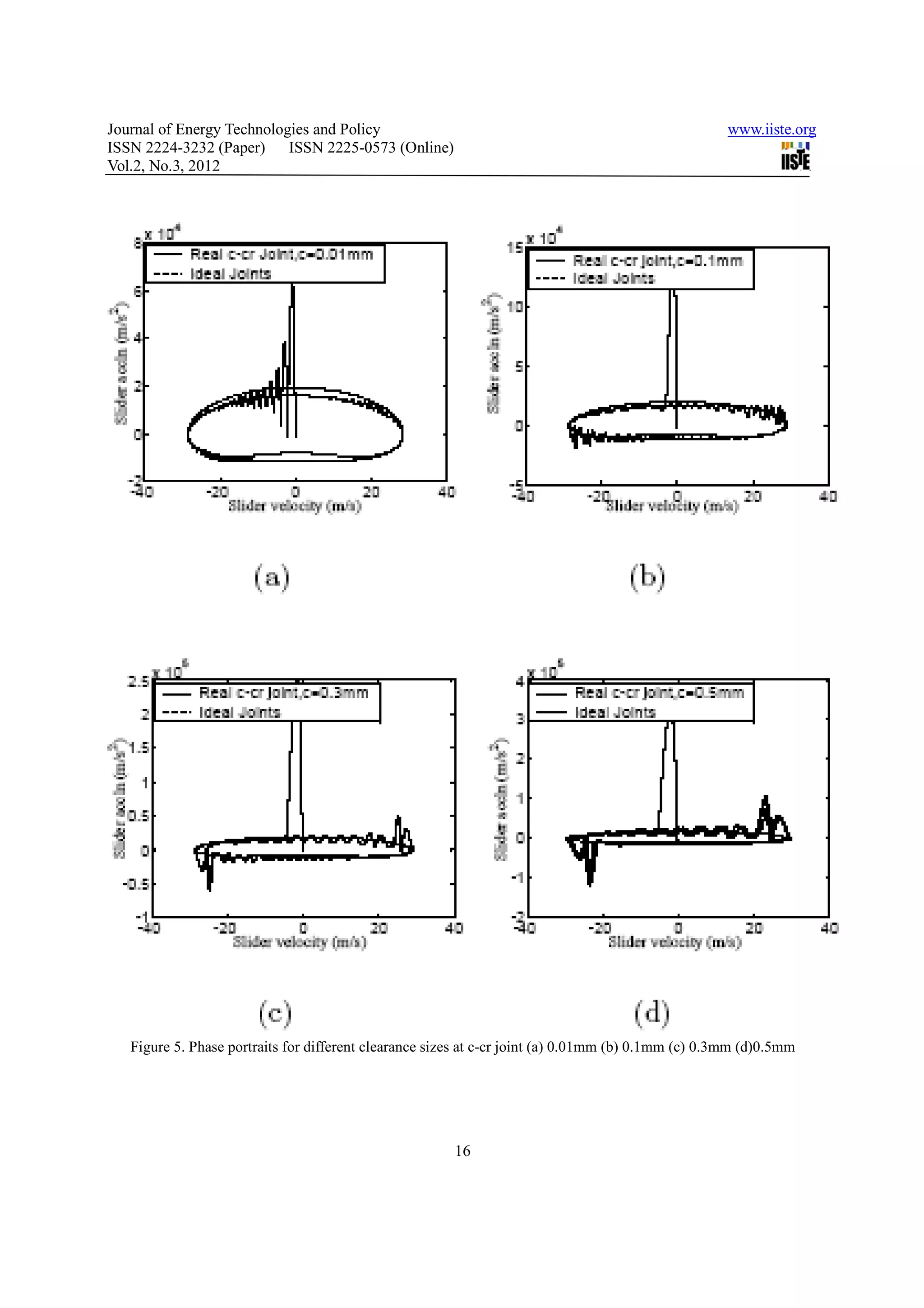
The document discusses the effects of clearance size on the dynamic response of multi-body systems with revolute clearance joints located in different positions. It numerically investigates how clearance size affects the overall dynamic characteristics. A slider-crank mechanism is used as a demonstration case, examining the effects of clearance size between the crank-connecting rod joint and connecting rod-slider joint separately. The results show that different joints have different sensitivities to clearance size, so the dynamic behavior of one clearance joint cannot represent the whole system. The location and size of the clearance joint both influence the accuracy of predicting the system's dynamic responses.