This document summarizes an SEIR model used to model the 2014-2015 Ebola outbreak in West Africa. The model tracks susceptible, exposed, infectious, and recovered individuals over time. It was able to fit reported case and death data from Guinea, Sierra Leone, and Liberia reasonably well. When updated with more recent data, the model still fit dynamics in Guinea and Sierra Leone but overestimated cases in Liberia. Parameter values like transmission rate and decay rate varied between countries and initial assumptions in the original model were too simplistic.

1. Outbreak of Ebola Presentation
By
RYAN AHEARN, CHARLTON CALLENDER,
GERARD TRIMBERGER, JESSE WALES
422/522 FINAL PROJECT
COMPLETED AT
THE UNIVERSITY OF WASHINGTON SEATTLE
DECEMBER 2015

2. Contents
1 Introduction 2
2 Model 6
3 Reproduction of Results 12
3.1 Paper Model vs Our Model . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
4 Novel Results 17
5 Conclusions 20
6 Appendix 23
1

3. Chapter 1
Introduction
As of December 2nd
, 2015 there have been a total of 28,601 cases as reported by the CDC.
11,300 of those cases ended in death. The outbreak in West Africa is believed to have been
caused by a child in Guinea who was infected by a fruit bat in December 2013. However, the
cases were not reported as an Ebola outbreak until March 2014. Unlike previous outbreaks
which began in rural areas of Africa, the most recent outbreak that Althaus’ paper discusses
began in the densely populated border region between three countries: Guinea, Sierra Leone
and Liberia.
These countries have weak health systems, they tend to lack human and infrastructure
resources, and have recently emerged from long periods of war and instability. Infections are
caused by contact through infected blood or other bodily fluids, as well as re-use of needles,
or physical contact with infected dead. This includes contact with linens, and surfaces that
the infected may have touched with their fluids. Traditional West African burial practices
2

4. are that families wash the deceased and that they are to be buried in the villages in which
they were born. The infection spread quickly as infected bodies were moved to towns via
taxis that operated in these densely urban areas. This greatly contributed to the massive
spread due to the high mobility of the persons there. As stated by Moore, ”Many burial
practices have to be curtailed if an outbreak is going to be contained.” On August 8, 2014,
the World Health Organization Director-General declared the West Africa outbreak a Public
Health Emergency of International Concern under the International Health Regulations.
The first Ebola outbreak began in Yambuku, Zaire in September 1976. Until 2014, it
was the largest outbreak on record with a total of 318 cases and 280 deaths. Blood samples
from an infected Belgian nun working in Zaire made it to a low-security lab in Belgium
contained within a thermos full of mostly melted ice. One of the sample vials had broken,
so the other was fished out of the blood and broken glass to be examined. Many tests
were completed using the samples, but the tests for the usual suspects (yellow fever, Lassa
fever, and Typhoid) all came back negative. It wasn’t until they infected lab animals did
they learn they were dealing with something that was ”quite deadly.” Shortly thereafter, the
World Health Organization ordered all of the samples at the Belgian lab to be moved to a
high-security lab in England. However, one of the supervisors for the project took a vial to
keep for examination at the Belgian facility, but dropped it onto a colleague’s foot where the
vial shattered. Luckily, none of the investigators were infected due to their ignorance of the
disease.
The virus was finally identified using an electron microscope (See Figure (1.1)). It was
3

5. Figure 1.1: EBOV under a microscope
found to be similar to the Marburg virus which also causes a hemorrhagic fever. When sci-
entists first flew to Zaire, they still were uncertain how the virus is passed between humans.
All precautions were taken, but the suits were quickly discarded due to the heat. There, it
was discovered that the virus was spread by the hospitals themselves through contaminated
needles.
Ebola is part of the family of Filoviridae viruses. Ebola contains several strains that
affect humans: Ebola-Zaire, Ebola-Sudan, Ebola-Ivory Coast (Tai Forest), and Bundibugy.
The 2014-2015 outbreak was caused by the Ebola Zaire virus which is also the deadliest
of the strains with an 80-90% death rate. Symptoms include weakness, muscle, joint, and
abdominal pains; headache, sore throat, nausea, then they begin to bleed from the eyes and
have red spots under the skin due to damaged blood vessels, the cough and vomit bloody-
foam as their lungs and guts weaken, then the virus begins to cause severe organ damage
targeting the spleen, kidneys, and liver which causes bloody diarrhea (See Figure (1.2)).
4

6. Figure 1.2: Symptoms caused by Ebola Virus
The incubation period, or the time interval from infection to onset of symptoms, is from
2 to 21 days. People are not contagious until they develop symptoms and infections can only
be confirmed through laboratory testing. There is no cure or treatment for Ebola. Those
infected can only be made comfortable, contained, and given intravenous fluids.
5

7. Chapter 2
Model
The model used in Estimating the Reproduction Number of Ebola Virus (EBOV) During
the 2014 Outbreak in West Africa [1] is an SEIR model. Before introducing the disease,
the entire population, N, is in the susceptible, S, category and are equally likely to catch
the virus. An individual who contracts Ebola then enters the incubation period, E, where
symptoms are not apparent and they are not yet infectious. Then the individual enters an
infectious stage, I, once they begin to show symptoms and can now infect others. Finally,
the individual either enters the recovered stage, R, or dies. Individuals belonging to stage
R are no longer susceptible to the virus as they have gained a temporary immunity to the
virus. C is the number of cases at a certain time. D is the number of fatalities at a certain
time.
The model ignores the initial vector of transmission from bats to humans. It only consid-
ers human to human transmission. However, it does not take into account infections caused
6

8. by the infectious dead. The model also does not take into consideration those that have
recovered and have spent enough time in R to pass back into S. It also assumes an N of
106
individuals, which is negligible since the stages are represented as ratios of the total
population.
One last assumption that needs to be mentioned when creating the model for such dy-
namic behavior is that of the difference between the model start point and that of the data.
It is often, if not always the case, that the first reported cases of an outbreak are long after
the first initial case. Most of the time, it is impossible to trace the outbreak back to its
original source. For this reason assumptions are made in Althaus’ model, as well as ours.
We assume that the first case (i.e. I0 = 1 and C0 = 1) in Guinea occurred on December 01,
2013 and the first cases in Sierra Leone and Liberia were on April 15, 2014. These values
were estimated from the Althaus figures. A ”tshift” value was calculated by subtracting
this ”assumed start date” from that of the date from the first reported cases. This value
was then used to appropriately scale the time axis to position the data at the correct time
point along the time axis. For example, the first reported data point in the Guinea region
was on 3/25/14 with 86 cases and 59 deaths. However, this data point does not represent
the first case that is assumed in our model. Therefore, a ’tshift’ value must be calculated
between the date of this point and the assumed start date (i.e. 12/01/13). This shift allows
us to plot the data point corresponding to 86 cases and 59 deaths further down the time
axis. A similar shift is applied to all data sets for all regions and allows for a more accurate
correlation between model predictions and real life data.
7

9. 


dS
dt
=
−β(t)SI
N
dE
dt
=
β(t)SI
N
− σE
dI
dt
= σE − γI
dR
dt
= (1 − f)γI
dC
dt
= σE
dD
dt
= fγI
(2.0.1)
8

10. Parameters Definition
S Susceptible, i.e. they can be infected
E Exposed, i.e. they are infected, but not yet contagious
I Infectious and transmitting
R Recovered
C Number of cases
D Number of fatalities
N Total population; S + E + I + R
β(t) = βe−k(t−τ)
transmission rate over time
β transmission rate over time in absence of intervention
f fatality rate
k =
ln(2)
τ1/2
rate at which the transmission rate decays
σ per-capita infectious rate and
1
σ
= average incubation period
γ per-capita death rate and
1
γ
= average infectious period
τ1/2 time until transmission rate is 50% of initial value
τ
time when control measures are introduced (assumed to be 0
for this model)
R0 =
β
γ
basic production number
Re =
β(t)S
γN
≈
β(t)
γ
effective production number; number of people infected per
infectious case; if Re < 0, the outbreak is ”contained”
9

11. This model used data as reported by the CDC from March 2014 until August 2014. The
model fit very well with the progression of reported number of cases and fatalities. Our
modification to the model was to introduce the data that has been updated by the CDC to
be as recent as possible. The figures produced using Althaus’ models from the paper are
Figure (2.1) and Figure (2.2).
Figure 2.1: Dynamics of the 2014 EBOV outbreaks in Guinea (left), Sierra Leone (center)
and Liberia (right). The data of the cumulative numbers of infected cases are shown as red
circles and the cumulative numbers of infected deaths as black squares. The lines represent
the best-fit model to the data (See legend). Note: the scale of the x-axis differs between
each of the countries.
10

12. Figure 2.2: Effective reproduction number (Re) of EBOV in Guinea (left), Sierra Leone
(center) and Liberia (right). This model assumes that β decays exponentially due to the
introduction of control measures. In Guinea and Sierra Leone, the effective reproduction
number has dropped to around unity by the end of May/July 2014, respectively (dashed
lines). In Liberia, Re remains unchanged by end of August 2014. Note: the scale of the
x-axis differs between countries and
1
γ
= 5.61 days.
11

13. Chapter 3
Reproduction of Results
The reproduction of Althaus’ figures models are Figure (3.1) and Figure (3.2), respectively.
Do to the difference between programming languages, there are slight differences in the axes.
Althaus’ figures were produced using the statistical programming language R. Ours was, of
course, made using MATLAB. All assumptions discussed for the Althaus model stands true
for our recreations and additions to the model.
The fminsearch MATLAB command was utilized in our code to solve for optimized beta,
f, and k parameters for the model’s system of differential equations. The ebola min function
was created to solve for the sum-square error (SSE) between the WHO data points and the
model predictions at those corresponding time points (i.e. those of corresponding to each
WHO point). fminsearch accepts the function ebola min which solves for error and the initial
guesses for the beta, k, and f values. The command then solves for the optimal parameter
values such that ebola min returns the lowest value for SSE.
12

14. Figure 3.1: Dynamics of the 2014 EBOV outbreaks in Guinea (left), Sierra Leone (center)
and Liberia (right). The data of the cumulative numbers of infected cases are shown as red
circles and the cumulative numbers of infected deaths as black circles. The lines represent
the best-fit model to the data (See legend). Note: the x-axis represents a different starting
date between countries.
3.1 Paper Model vs Our Model
SEIR model plotted by Althaus was consistent with data released by the CDC and WHO
of total cases reported, confirmed, and probable as well as total reported, confirmed, and
probable deaths for the time period March 2014-August 2014. Updated information about
the totals from each country was introduced to the model. Though the model itself was still
able to accurately represent the number of cases and deaths, changes were needed in the
parameters for each country. By comparing the two models we can make some inferences
about how the first model holds up when the new data is introduced. These comparative
models are Figure (3.3) and Figure (3.4) which explore the infections’ dynamics and Re,
13

15. Figure 3.2: Effective reproduction number (Re) of EBOV in Guinea (left), Sierra Leone
(center), and Liberia (right). This model assumes that β decays exponentially due to the
introduction of control measures. In Liberia, Re remains unchanged by end of August 2014.
Note: the x-axis represents a different starting date between countries and
1
γ
= 5.61 days.
respectively.
Looking at Figure (3.3) (left and center), we can see that the predictions made by Al-
thaus were too low for both Guinea and Sierra Leone. Althaus’ paper made the assumption
that intervention measures taken at the time would cause the infection to be contained be-
fore 2015. What they could not have predicted was the unaccountable spread of the disease
through contaminated dead and surfaces as well as the inhumane treatment of the quaran-
tining process. There were stories of quarantined areas that were protected by armed guards
without influx of fresh food or water for the duration of the quarantine. Figure (3.4) (left
and center) tells us that unity was not reached until about January 2015 which was several
months after the Althaus prediction. The dashed line is an indication of when those infected
will infect one other person and the disease is beginning to decline.
14

16. For Liberia, the predictions differs from the two papers unlike Guinea and Sierra Leone.
As mentioned in the paper, the k value for Liberia is set at 0*, in which the ”*” indicates the
unreasonableness of this assumption. Due to this, Althaus’ model predicted an uncontrolled
spread of EBOV in Liberia. When compared with current data, it is strikingly obvious how
unrealistic this assumption was for the long run as the increase was too large to reasonably
plot (See Figure (3.3), right). In Figure (3.4) (right), the Althaus model never reached a
level of unity implying that those that were sick kept infecting those around them. Numer-
ical comparisons of β, f, and k for all three countries are made in the following Numerical
Comparisons Table.
Numerical Comparisons of Parameters β, f, and k in Althaus Paper and Updated Model
Althaus, 2014 Guinea Sierra Leone Liberia
β 0.27 0.45 0.28
f 0.74 0.48 0.71
k 0.0023 0.0097 0*
Updated, 2015 Guinea Sierra Leone Liberia
β 0.24 0.31 0.34
f 0.67 0.30 0.45
k 0.000816 0.0024 0.0032
15

17. Figure 3.3: Our model vs. Althaus model dynamics of the 2014-2015 EBOV outbreaks in
Guinea (left), Sierra Leone (center), and Liberia (left). The data of the cumulative numbers
of infected cases are shown as red circles and the cumulative numbers of infected deaths as
black circles. The solid lines represent the best-fit model to the data for the updated model
and the dashed lines represent the predicted fit as determined by the Althaus paper(See
legend). Note: the x-axis represents a different starting date between countries.
Figure 3.4: Our models’ Re of EBOV outbreak in Guinea (left), Sierra Leone (center), and
Liberia (right). The models assume that β decays exponentially due to the introduction of
control measures. Note: the x-axis represents a different starting date between countries
and
1
γ
= 5.61 days. Red represents the Althaus model and black is our Re. The dashed line
represents the line of unity at y = 1.
16

18. Chapter 4
Novel Results
Figure (4.1) visually sums up the outbreaks over their entire course as there have not been
any new, confirmed cases since mid-November of 2015. For the total number of cases and
deaths including all three countries, β = 0.3271, k = 0.0025, and f = 0.4065. The ”Total
plot” (Figure (4.1) bottom right) assumes a pooled population but still is able to map the
course of the outbreak fairly well for not considering any spacial separation and equal mixing
between the populations of the countries.
For each country, the fatality rate was reduced after introducing more information. Con-
sidering the Althaus model mostly included information from the beginning of the outbreak,
it is understandable that intervention measures may not have had time to be visually effec-
tive within the model. Though, over time, the intervention measures obviously helped get
the outbreaks under control. One example of this is the fatality rate itself; EBOV has been
recorded as having a fatality rate of around 80-90%. However, by the end of the outbreaks, f
17

19. was less than 45% for the total number of cases. This is even lower than the average fatality
rate of any other strain of Ebola!
18

20. Figure 4.1: Our model dynamics of the 2014-2015 EBOV outbreaks in Guinea (top left),
Sierra Leone (top right), Liberia (bottom left) and totals between all three countries (bottom
right). The data of the cumulative numbers of infected cases are shown as red circles and
the cumulative numbers of infected deaths as black circles. The lines represent the best-fit
for the model (See legend). Note: the x-axis is based on the number of days after the initial
case and represents a different starting date between countries.
19

21. Chapter 5
Conclusions
A study of the parameters β, k, and f were done to see what their behavior would be if
they were increased. These comparisons can be seen in Figure (5.1). Reading the Figure
from left to right, we can make the following inferences: that as β approaches one, both the
number of infected cases and fatalities rises dramatically even with only a small change; as
f is increased, only the number of fatalities increases because f does not affect the number
of S or I; as k is increased, the number of infected and the number of fatalities is greatly
reduced. These graphs allow us to visualize how the transmission term, β, fatality term, f,
and transmission decay rate, k, can affect the overall population.
It may seem too obvious, but it is worth mentioning that attempting to model biologi-
cal data cannot capture how it will actually happen. In general, this can be due to many
reasons which includes, but is not limited to, human error, mutations, immigration, and
unpredictable human reactions. It is especially hard to predict the outcome of any situation
20

22. based on limited knowledge of the situation. The Althaus’ model is a wonderful one to use
for a biological phenomenon such as the spread of EBOV, though the parameters needed to
be changed to more accurately represent the real world data released by the CDC.
Though the Althaus model fit the data at the time very well, it was not able to predict
that the intervention at the time was not enough to control the outbreaks. Althaus’ model
predicted that the outbreaks in Guinea and Sierra Leone would be contained well before
January 2015 and that the outbreak in Liberia would spread without stopping. With their
limited data set, and considering the level of previous outbreaks, it seemed unlikely that the
outbreaks would get much worse.
Looking at Figure (4.1), it is clear that the outbreaks did not begin to level off until over
a year after the initial infections began. From this, we can infer that any models using data
before this time would most likely not be able to accurately predict the outcome, as the
trend would not yet be seen until around this one year mark. It is probable that the Althaus
model could not begin to accurately represent the outbreaks as there had never been one
like it before with this particular disease. However, if such an outbreak would happen again,
the updated model could be useful in determining the dynamics of EBOV. Both past and
present data is useful in making a more accurate model.
The particular way in which this code is designed is to pass in almost any data set of
dates, cases and deaths, and solve for optimal values for the beta, k, and f parameters.
Because of this ability to be transmissible, it would be interesting to solve this system of
differential equations for other data sets. For example, the Althaus paper mentions that
21

23. they base their sigma and gamma values (i.e. infection and incubation period) on a 1995
paper on a similar Ebola strain in Congo. In future work, we could take the data set for that
outbreak and pass it through our models to ensure that we solve for the same parameter
values. We could also examine how well this model predicts behavior for other strains of
Ebola and even other diseases.
Figure 5.1: Left: As β approaches one, the number of infected persons and fatalities rises.
Center: As f increases, the number of deaths increases. However, f does not affect the
number of S or I. Right: As k is increased, the number of infected and the number of
fatalities is greatly reduced.
22

24. Chapter 6
Appendix
Ebola Class Presentation.m
clear all;close all;clc
%Set max time point
Tmax=609;
%Time range where want solution
tspan=0:1:Tmax;
%create vector of initial values for different countries
%1-Guinea, 2-Sierra Leone, 3-Liberia
s(1,1).Guinea = ’Guinea’;
23

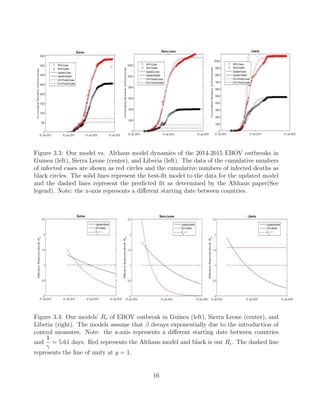
25. s(2,1).SierraLeone = ’Sierra Leone’;
s(3,1).Liberia = ’Liberia’;
countries= fieldnames(s);
beta=[.27,.45,.28]; %.27 Guinea; .45 Sierra Leon; .28 Liberia
k=[.0023,.0097,0]; % .0023 Guinea; .0097 Sierra Leon; 0* Liberia
tau=0; %Model Assumption-control measure began after appearance of first infected case;
sigma=1/5.3; %days; based on data from Congo
gamma=1/5.61; %days; ” ” ” ” ”
fata=[.74,.48,.71]; %.74 Guinea; .48 Sierra Leon; .71 Liberia
%Specify INITIAL VALUE
N= (1 ∗ 106
); %total population
S 0 = (N − 1); E 0 = 0; I 0 = 1; R 0 = 0; C 0 = 1; F 0 = 0; %proportional populations
%initial SEIR=[S 0 ; E 0; I 0; R 0]*N; %set initial pop. for each stage
initial SEIR=[S 0 ; E 0; I 0; R 0; C 0; F 0]; %set initial pop. for each stage, used when need
cases and fatalities
country data = xlsread(’previous-case-counts.xlsx’); % data from CDC, previous case
counts
% data from 3/25/14 - 11/25/15, 609 days
24

26. figure()
for i=1:3
param = [N,beta(i),k(i),tau,sigma,gamma,fata(i)];
%Call ODE solver ode45 as follows
% function F=my ebolafun(t,SEIR,N,beta,k,tau,sigma,gamma,f)
[t,SEIR]=ode45(@my ebolafun,tspan,initial SEIR,[],param);
%plot solution components vs. time
%figure(i)
subplot(3,3,i)
plot(t, SEIR(:,1)) ; hold on
plot(t, SEIR(:,2))
plot(t, SEIR(:,3))
plot(t, SEIR(:,4))
plot(t, SEIR(:,5))
plot(t, SEIR(:,6))
xlabel(’Time, t(days)’,’FontSize’,10)
ylabel(’Population of each Stage (S,E,I,R)’,’Fontsize’,10)
title([’Model Population Dynamics for ’,num2str(countriesi)],’Fontsize’,10)
legend(’S-Susceptible’,’E-Exposed’,’I-Infected’,’R-Recovered’,’C-Cases’,’F-Fatalities’,’Location’,’Best’)
25

27. R e=zeros(length(tspan),1);
for j=1:length(tspan)
beta t = beta(i)*exp(-k(i)*(j-tau));
R e(j)=beta t/gamma;
end
subplot(3,3,i+3)
plot(t,R e)
xlabel(’Time from initial breakout, t(days)’,’FontSize’,10)
ylabel(’Effective reproduction number, R e’,’Fontsize’,10)
title([num2str(countriesi)])
subplot(3,3,i+6)
t data=41723:1:42332; % same serial dates as case data
plot(country data(:,1),country data(:,2*i),’ro’); hold on;
plot(country data(:,1),country data(:,(2*i+1)),’ko’); hold on;
axis manual %keep the axis fixed now
plot(t data, SEIR(:,5),’r-’); hold on; % cases
plot(t data, SEIR(:,6),’k–’); hold on; % fatalities
%axis auto
xlabel(’Time, t(days)’,’FontSize’,10)
ylabel(’Individuals’,’FontSize’,10)
26

28. title([num2str(countriesi)])
legend(’Cases’, ’Deaths’, ’Cases Model’, ’Deaths Model’,’Location’,’northwest’)
datetick(’x’, 2)
end
my ebolafun.m
function dSEIR dt=my ebolafun(t,SEIR 0,p)
%t is the time
%SEIR is the state vector
%F is the velocity vector
%N is total pop. size = S+E+I+R
%beta is transmission rate in absence of control interventions
%k: the transmission rate was assumed to decay exponentially at rate k
%tau is the time that control measures were introduced tau <= t
N = p(1); beta = p(2); k = p(3); tau= p(4); sigma= p(5); gamma= p(6); f = p(7);
%Therefore, betat is the effect of the control measures on the
%transmission rate over time, t
beta t= beta ∗ exp(−k ∗ (t − tau));
%sigma is 1/”the average duration of incubation”
%gamma is 1/”the average duration of infectiousness”
27

29. %f is the fatality rate
S=SEIR 0(1);
E=SEIR 0(2);
I=SEIR 0(3);
R=SEIR 0(4);
dS dt=-beta t*S*I/N;
dE dt=beta t*S*I/N-sigma*E;
dI dt=sigma*E-gamma*I;
dR dt=(1-f)*gamma*I;
dC dt=sigma*E;
dF dt=f*gamma*I;
%dSEIR dt=[dS dt; dE dt; dI dt; dR dt];
dSEIR dt=[dS dt; dE dt; dI dt; dR dt; dC dt; dF dt];
end
% function R e=my ebolafun2(S,N,gamma,beta t)
% R e=beta t*S/(gamma*N);
% end
28

30. min ebola.m
function SSE=min ebola(p0)
beta=p0(1);
k=p0(2);
f=p0(3);
% parameters that are fixed
tau=0;
sigma=1/5.3;
gamma=1/5.61;
N= (1 ∗ 106
); %total population
param=[N;beta;k;tau;sigma;gamma;f];
country=8:9;
% Guin=2:3; Lib=4:5; SLeo=6:7; Tot=8:9;
country data = xlsread(’previous-case-counts.xlsx’); % data from CDC, previous case counts
CD data=country data(:,country); % only using guinea data for now
t data = country data(:,1);
%Set max time point
Tmax=max(t data);
29

31. %Time range where want solution
tspan=0:1:Tmax;
%Specify INITIAL VALUE
S 0 = (N − 1); E 0 = 0; I 0 = 1; R 0 = 0; C 0 = 1; F 0 = 0; %proportional populations
initial SEIR=[S 0 ; E 0; I 0; R 0; C 0; F 0]; %set initial pop. for each stage, used when need
cases and fatalities
[t,SEIRCD output]=ode45(@my ebolafun,tspan,initial SEIR,[],param);
CD output = [t, SEIRCD output(:,5:6)];
% From our model, get the dates that we have data for
num timepts=length(t data);
same CD output=zeros(num timepts,2);
for i=1:num timepts
same CD output(i,:)=CD output(t data(i)+1,2:3);
end
err = CD data(:,1:2)-same CD output(:,1:2);
SSE = sum(sum(err.2
));
Ebola fit.m
30

32. clear all; close all; clc;
country=8:9;
% Guin=2:3; Lib=4:5; SLeo=6:7; Tot=8:9;
country data = xlsread(’previous-case-counts.xlsx’); % data from CDC, previous case counts
% country data = flipud(country data); % flip the data so that time is going from old to
new
CD data=country data(:,country); % only using guinea data for now
t data = country data(:,1);
%Set max time point
Tmax=max(t data);
%Time range where want solution
tspan=0:1:Tmax;
% parameters that can change, give them initial values
% beta=0.2238;
% k=0.0026;
% f=.74;
%optimized values after first pass:
beta=0.2801;
31

33. k= 0.0019;
f=.6662;
p0=[beta,k,f]; % initial guess for beta
% search for the parameters that give the minimum error to fitting our data
[p final,fits]=fminsearch(@ min ebola,p0);
beta=p final(1);
k=p final(2);
f=p final(3);
% now plot the data and model results using the fitted parameters we calculated
% use fitted parameters now
tau=0;
sigma=1/5.3;
gamma=1/5.61;
N= (1 ∗ 106
); %total population
param=[N;beta;k;tau;sigma;gamma;f];
%Specify INITIAL VALUE
S 0=(N-1); E 0=0; I 0=1; R 0=0; C 0=1; F 0=0; %proportional populations
32

34. initial SEIR=[S 0 ; E 0; I 0; R 0; C 0; F 0]; %set initial pop. for each stage, used when need
cases and fatalities
[t,SEIRCD output]=ode45(@my ebolafun,tspan,initial SEIR,[],param);
figure(1)
plot(t data, CD data(:,1),’ro’); hold on;
plot(t data, CD data(:,2),’ko’);
axis manual %keep the axis fixed now
plot(t, SEIRCD output(:,5),’r-’);
plot(t, SEIRCD output(:,6),’k–’);
xlabel(’time (days)’,’FontSize’,14)
ylabel(’Number of People in Population’,’FontSize’,14)
title(’Ebola in All 3 Countries’,’FontSize’,18)
legend(’WHO-Cases’,’WHO-Deaths’,’Predicted Case’,’Predicted Deaths’,’Location’,’Best’)
stability simulation.m clear all; close all;
%Parameters optimized from data in all three countries
beta0=0.3271; k0=0.0025; f0=0.4065;
sigma= 1/5.3; gamma= 1/5.61; tau= 0; N= (1 ∗ 106
); %set parameters
33

35. %Set max time point
Tmax=610;
%Time range where want solution
tspan=0:1:Tmax;
%Initially start with one infectious case
S 0=(N-1); E 0=0; I 0=1; R 0=0; C 0=1; D 0=0;
initial SEIR=[S 0 ; E 0; I 0; R 0; C 0; D 0];
n = 20; %number of points to range parameter over
%range beta, k and f from 1/2 parameter to 2 times parameter
beta range=linspace((beta0*0.5),(beta0*2),n);
k range=linspace((k0*0.5),(k0*2),n);
f range=linspace((f0*0.5),(f0*2),n);
CD vary=zeros(3,n); % initialize vector to store parameter, cases and deaths
%store the parameter being varied in the first row of CD vary
CD vary(1,:)=beta range;
%CD vary(1,:)=k range;
%CD vary(1,:)=f range;
34

36. for i=1:n;
%select the varied parameter
beta=beta range(i);
%k=k range(i);
%f=f range(i);
param=[N;beta;k0;tau;sigma;gamma;f0]; %store in one vector
[t,SEIRCD output]=ode45(@my ebolafun,tspan,initial SEIR,[],param);
%Get the last case and death from the SEIRCD output.
CD vary(2,i)=SEIRCD output(Tmax+1,5);
CD vary(3,i)=SEIRCD output(Tmax+1,6);
end
figure(1)
ax = gca;
plot(CD vary(1,:),CD vary(2,:),’r-’,’LineWidth’,4); hold on
plot(CD vary(1,:),CD vary(3,:),’k–’,’LineWidth’,4); hold on
xlabel(’beta’,’FontSize’,20)
ylabel(’Individuals’,’FontSize’,20)
title(’Ebola in all 3 Countries, Vary f’, ’FontSize’,20)
35

37. line([beta0,beta0],[0,max(max(CD vary))],’LineWidth’,4)
ax.LineWidth = 2;
ax.FontSize = 20;
legend(’Predicted Cases’, ’Predicted Deaths’,’beta from all 3 countries’,’Location’,’northwest’)
36

38. Bibliography
[1] Althaus CL. Estimating the Reproduction Number of Ebola Virus (EBOV) During the
2014 Outbreak in West Africa. PLOS Currents Outbreaks. 2014 Sep 2 . Edition 1. doi:
10.1371/currents.outbreaks.91afb5e0f279e7f29e7056095255b288.
[2] Bredow, Rafaela Von, and Veronika Hackenbroch. ”Interview with Ebola Discoverer
Peter Piot.” SPIEGEL ONLINE INTERNATIONAL. SPIEGEL ONLINE, 26 Sept.
2014. Web. 03 Dec. 2015. ¡http://www.spiegel.de/international/world/interview-with-
peter-piot-discoverer-of-the-ebola-virus-a-993111.html¿.
[3] Moore, Peter. ”The Little Book of Pandemics: 50 of the World’s Most Virulent Plagues
and Infectious Diseases.” Fall River Press, 2009: 29-31. Print.
[4] ”Modeling the Spread of Ebola.” Web. 09 Feb. 2015.
¡http://www.math.washington.edu/ morrow/mcm/mcm15/38725paper.pdf¿.
[5] ”Ebola Virus Disease.” World Health Organization. WHO, Aug. 2015. Web. 02 Dec.
2015. ¡http://www.who.int/mediacentre/factsheets/fs103/en/¿.
37

39. [6] ”Freqently Asked Questions on Ebola Virus Disease.” World Health Organization.
WHO, Aug. 2015. Web. 02 Dec. 2015. ¡http://www.who.int/csr/disease/ebola/faq-
ebola/en/¿.
[7] ”Previous Case Counts.” Center for Disease Control. CDC, 3 Dec. 2015. Web. 3
Dec. 2015. ¡http://www.cdc.gov/vhf/ebola/outbreaks/2014-west-africa/previous-case-
counts.html¿.
38