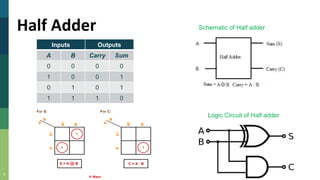
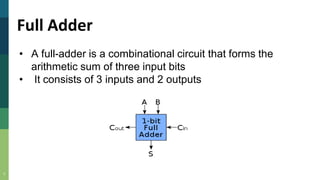
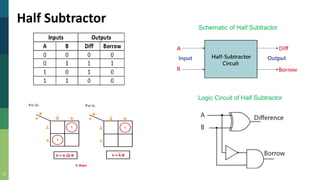
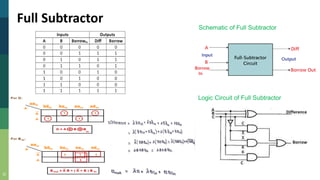
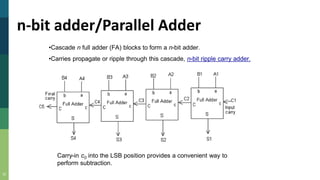
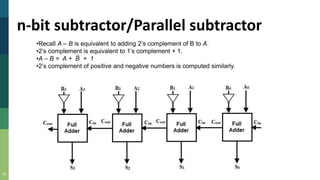
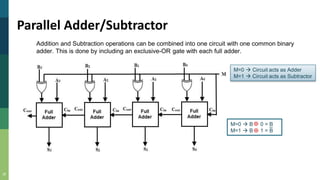
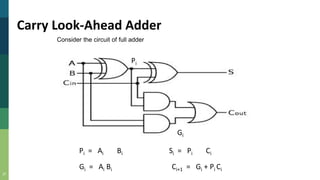
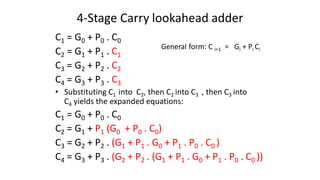
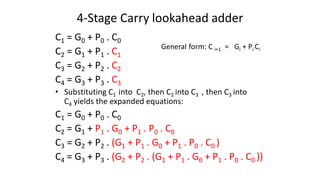
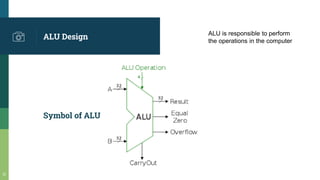
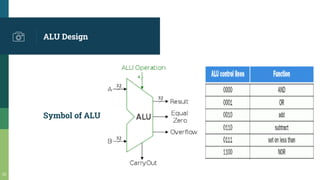
This document discusses combinational and sequential circuits. It begins by defining combinational logic circuits as memoryless digital logic circuits whose output depends only on the current input combination. It then covers various combinational circuits including half adders, full adders, half subtractors, full subtractors, and parallel adders/subtractors. It also discusses sequential circuits including flip-flops and registers. Finally, it covers carry lookahead adders which can speed up the addition process by eliminating inter-stage carry delays.

1. UNIT II
COMBINATIONAL AND SEQUENTIAL CIRCUITS
1
AD8252 - Digital Principles and Computer Organization

2. Syllabus
Combinational circuits – Adder – Subtractor –
ALU Design – Decoder – Encoder –
Multiplexers – Introduction to Sequential
Circuits – Flip-Flops – Registers – Counters.
2

3. Combinational Circuits
Combinational Logic Circuits
are memory less digital logic
circuits whose output at any
instant in time depends only on
the combination of its inputs.
3

4. Adder
4
Rules for binary addition
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 102

5. 5
Half Adder
• The half adder adds two single binary input digits A and B.
• It has two outputs, sum (S) and carry (C).
• The carry signal represents an overflow into the next digit of a multi-digit
addition.
Inputs Outputs
A B Carry Sum
0 0 0 0
1 0 0 1
0 1 0 1
1 1 1 0

6. 6
Half Adder
Inputs Outputs
A B Carry Sum
0 0 0 0
1 0 0 1
0 1 0 1
1 1 1 0
Schematic of Half adder
Logic Circuit of Half adder

7. 7
Full Adder
• A full-adder is a combinational circuit that forms the
arithmetic sum of three input bits
• It consists of 3 inputs and 2 outputs

8. 8
Full Adder

9. 9
Full Adder
Logic Diagram of Full Adder

10. Subtractor
10
Rules for binary subtraction
0 - 0 = 0
0 - 1 = 1 with 1 borrow
1 - 0 = 1
1 - 1 = 0

11. 11
Half Subtractor
Schematic of Half Subtractor
Logic Circuit of Half Subtractor

12. 12
Full Subtractor
Schematic of Full Subtractor
Logic Circuit of Full Subtractor

13. 13
n-bit adder/Parallel Adder
•Cascade n full adder (FA) blocks to form a n-bit adder.
•Carries propagate or ripple through this cascade, n-bit ripple carry adder.
Carry-in c0 into the LSB position provides a convenient way to
perform subtraction.

14. 14
n-bit subtractor/Parallel subtractor
•Recall A – B is equivalent to adding 2’s complement of B to A.
•2’s complement is equivalent to 1’s complement + 1.
•A – B = A + B + 1
•2’s complement of positive and negative numbers is computed similarly.

15. 15
Parallel Adder/Subtractor
Addition and Subtraction operations can be combined into one circuit with one common binary
adder. This is done by including an exclusive-OR gate with each full adder.
M=0  Circuit acts as Adder
M=1  Circuit acts as Subtractor
M=0  B 0 = B
M=1  B 1 = B

16. 16
Drawback
• Sum and carry of any stage cannot be produced until the input carry occurs.
• This leads to a time delay in addition process.
• This delay is known as Carry Propagation Delay.
• One method of speeding up this process by eliminating inter stage carry delay is
called lookahead-carry addition

17. 17
Carry Look-Ahead Adder
Consider the circuit of full adder
Pi
Gi
Pi = Ai Bi Si = Pi Ci
Gi = Ai Bi Ci+1 = Gi + Pi Ci

18. 4-Stage Carry lookahead adder
C1 = G0 + P0 . C0
C2 = G1 + P1 . C1
C3 = G2 + P2 . C2
C4 = G3 + P3 . C3
• Substituting C1 into C2, then C2 into C3 , then C3 into
C4 yields the expanded equations:
C1 = G0 + P0 . C0
C2 = G1 + P1 (G0 + P0 . C0)
C3 = G2 + P2 . (G1 + P1 . G0 + P1 . P0 . C0 )
C4 = G3 + P3 . (G2 + P2 . (G1 + P1 . G0 + P1 . P0 . C0 ))
General form: C i+1 = Gi + Pi Ci

19. 4-Stage Carry lookahead adder
C1 = G0 + P0 . C0
C2 = G1 + P1 . C1
C3 = G2 + P2 . C2
C4 = G3 + P3 . C3
• Substituting C1 into C2, then C2 into C3 , then C3 into
C4 yields the expanded equations:
C1 = G0 + P0 . C0
C2 = G1 + P1 . G0 + P1 . P0 . C0
C3 = G2 + P2 . (G1 + P1 . G0 + P1 . P0 . C0 )
C4 = G3 + P3 . (G2 + P2 . (G1 + P1 . G0 + P1 . P0 . C0 ))
General form: C i+1 = Gi + Pi Ci

20. 4- bit Carry-lookahead adder

21. ALU Design
21
Symbol of ALU
ALU is responsible to perform
the operations in the computer

22. ALU Design
22
Symbol of ALU