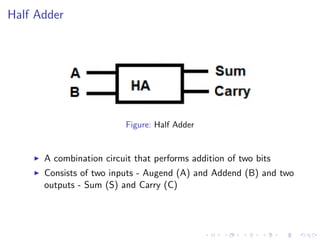
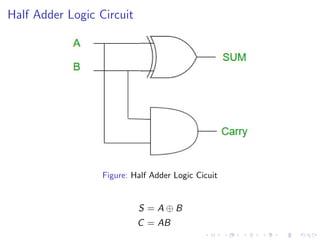
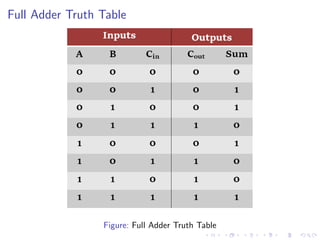
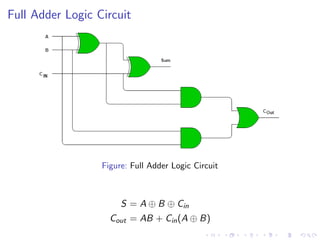
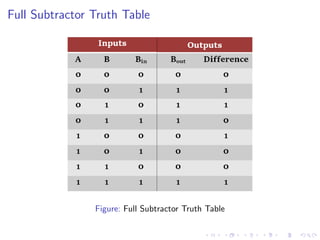
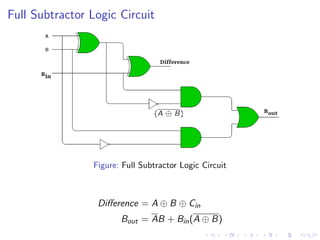
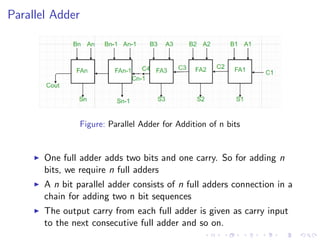
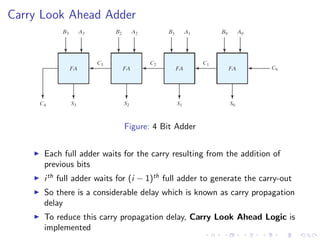
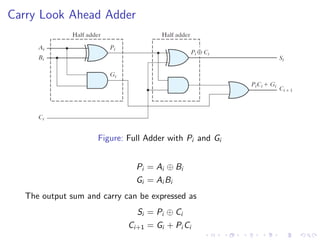
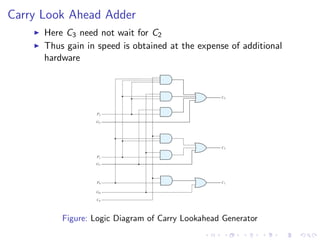
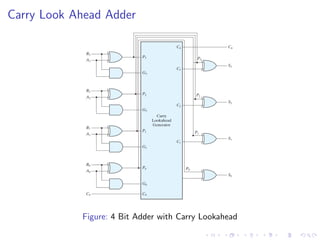
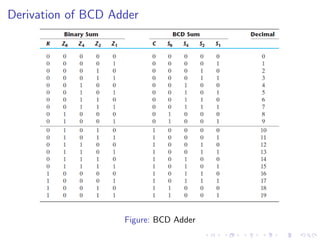
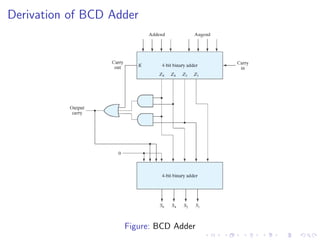
The document describes various binary adders and subtractors used in digital circuits, including half adders, full adders, half subtractors, full subtractors, parallel adders, carry lookahead adders, and BCD adders. It explains their logic functions, truth tables, logic circuits, and implementations. It also provides examples of problems involving calculating propagation delays of ripple carry adders with different bit sizes and gate delays.

1. Binary Adder and Subtractor
Department of Electronics and Communication Engineering,
National Engineering College,
Kovilpatti

2. Table of contents
Binary Adder
Half Adder
Full Adder
Binary Subtractor
Half Subtractor
Full Subtractor
Parallel Adders
Carry Look Ahead Adder
BCD Adder
Problems

3. Half Adder
Figure: Half Adder
I A combination circuit that performs addition of two bits
I Consists of two inputs - Augend (A) and Addend (B) and two
outputs - Sum (S) and Carry (C)

4. Half Adder Truth Table
Figure: Half Adder Truth Table
The corresponding Boolean expressions for Sum and Carry are,
S = AB + AB
= A ⊕ B
C = AB

5. Half Adder Logic Circuit
Figure: Half Adder Logic Cicuit
S = A ⊕ B
C = AB

6. Full Adder
Figure: Full Adder
I A combination circuit that performs addition of three bits
I Consists of three inputs - Augend (A), Addend (B) and
Carry-in (Cin) and two outputs - Sum (S) and Carry-out (Cout)
I The term full adder indicates that it can be implemented
using two half adders

7. Full Adder Truth Table
Figure: Full Adder Truth Table

8. Simplified expression for Sum and Carryout
Figure: Karnaugh maps for Sum and Carry-out
The corresponding Boolean expressions for Sum and Carry-in are obtained as
S = ABCin + ABCin + ABCin + ABCin
= Cin(AB + AB) + Cin(AB + AB)
= Cin(A ⊕ B) + Cin(A ⊕ B)
= Cin ⊕ A ⊕ B
Cout = AB + BCin + ACin
= AB + BCin(A + A) + ACin(B + B)
= AB + ABCin + ABCin + ABCin + ABCin
= AB(1 + Cin) + Cin(AB + AB)
= AB + Cin(A ⊕ B)

9. Full Adder Logic Circuit
Figure: Full Adder Logic Circuit
S = A ⊕ B ⊕ Cin
Cout = AB + Cin(A ⊕ B)

10. Full Adder Using Two Half Adders
Figure: Full Adder using two half adders

11. Half Subtractor
Figure: Half Subtractor
I A combination circuit that performs subtraction of two bits
I Consists of two inputs - Minuend (A) and Subtrahend (B) and
two outputs - Difference and Borrow

12. Half Subtractor Truth Table
Figure: Half Subtractor Truth Table
The corresponding Boolean expressions for Difference and Borrow
are,
Difference = AB + AB
= A ⊕ B
Borrow = AB

13. Half Subtractor Logic Circuit
Figure: Half subtractor Logic Cicuit
Difference = A ⊕ B
Borrow = AB

14. Full Subtractor
Figure: Full Subtractor
I A combination circuit that performs addition of three bits
I Consists of three inputs - Minuend (A), Subtrahend (B) and
Borrow-in (Bin) and two outputs - Difference (D) and
Borrow-out (Bout)

15. Full Subtractor
Consider the example, (010)2 - (001)2

16. Full Subtractor Truth Table
Figure: Full Subtractor Truth Table

17. Simplified expression for Difference and Borrowout
Figure: Karnaugh maps for Difference and Borrowout
The corresponding Boolean expressions for Difference and Borrowout are obtained as
D = ABBin + ABBin + ABBin + ABBin
= Bin(AB + AB) + Bin(AB + AC)
= Bin(A ⊕ B) + Bin(A ⊕ B)
= Bin ⊕ A ⊕ B
Bout = AB + ABin + BBin
= AB + ABin(B + B) + BBin(A + A)
= AB + ABBin + ABBin + ABBin + ABBin
= AB(1 + Bin) + Bin(AB + AB)
= AB + Bin(A ⊕ B)

18. Full Subtractor Logic Circuit
Figure: Full Subtractor Logic Circuit
Difference = A ⊕ B ⊕ Cin
Bout = AB + Bin(A ⊕ B)

19. Parallel Adder
Figure: Parallel Adder for Addition of n bits
I One full adder adds two bits and one carry. So for adding n
bits, we require n full adders
I A n bit parallel adder consists of n full adders connection in a
chain for adding two n bit sequences
I The output carry from each full adder is given as carry input
to the next consecutive full adder and so on.

20. Carry Look Ahead Adder
Figure: 4 Bit Adder
I Each full adder waits for the carry resulting from the addition of
previous bits
I ith
full adder waits for (i − 1)th
full adder to generate the carry-out
I So there is a considerable delay which is known as carry propagation
delay
I To reduce this carry propagation delay, Carry Look Ahead Logic is
implemented

21. Carry Look Ahead Adder
Figure: Full Adder with Pi and Gi
Pi = Ai ⊕ Bi
Gi = Ai Bi
The output sum and carry can be expressed as
Si = Pi ⊕ Ci
Ci+1 = Gi + Pi Ci

22. Carry Look Ahead Adder
I Gi is Carry Generate and it produces a carry of 1 if both Ai
and Bi are 1, regardless of Ci
I Pi is Carry Propagate, because it determines whether a carry
from stagei will propagate to stagei+1
I Boolean function for each output carry is given as
C0 = inputcarry
C1 = G0 + P0C0
C2 = G1 + P1C1
= G1 + P1(G0 + P0C0)
= G1 + P1G0 + P1P0C0
C3 = G2 + P2C2
= G2 + P2(G1 + P1G0 + P1P0C0)
= G2 + P2G1 + P2P1G0 + P2P1P0C0

23. Carry Look Ahead Adder
I Here C3 need not wait for C2
I Thus gain in speed is obtained at the expense of additional
hardware
Figure: Logic Diagram of Carry Lookahead Generator

24. Carry Look Ahead Adder
Figure: 4 Bit Adder with Carry Lookahead

25. Derivation of BCD Adder
Figure: BCD Adder

26. Derivation of BCD Adder
I When the binary sum exceeds 1001, 0110 is added to make it
a valid BCD sum
I From the table, it is observed that correction is added when
i Output carry K = 1
ii Other six combinations have 1 in Z8 and either Z4 & Z2
C = K + Z8Z4 + Z8Z2
I So, if C = 1, 0110 is added to the sum.

27. Derivation of BCD Adder
Figure: BCD Adder

28. Problem 1
[GATE-CS-2015] A half adder is implemented with XOR and AND
gates. A full adder is implemented with two half adders and one
OR gate. The propagation delay of an XOR gate is twice that of
an AND/OR gate. The propagation delay of an AND/OR gate is
1.2 microseconds. A 4-bit ripple-carry binary adder is implemented
by using full adders. The total propagation time of this 4-bit
binary adder in microseconds is

29. Problem 1
[GATE-CS-2015] A half adder is implemented with XOR and AND
gates. A full adder is implemented with two half adders and one
OR gate. The propagation delay of an XOR gate is twice that of
an AND/OR gate. The propagation delay of an AND/OR gate is
1.2 microseconds. A 4-bit ripple-carry binary adder is implemented
by using full adders. The total propagation time of this 4-bit
binary adder in microseconds is

30. Solution GATE-CS-2015
I Full adder consists of 2 XOR, 2 AND and 1 OR gates
I The worst case propagation delay is then,
i 4 gate-delays from generating the first carry signal (A0/B0
C1).
ii 2 gate-delays per intermediate stage (Ci Ci+1).
iii 2 gate-delays at the last stage to produce both the sum and
carry-out outputs (Cn-1 Cn and Sn-1).
I Hence the total propagation delay for a n-bit full adder is,
tp = 4 + 2(n − 2) + 2
= 2n + 2

31. Solution GATE-CS-2015
A half adder is implemented with XOR and AND gates. A full
adder is implemented with two half adders and one OR gate. The
propagation delay of an XOR gate is twice that of an AND/OR
gate. The propagation delay of an AND/OR gate is 1.2
microseconds. A 4-bit ripple-carry binary adder is implemented by
using full adders. The total propagation time of this 4-bit binary
adder in microseconds is

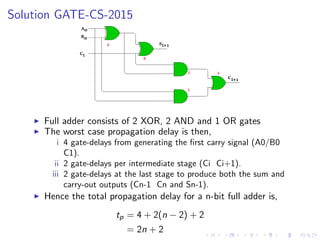
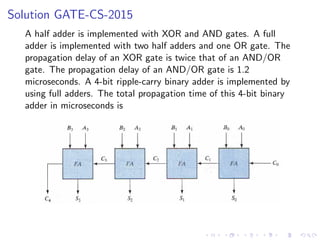
32. Solution GATE-CS-2015
A half adder is implemented with XOR and AND gates. A full
adder is implemented with two half adders and one OR gate. The
propagation delay of an XOR gate is twice that of an AND/OR
gate. The propagation delay of an AND/OR gate is 1.2
microseconds. A 4-bit ripple-carry binary adder is implemented by
using full adders. The total propagation time of this 4-bit binary
adder in microseconds is
Answer: 4[(2n+2)*1.2] = 19.2ms

33. Problem 2
[GATE-EC-2017] Figure I shows a 4-bit ripple carry adder realized using
full adders and Figure II shows the circuit of a full-adder (FA). The
propagation delay of the XOR, AND and OR gates in Figure II are 20 ns,
15 ns and 10 ns, respectively. Assume all the inputs to the 4-bit adder
are initially reset to 0.
At t = 0, the input to the 4-bit adder are changed to A3A2A1A0 = 1100,
B3B2B1B0 = 0100 and C0 = 1. The output of the ripple carry adder will
be stable at t (in ns)=

34. Problem 2
[GATE-EC-2017] Figure I shows a 4-bit ripple carry adder realized using
full adders and Figure II shows the circuit of a full-adder (FA). The
propagation delay of the XOR, AND and OR gates in Figure II are 20 ns,
15 ns and 10 ns, respectively. Assume all the inputs to the 4-bit adder
are initially reset to 0.
At t = 0, the input to the 4-bit adder are changed to A3A2A1A0 = 1100,
B3B2B1B0 = 0100 and C0 = 1. The output of the ripple carry adder will
be stable at t (in ns)=
Solution: Link

35. Problem 3
[GATE ECE 2014 Set 4] A 16-bit ripple carry adder is realized
using 16 identical full adders (FA) as shown in the figure. The
carry-propagation delay of each FA is 12 ns and the sum
propagation delay of each FA is 15 ns. The worst case delay (in ns)
of this 16-bit adder will be

36. Problem 3
[GATE ECE 2014 Set 4] A 16-bit ripple carry adder is realized
using 16 identical full adders (FA) as shown in the figure. The
carry-propagation delay of each FA is 12 ns and the sum
propagation delay of each FA is 15 ns. The worst case delay (in ns)
of this 16-bit adder will be
Answer: For the 1st FA, the carry propagation delay is 12 ns. So
the 2nd FA will generate its carry after 24ns. Therefore, the worst
case delay is = (15*12) + 15 = 195 ns

37. Thank You