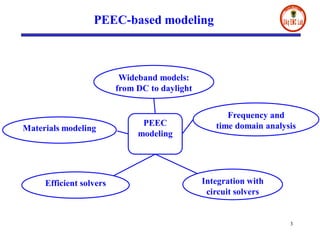
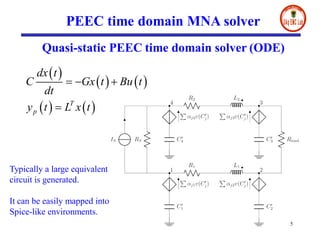
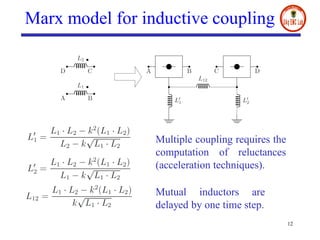
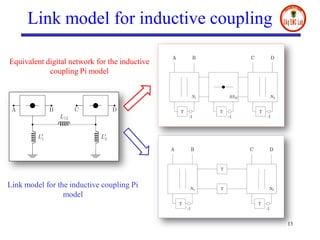
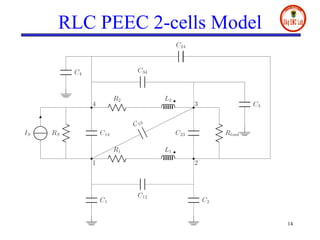
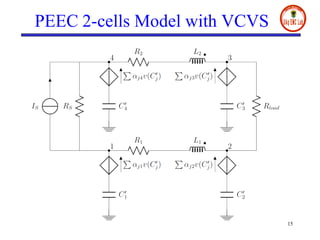
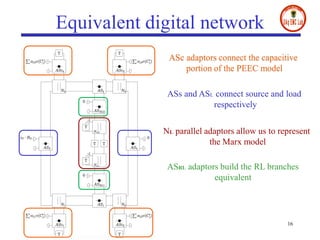
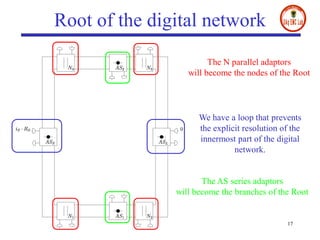
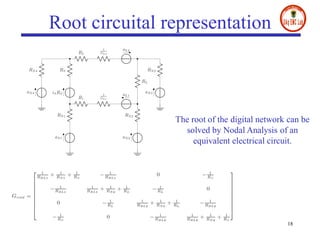
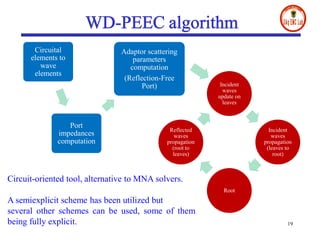
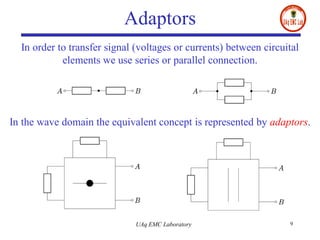
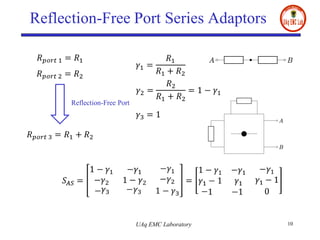
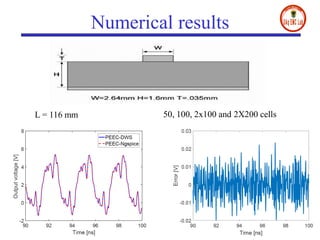
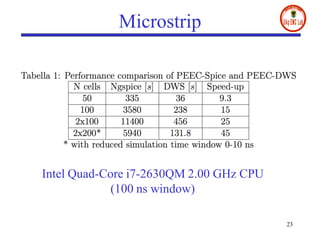
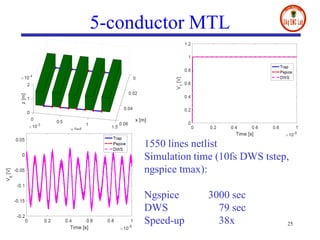
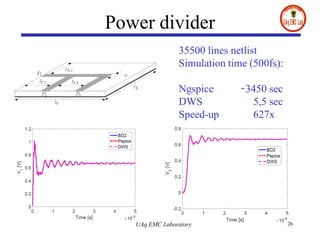
- The document presents a digital wave formulation of the partial element equivalent circuit (PEEC) method for quasi-static electromagnetic problems. - It converts traditional PEEC networks into an equivalent digital wave network using scattering parameters and reflection-free ports. This allows for a more explicit solution scheme compared to matrix node analysis approaches. - Numerical results on microstrip and multilayer structures show significant speed-ups of up to 627 times compared to traditional SPICE solvers when using the proposed digital wave PEEC approach.

1. Digital Wave Formulation of Quasi-Static
Partial Element Equivalent Circuit Method
Piero Belforte, Luigi Lombardi,
Daniele Romano, Giulio Antonini
piero.belforte@gmail.com , luigilombardi89@gmail.com,
daniele.romano.vis@gmail.com, giulio.antonini@univaq.it,
SPI 2016
Torino, May 10, 2016

2. Summary
o Basic PEEC theory
o Digital Wave Networks
o Digital Wave PEEC Network
o Solution algorithm
o Digital Wave Simulator
o Numerical results
o Conclusions
2

3. 3
PEEC-based modeling
PEEC
modeling
Materials modeling
Frequency and
time domain analysis
Integration with
circuit solvers
Wideband models:
from DC to daylight
Efficient solvers

4. Basic PEEC Theory
Invented by A. Ruehli (IBM) through the concepts of
 partial inductance (1972)
 partial capacitance (1973)
 integrating them into the same formulation (1974)
4

5. PEEC time domain MNA solver
Quasi-static PEEC time domain solver (ODE)
 
   
   T
p
dx t
C Gx t Bu t
dt
y t L x t
  

5
Typically a large equivalent
circuit is generated.
It can be easily mapped into
Spice-like environments.

6. Digital wave network (DWN)
6
• PEEC model analysis are tipically performed in
current and voltage (or sometimes charge) variables.
• A possible alternative approach can use incident and
reflected voltage wave variables.
DWN is not just a change of variables !!!

7. 7
Continuous to discrete time transform
Bilinear transform Trapezoidal rule
Inductance
The computation of the reflected wave for the next time
step is completely explicit !!!

8. 8
Continuous to discrete time transform
Capacitance:
Resistance:
Analogously ...
• Constitutive equations are explicit!!
• … nevertheless Kirchoff laws still enforce implicit
equations…
• ... we can get a more explicit scheme by introducing
delays on coupling modeling.

9. Adaptors
UAq EMC Laboratory 9
In order to transfer signal (voltages or currents) between circuital
elements we use series or parallel connection.
In the wave domain the equivalent concept is represented by adaptors.

10. Reflection-Free Port Series Adaptors
UAq EMC Laboratory 10
Reflection-Free Port

11. Reflection-Free Port Parallel Adaptors
UAq EMC Laboratory 11
Reflection-Free Port

12. Marx model for inductive coupling
12
Multiple coupling requires the
computation of reluctances
(acceleration techniques).
Mutual inductors are
delayed by one time step.

13. Link model for inductive coupling
13
Equivalent digital network for the inductive
coupling Pi model
Link model for the inductive coupling Pi
model

14. RLC PEEC 2-cells Model
14

15. PEEC 2-cells Model with VCVS
15

16. Equivalent digital network
16
ASc adaptors connect the capacitive
portion of the PEEC model
ASs and ASL connect source and load
respectively
NL parallel adaptors allow us to represent
the Marx model
ASRL adaptors build the RL branches
equivalent

17. 17
Root of the digital network
The N parallel adaptors
will become the nodes of the Root
The AS series adaptors
will become the branches of the Root
We have a loop that prevents
the explicit resolution of the
innermost part of the digital
network.

18. Root circuital representation
18
The root of the digital network can be
solved by Nodal Analysis of an
equivalent electrical circuit.

19. 19
Incident
waves
update on
leaves
Incident
waves
propagation
(leaves to
root)
Root
Reflected
waves
propagation
(root to
leaves)
Circuital
elements to
wave
elements
Port
impedances
computation
Adaptor scattering
parameters
computation
(Reflection-Free
Port)
Circuit-oriented tool, alternative to MNA solvers.
A semiexplicit scheme has been utilized but
several other schemes can be used, some of them
being fully explicit.

20. Digital Wave Simulator (DWS)
• Development started at CSELT Labs (Turin) in 1974 by P. Belforte & G.
Guaschino for design of high-speed digital systems
• From 1986 to 2001 at HDT (Turin) as general purpose Spice-like simulator
(SPRINT). SI/PI/EMC applications included PRESTO (post-layout),
EMIR (emissions) and THRIS in cooperation with CSELT (Qualification
tool)
• In 1998 at HDT first DWS-PEEC application (3D_PEEC)
• From 2001 to present as DWS including Multi-gigabit applications as
HiSAFE for Cisco Systems (P. Belforte)
• From 2012 also as Spicy SWAN cloud-based app
• From Feb. 2016 new PEEC-DWS developments in a cooperation driven by
P.Belforte and G.Antonini.
20

21. DWS early applications (1975)
UAq EMC Laboratory 21
CSELT LABS: ETA (Easy Transient Analysis) application to the design of a .5Gbps
high-speed Multichip Module. A TDR-based wideband measurement system was
included in the Digital Wave modeling & simulation environment.

22. DWS main features
• Conversion of a Spice-like netlist into a Digital Network
equivalent including circuital elements and nodes as
scattering blocks exchanging waves at their ports.
• DSP oriented solution apart from the root. DFLs solved by
port-matching calculation scheduling
• Wideband SI/PI/EMC applications
• Complementary to Spice
Detailed documents available at
https://www.researchgate.net/profile/Piero_Belforte
22

23. Numerical results
23
L = 116 mm 50, 100, 2x100 and 2X200 cells

24. Microstrip
Intel Quad-Core i7-2630QM 2.00 GHz CPU
(100 ns window)
23

25. 5-conductor MTL
25
1550 lines netlist
Simulation time (10fs DWS tstep,
ngspice tmax):
Ngspice 3000 sec
DWS 79 sec
Speed-up 38x

26. Power divider
UAq EMC Laboratory 26
35500 lines netlist
Simulation time (500fs):
Ngspice ̴ 3450 sec
DWS 5,5 sec
Speed-up 627x

27. Conclusions
27
• A Digital Wave (DW) model of quasi-static PEEC circuits has
been proposed.
• A proper scheduling of calculations has been used.
• Significant speed-ups (up to 627x) have been experienced
replacing MNA Spice-like solvers with DWS.
• DWS speed-up increases with PEEC model complexity.
• A semi-explicit scheme has been tested so far but...
• ...at least 7 more implementations including fully explicit schemes
with different stability properties and performances are possible.
They are under investigation.

28. Future work
UAq EMC Laboratory 28
• Inclusion of physical delays leading also to a fully
explicit scheme.
• Stability and passivity analysis of delayed wave digital
network.
• Developement of a in-house Digital Wave PEEC Solver
exploiting the features of all the possible topologies.
• Inclusion of skin-effect and dielectric losses.

29. UAq EMC Laboratory 29
Thank you for your attention !