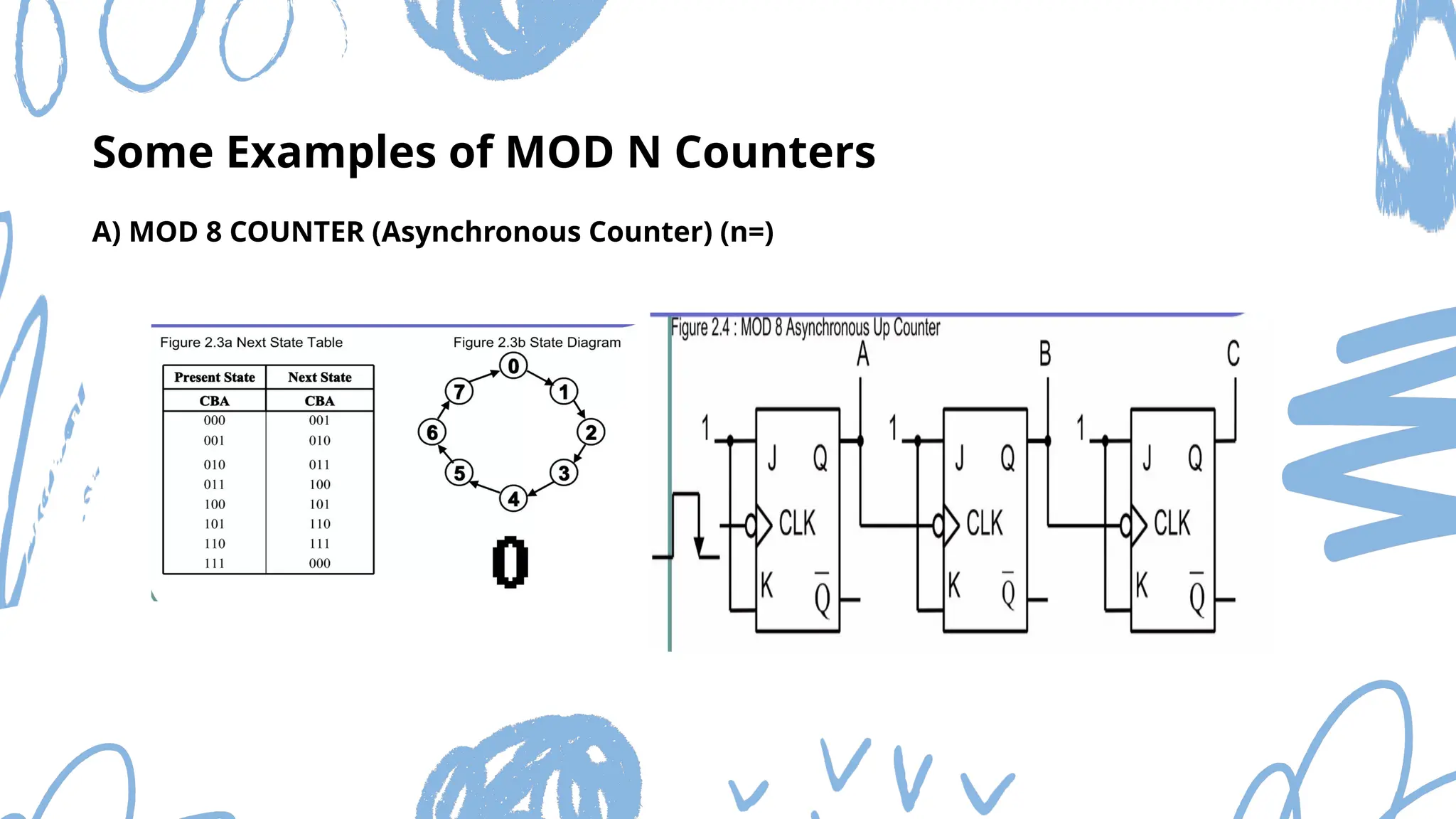
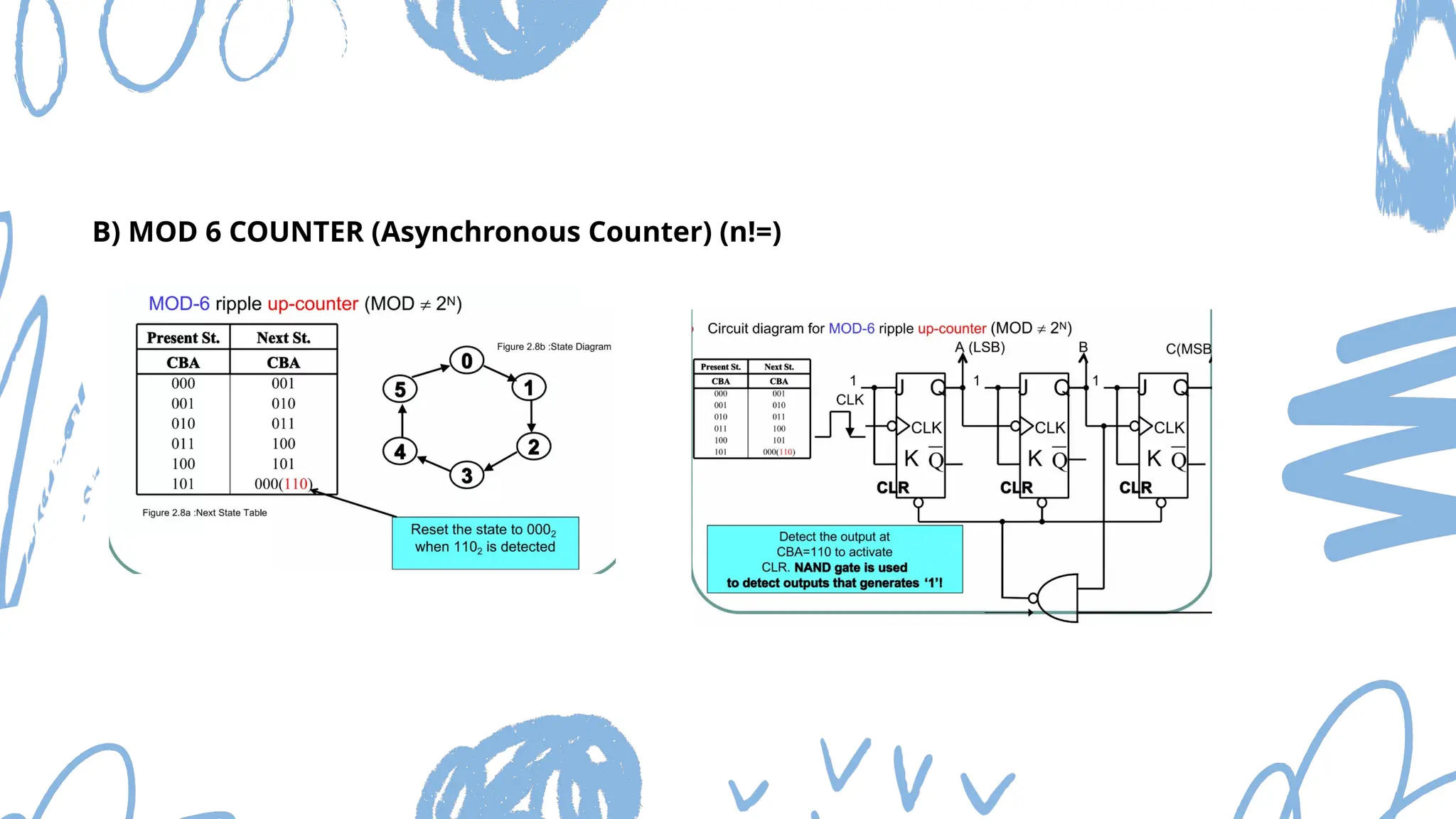
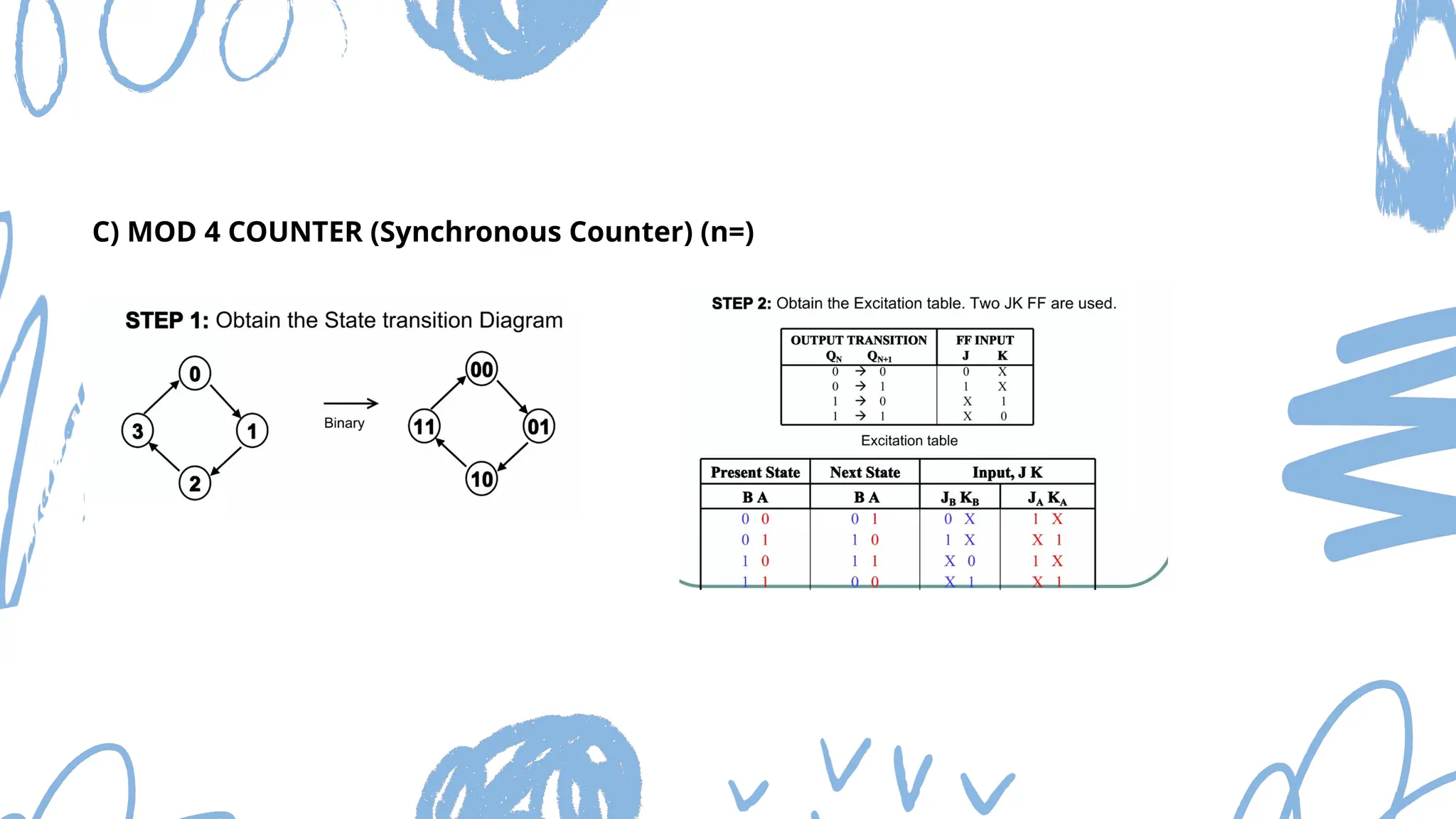
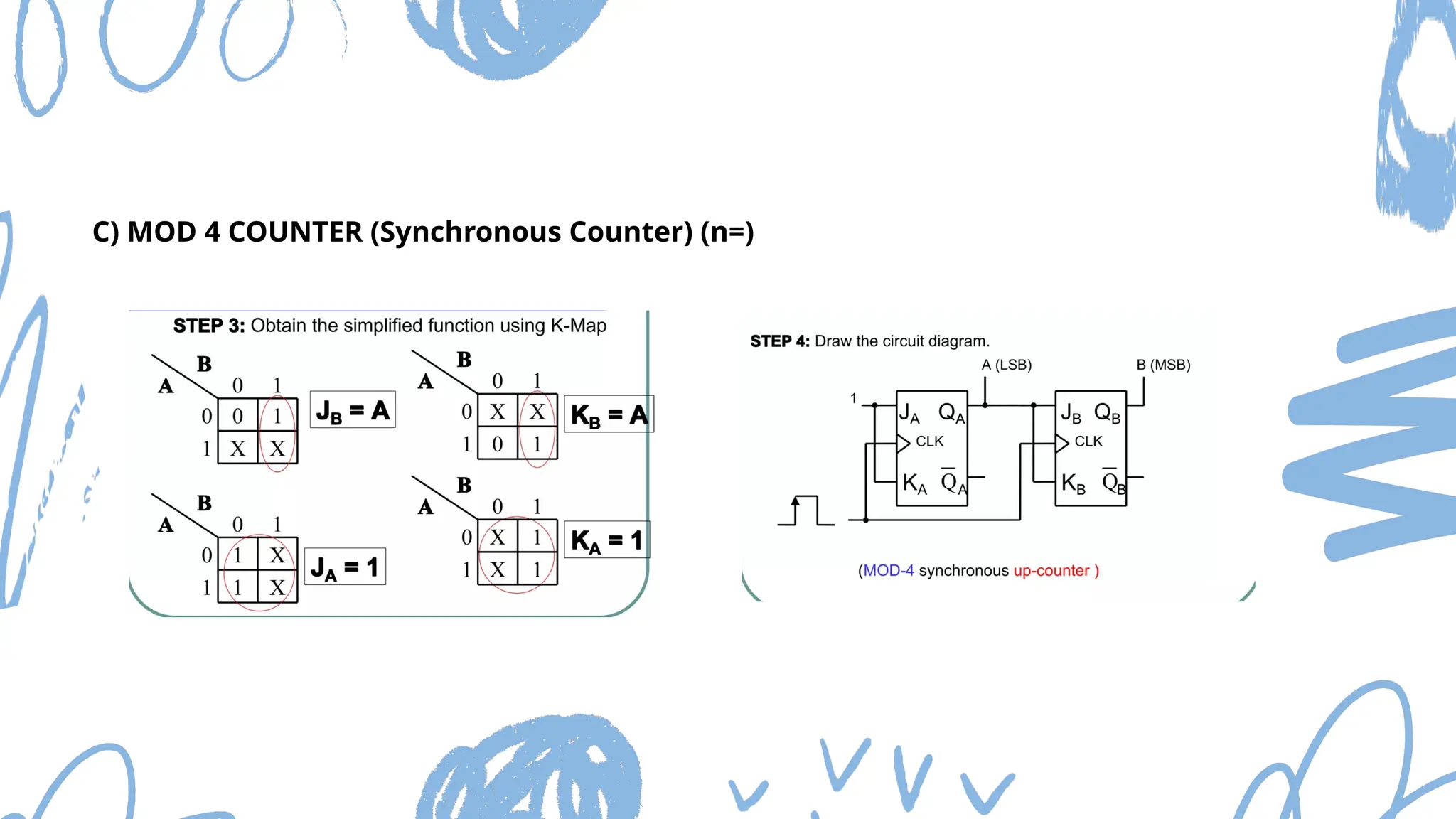
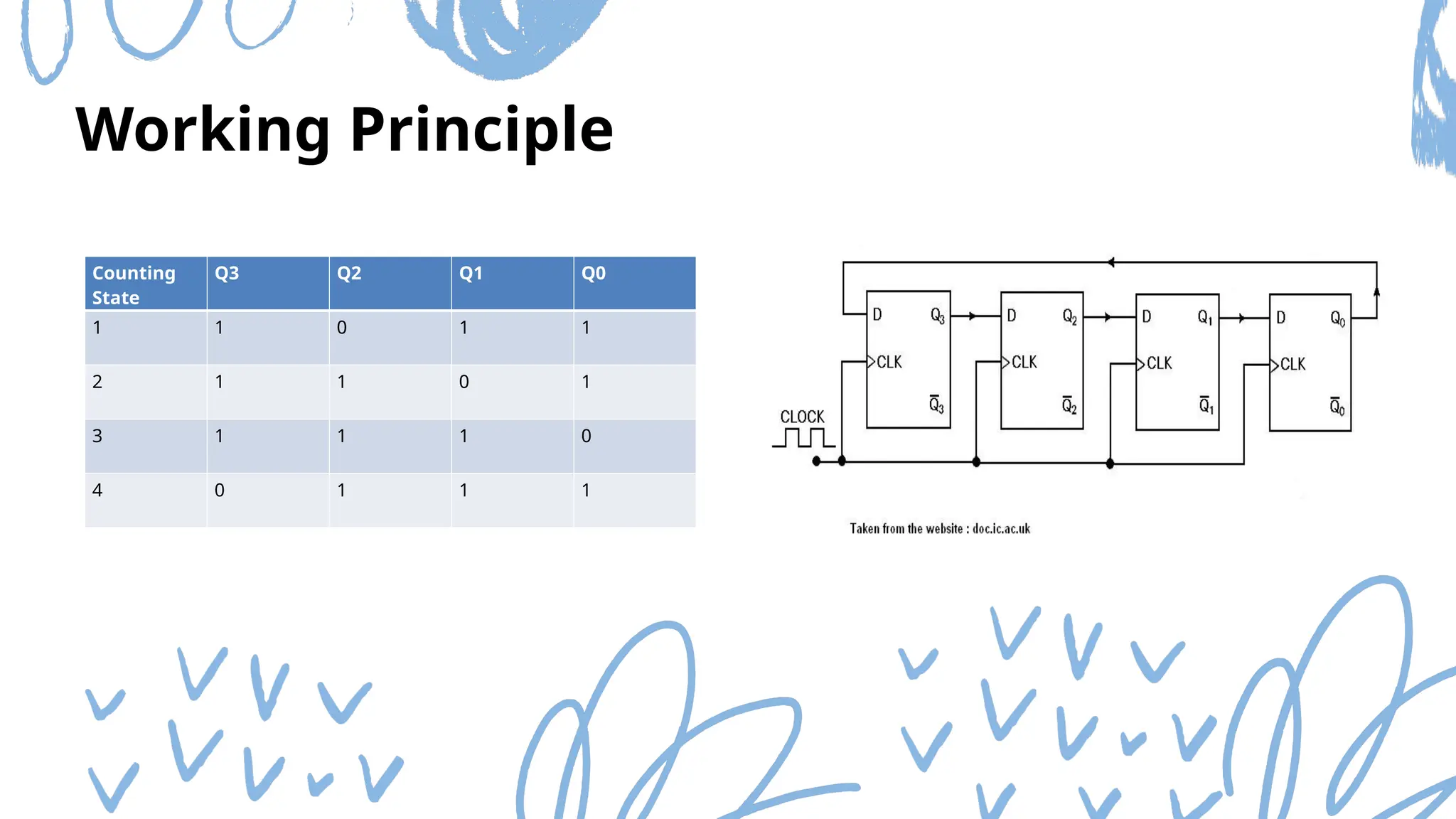
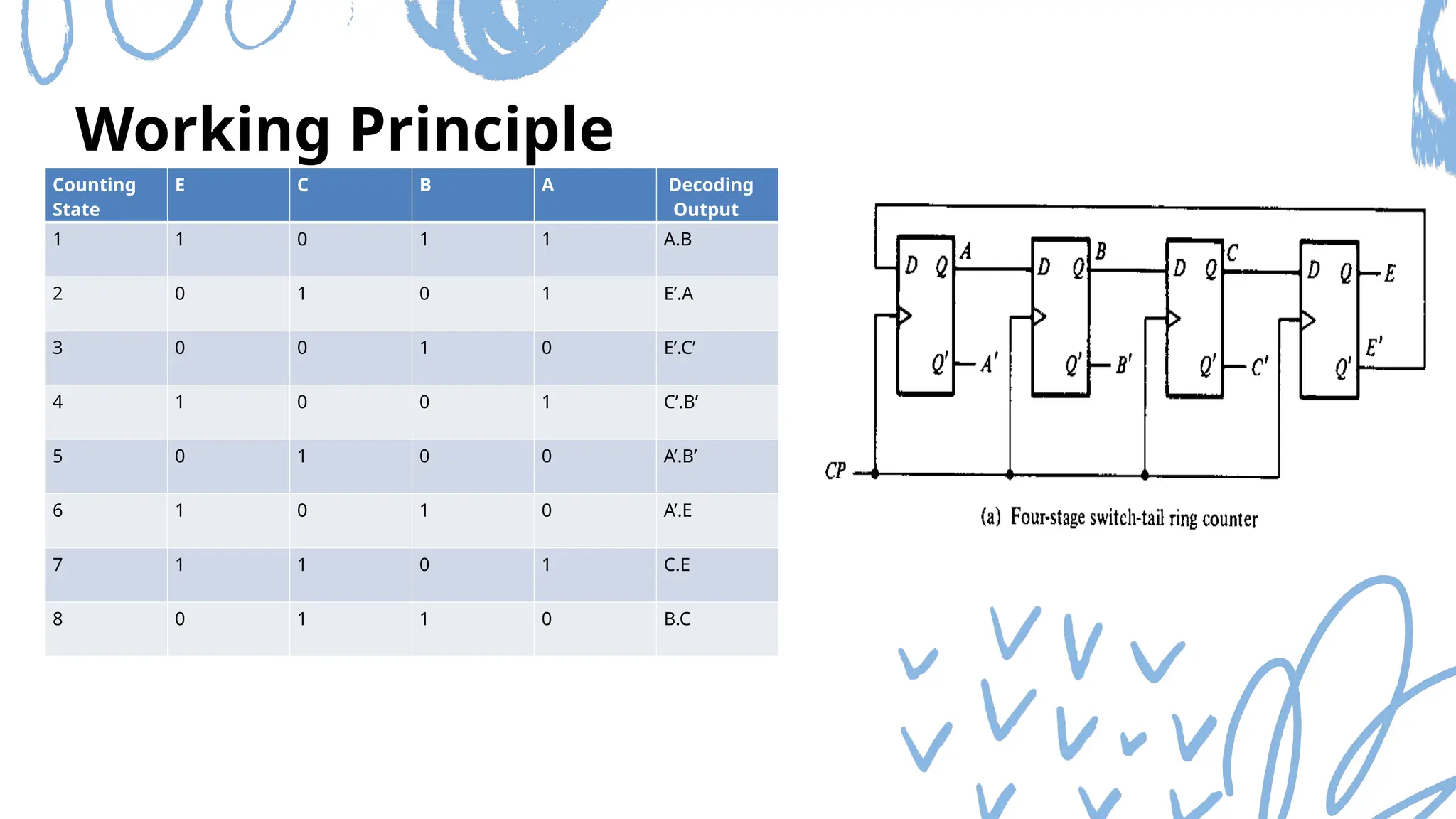
The document discusses Mod n counters, Ring counters, and Johnson counters, detailing their definitions, principles, and applications. Mod n counters utilize flip-flops to count through states, while Ring and Johnson counters are synchronous counters based on shift registers. Various examples and applications for these counters are illustrated, highlighting their importance in digital electronics.

1. MOD N COUNTERS
&
JOHNSON COUNTERS
Samir Poudel
Sanjana Shrestha
Shishir Ghimire
Srijana Devkota
Presented By:

2. CONTENTS
01 02
MOD N COUNTERS RING COUNTERS
03
JOHNSON COUNTERS

3. MOD N Counter

4. Introduction
• A circuit which passes through N number of states before returning to the starting
state.
• Simply it can be say that a binary counter counts 0 to N-1.
• For eg : In mod-11 counter it can count 0 to 10 which can be simply say that this
counter has 11 states.
• For MOD N counter, the number of flipflop required by calculating this eqn:N<=
Where ,
n= number of flipflop required
N= integer value written after MOD

5.  For eg : In mod 5 counter :
5<= 5<=8
So , we need 3 flipflops to design mod 5 counter which counts 0 to 4 ie: 5 states
which have 3 bits of number.
 But in some cases n bit = mod counters.
For eg: 3 bit = mod 8 counters. ( ie: =8).
Introduction

6.  No of states through counter passes.
 Decide no of bits for Ripple Counter.
 State Diagram
 Truth Table for analysis.
 Excitation Table for Design
 K Map for Simplification
 Logic Diagram
Steps for Designing MOD N
Counter

7. Some Examples of MOD N Counters
A) MOD 8 COUNTER (Asynchronous Counter) (n=)

8. B) MOD 6 COUNTER (Asynchronous Counter) (n!=)

9. C) MOD 4 COUNTER (Synchronous Counter) (n=)

10. C) MOD 4 COUNTER (Synchronous Counter) (n=)

11.  Time Measurement
 Alarm Clock
 Set a timer for taking the photo in camera.
 Flashing indicator lights in vehicles.
 Digital Clock.
Applications of MOD N counter

12. Ring Counter

13. Introduction
• Digital sequential logic circuit that can be used to count the number of events or
pulses that occur in a system.
• Type of Synchronous Counter ( which same clock pulse is applied to all flip flop) .
• Made up of D flipflop .
• Works on the principle of Shift Register.
• Here K bit of flip flop then k times state of output.
• A type of counter which ring is formed by connecting Q of LSB to D of MSB.

14. Working Principle
 Let us consider the initial binary number be 1011 which is also called as the counting state at 1, where
Q3=1 , Q2=0, Q1=1 and Q0=1.
 Since the given binary number is 4 bit so we use 4 D flipflops which is labelled as Q0, Q1 Q2, Q3.
 Let Q0 flipflop be the LSB and Q3 flipflop be MSB.
 Here, Q3 flipflop is connected to Q2, Q2 connected to Q1 and Q1 is connected to Q0 flipflop.
 Then, in this flipflop Q of Q0 is connected to the flipflop Q3 to form a complete ring counter.
 Let CLK be the clock which is provided to the all 4 flipflop which can be positive or negative triggered which is
applied simultaneously.

15. Working Principle
Counting
State
Q3 Q2 Q1 Q0
1 1 0 1 1
2 1 1 0 1
3 1 1 1 0
4 0 1 1 1

16. Johnson
Counter

17. Introduction
• Digital sequential logic circuit that can be used to count the number of events or
pulses that occur in a system.
• Also called as the Switch Tail Ring Counter.
• Type of Synchronous Counter ( which same clock pulse is applied to all flip flop) .
• Made up of D flipflop .
• Works on the principle of Shift Register.
• A type of ring counter which ring is formed by connecting Q’ of LSB to D of MSB.
• Here K bit of flip flop then 2k times state of output.

18. Working Principle
 Let us consider the initial binary number be 1011 which is also called as the counting state at 1
where E=1 , C=0, B=1 and A=1.
 Since the given binary number is 4 bit so we use 4 D flipflops which is labelled as A B C E.
 Let E flipflop be the LSB and A flipflop be MSB.
 Here A flipflop is connected to B, B connected to C and C is connected to E flipflop.
 Then, in this flipflop Q’ of E is connected to the flipflop A to form a complete ring counter.
 Let CP be the clock which is provided to the all 4 flipflop which can be positive or negative triggered which is applied
simultaneously.

19. Working Principle
Counting
State
E C B A Decoding
Output
1 1 0 1 1 A.B
2 0 1 0 1 E’.A
3 0 0 1 0 E’.C’
4 1 0 0 1 C’.B’
5 0 1 0 0 A’.B’
6 1 0 1 0 A’.E
7 1 1 0 1 C.E
8 0 1 1 0 B.C

20. Applications
 It is used in walking LED.
 It is used to convert the square waves to sine waves

21. Any
Queries?

22. Thank you
very much!