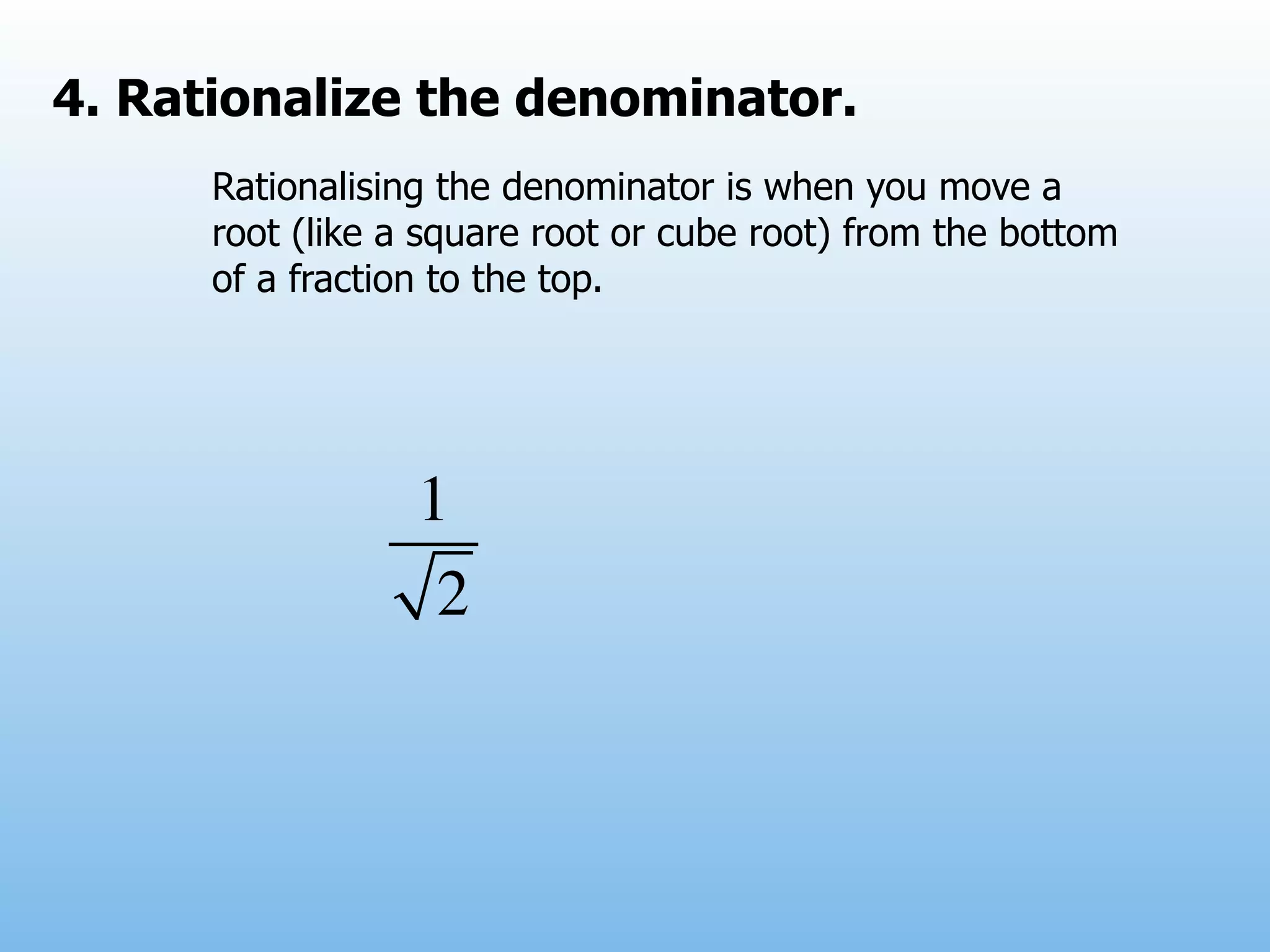
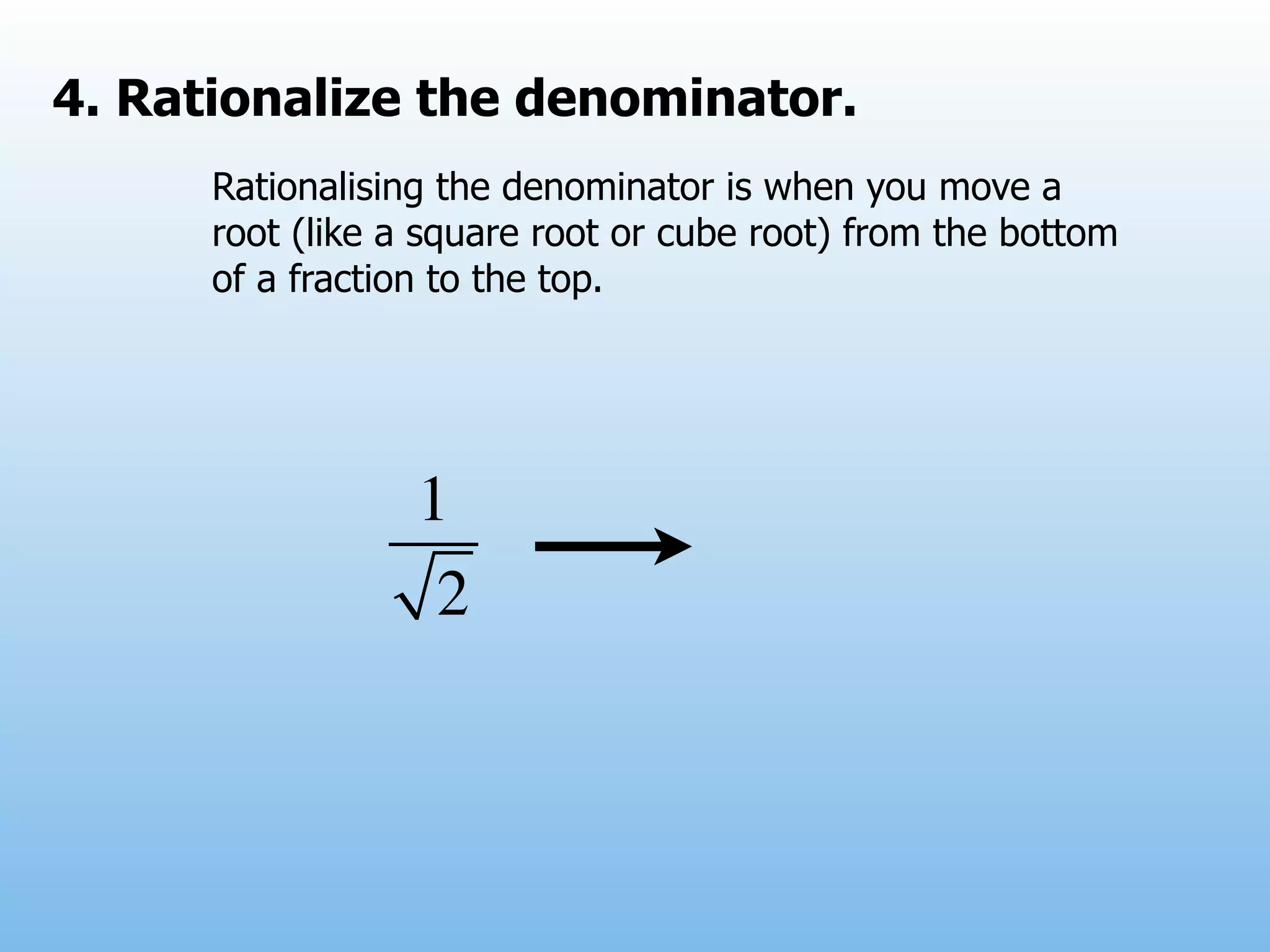
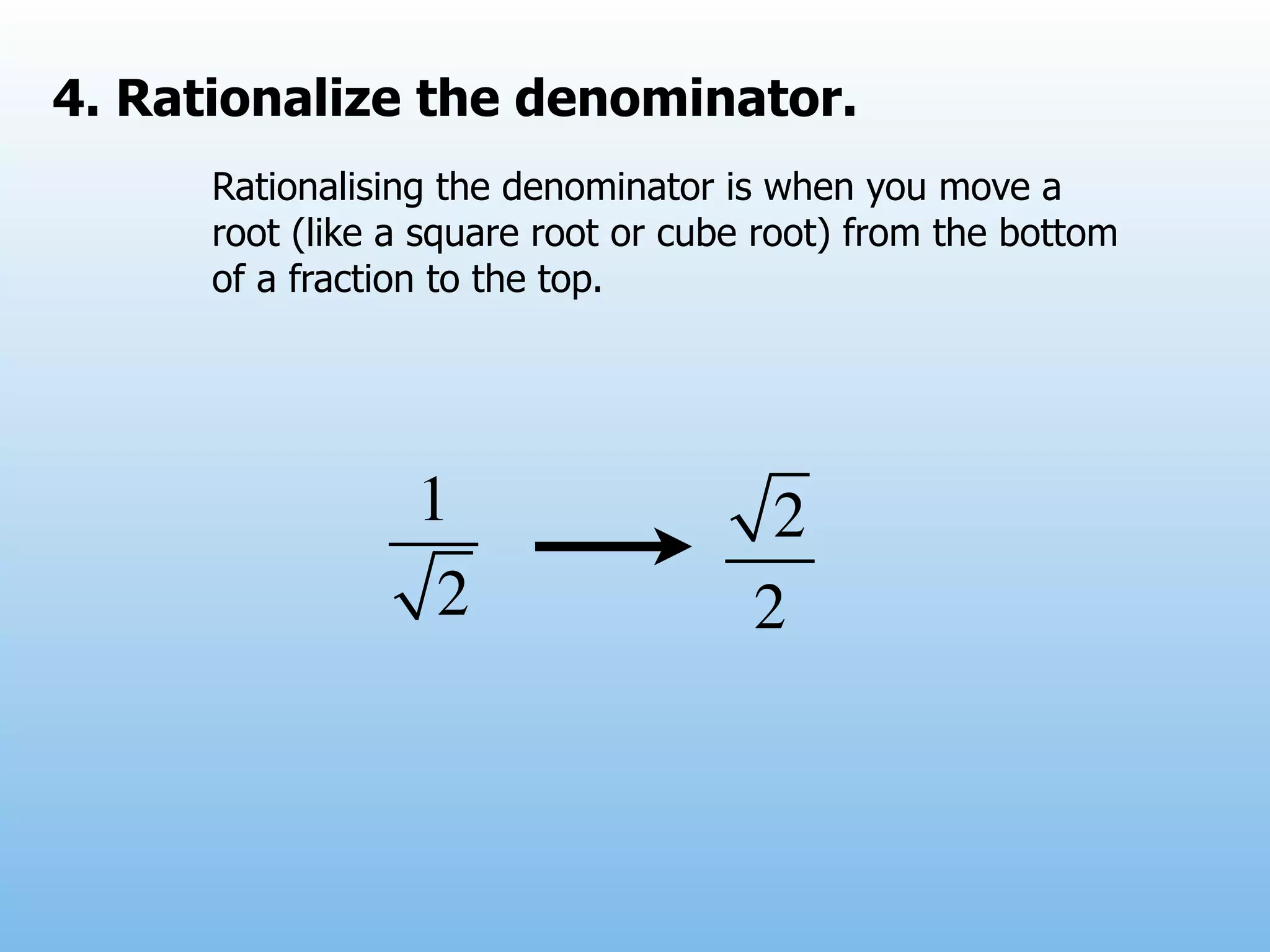
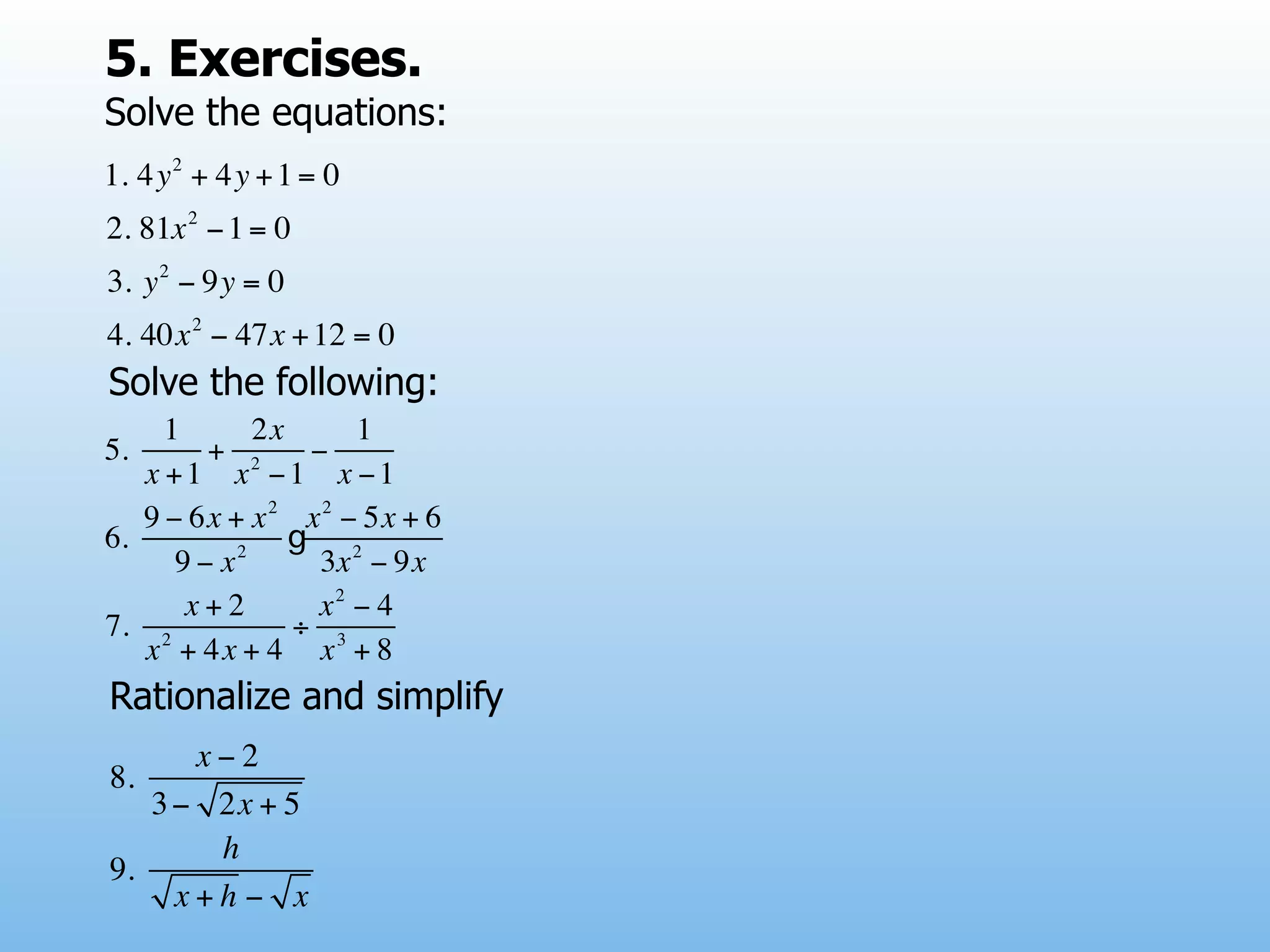The document provides examples and explanations of operations with fractions, including adding, subtracting, multiplying, and dividing fractions. It also explains how to rationalize the denominator of a fraction by moving a root from the bottom of a fraction to the top. Some examples of rationalizing denominators are shown. Finally, it lists some exercises involving solving equations, rationalizing denominators, and performing operations with fractions.

1. 3. Operations with fractions.
Examples:
2 2
1 1 a +b
a) 2 + − 3 3
a − ab ab a b − ab

2. 3. Operations with fractions.
Examples:
2 2
1 1 a +b
a) 2 + − 3 3
a − ab ab a b − ab
2 2
a − 3 a + 9a + 20 a − 16
b) × 2 ÷ 2
4a − 4 a − 6a + 9 2a − 2a

3. 4. Rationalize the denominator.

4. 4. Rationalize the denominator.
Rationalising the denominator is when you move a
root (like a square root or cube root) from the bottom
of a fraction to the top.

5. 4. Rationalize the denominator.
Rationalising the denominator is when you move a
root (like a square root or cube root) from the bottom
of a fraction to the top.
1
2

6. 4. Rationalize the denominator.
Rationalising the denominator is when you move a
root (like a square root or cube root) from the bottom
of a fraction to the top.
1
2

7. 4. Rationalize the denominator.
Rationalising the denominator is when you move a
root (like a square root or cube root) from the bottom
of a fraction to the top.
1 2
2 2

8. 4. Rationalize the denominator.
Examples:
Rationalize the denominator of
2+ 3
8− 3

9. 4. Rationalize the denominator.
Examples:
Rationalize the denominator of
2+ 3
8− 3
Rationalize and simplify

10. 4. Rationalize the denominator.
Examples:
Rationalize the denominator of
2+ 3
8− 3
Rationalize and simplify
a +1
1+ a + 1

11. 5. Exercises.
Solve the equations:
1. 4y 2 + 4y + 1 = 0
2. 81x 2 − 1 = 0
3. y 2 − 9y = 0
4. 40x 2 − 47x + 12 = 0
Solve the following:
1 2x 1
5. + 2 −
x +1 x −1 x −1
9 − 6x + x 2 x 2 − 5x + 6
6. 2
g 2
9− x 3x − 9x
x+2 x2 − 4
7. 2 ÷
x + 4x + 4 x 3 + 8
Rationalize and simplify
x−2
8.
3 − 2x + 5
h
9.
x+h − x