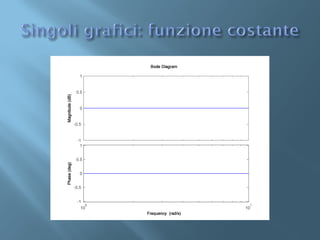
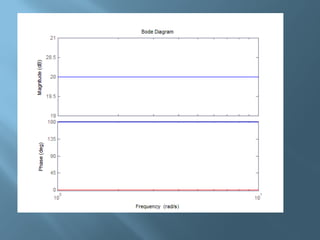
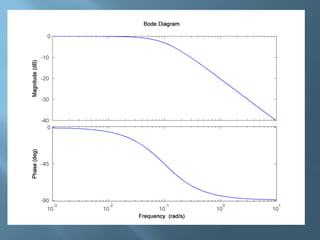
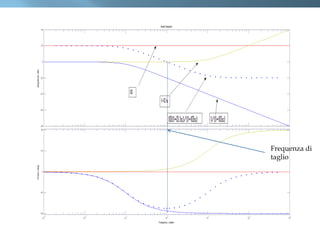
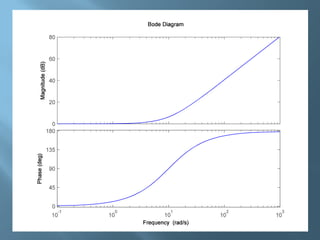
Il documento discute i diagrammi di Bode, che includono ampiezze e fasi, ed è caratterizzato da rappresentazioni asintotiche su scale semilogaritmiche. Viene spiegato come tracciare i diagrammi a partire dalla fattorizzazione della funzione di trasferimento, con dettagli su guadagni e frequenze di taglio. Infine, si evidenziano i vantaggi della rappresentazione logaritmica in termini di semplicità e scalabilità delle funzioni analizzate.

1. Teoria e applicazioni

2.  I diagrammi di Bode sono due:
 Diagrammi delle ampiezze
 Diagrammi delle fasi
 I diagrammi di Bode sono detti asintotici poiché
rappresentano le caratteristiche della f.d.t per
 Ciascuno di essi è riportato su scala
semilogaritmica nel seguente modo:
 Le pulsazioni vengono riportate sull’asse delle ascisse in
scala logaritmica base 10
 La fase e le ampiezze sono riportate sull’asse delle
ordinate di ciascun grafico e in scala lineare
0ω
ω
→
→ ∞

3. Si vuole tracciare il diagramma di Bode della seguente f.d.t.
1. Bisogna prima fattorizzare la funzione di trasferimento,
trasformarla cioè nella seguente forma:
' '2 2
' ' 1 1
1 2 ' '2 ' '2
' 1 1 2 2
2 2
1 1
1 2 2 2
1 1 2 2
2 2
(1 )(1 )...(1 )(1 )...
( )
2 2
(1 )(1 )...(1 )(1 )...
n n n n
h
n n n n
s ss s
s s
G j K
s ss s
s s s
δ δ
τ τ
ω ω ω ω
ω
δ δ
τ τ
ω ω ω ω
+ + + + + +
=
+ + + + + +
' ' 2 ' ' '2 2 ' '2
1 2 1 1 1 1 2 2
2 2 2 2
1 2 1 1 1 1 2 2
( 1/ )( 1/ )...( 2 )( 2 )...
( )
( 1/ )( 1/ )...( 2 )( 2 )...
n n n n
h
n n n n
s s s s
G j K
s s s s s
τ τ δ ω ω δ ω ω
ω
τ τ δ ω ω δ ω ω
+ + + + + +
=
+ + + + + +
dove

4. K è detta costante di guadagno
Per h=0 s=0, K’è detta guadagno statico
Per h=1 s=0, K’è detta costante di velocità
Per h=2 s=0, K’è detta costante di accelerazione
' '
' 1 2 1 2
' ' ' '
1 2 1 2
... ...
... ...
n n
n n
K K
τ τ ω ω
τ τ ω ω
=

5. 2. Si esprime la funzione di trasferimento
fattorizzata, in decibel
10
' '2 2
' ' 1 1
1 2 ' '2 ' '2
' 1 1 2 2
10 2 2
1 1
1 2 2 2
1 1 2 2
( ) 20log ( )
2 2
(1 )(1 )...(1 )(1 )...
20log
2 2
(1 )(1 )...(1 )(1 )...
dB
n n n n
h
n n n n
G j G j
s ss s
s s
K
s ss s
s s s
ω ω
δ δ
τ τ
ω ω ω ω
δ δ
τ τ
ω ω ω ω
=
+ + + + + +
=
+ + + + + +

6. 3. Ricordando le proprietà dei logaritmi:
log ( )
log( ) log( ) log( )
log( ) log( ) log( )
log( ) *log( )
log ( )
log ( )
log ( )
b
b
c
b
c
a
ab a b
a
a b
b
a b a
a
a
b
a b
= +
= −
=
=
=

7. ' ' '
10 10 1 10 2
' '2 2
1 2
10 10' '2 ' '2
1 1 2 2
10 1 10 2 10
2 2
1 2
10 10' '2 ' '2
1 1 2 2
( ) 20(log log 1 log 1
2 2
log 1 log 1
log 1 log 1 log
2 2
log 1 log 1 )
dB
n n n n
n n n n
G j K s s
s ss s
s s h s
s ss s
ω τ τ
δ δ
ω ω ω ω
τ τ
δ δ
ω ω ω ω
= + + + + +
+ + + + + + +
− + − + − • +
− + + − + +

8. 4. Ricordando la definizione di modulo di una
quantità complessa
Il modulo in decibel diventa:
2 2
x jy x y+ = +
' ' 2 ' 2
10 10 1 10 2
' '2 2
1 2
10 10' '2 ' '2
1 1 2 2
2 2
10 1 10 2 10
2 2
1 2
10 102 2
1 1 2 2
( ) 20(log log 1 ( ) log 1 ( )
2 2
log 1 log 1
log 1 ( ) log 1 ( ) log
2 2
log 1 log 1 )
dB
n n n n
n n n n
G j K
s ss s
h
s ss s
ω τ ω τ ω
δ δ
ω ω ω ω
τ ω τ ω ω
δ δ
ω ω ω ω
= + + + + +
+ + + + + + +
− + + + − • +
− + + − + +

9.  Per il diagramma delle fasi, lo sfasamento sarà
dato dalla somma di tutti gli sfasamenti
' '
1 2
'
'
1 2
( )
0
( ) ( ) ( )
1 1
( ) ( )
0 1 1
imm
arctg
re
arct arctg arctg
k
arctg n arctg arctg
ϕ
ωτ ωτ
ϕ
ωτ ωτω
→
= + + +
 
+ − + − + − 
 

10. 5. Si noti che possiamo scomporre la f.d.t
espressa in dB, nelle seguenti parti:
Ciò ci permette di scomporre il suo grafico in altri grafici più semplici
'
10
' 2
10 1
' 2
10 2
' 2
1
10 ' '2
1 1
' 2
2
10 ' '2
2 2
20 log
20 log 1 ( )
20 log 1 ( )
2
20 log 1
2
20 log 1
n n
n n
K
s s
s s
τ ω
τ ω
δ
ω ω
δ
ω ω
+ •
+ • +
+ • +
+ • + +
+ • + +
2
10 1
2
10 2
10
2
1
10 2
1 1
2
2
10 2
2 2
20 log 1 ( )
20 log 1 ( )
20 log
2
20 log 1
2
20 log 1
n n
n n
h
s s
s s
τ ω
τ ω
ω
δ
ω ω
δ
ω ω
− • +
− • +
− • •
− • + +
− • + +

11. Ricordiamo la definizione di decade
Siamo in scala logaritmica e, gli unico intervalli uguali sono quelli che vanno da
una decade all’altra, cioè di 10 in 10 . Esempio, l’intervallo 0.5-5 , 50-500.
In figura è riportato un esempio

12. 6. Si eseguono delle approssimazioni visto che
stiamo parlando di diagrammi asintotici.
Analizziamo il grafico di ogni singolo termine per
poi procedere alla sovrapposizione di tutti
0ω
ω
→
→ ∞

13. Retta parallela all’asse x con sfasamento
Modulo
Es: G(s)= 1
|G(s)|=20
( )G s K=
'
0
0arctg
K
ϕ
 
= = 
 
10( ) 20 logG s K= 

15.  G(s)=10
|G(s)|=20
φ=0°
 G(s)=-10
|G(s)|=20
φ=180°

17.  n è la molteplicità del polo o dello zero
 Siccome stiamo tracciando un diagramma asintotico, si
osserva una decade prima del polo (zero) e una decade
dopo. Il grafico sarà quello di una semiretta con pendenza –
(+) n*20dB/decade con origine sull’asse delle ascisse, una
decade prima.
 In corrispondenza dello zero o del polo si commette un
errore di 3 dB nel tracciare il grafico asintotico.
 Si definisce frequenza di taglio, quella frequenza in cui il
grafico taglia l’asse delle ascisse
2
10
2
10
20 log 1 ( )
20 log 1 ( )
1
n
n
n arctg
τω
τω
τω
ϕ
+ • +
− • +
 
=± •  
 

18.  G(s)=1+0.1s
 Es
 ω <= 1, (una decade prima dello zero)
|G(s)|=0 φ=0
 ω =10,
|G(s)|=20*log1021/2 φ=45°
 ω >= 100, (una decade dopo lo zero)
|G(s)|=20 dB φ=90°
2
10( ) 20 log 1 (0.1 )
0.1
1
G s
arctg
ω
ω
ϕ
= +
 
=  
 


20.  Es G(s)=1/(1+10s)
 ω <= 0.01, (una decade prima del polo)
|G(s)|=0 φ=0
 ω =0.1,
|G(s)|=-20*log1021/2 φ=−45°
 ω >= 1, (una decade dopo il polo )
|G(s)|=-20 dB φ=−90°
2
10( ) 20 log 1 (10 )
10
1
G s
arctg
ω
ω
ϕ
=− +
 
= −  
 


22.  Sia data una f.d.t data dal prodotto delle
precedenti
 I diagrammi di Bode sono dati dalla
sovrapposizione degli altri tre
10(1 0.1 )
( )
(1 10 )
s
G s
s
+
=
+

23. Frequenza di
taglio

24.  Es G(s)=(1+0.1s)2
2
10( ) 2 20 log 1 (0.1 )
0.1
2
1
G s
arctg
ω
ω
ϕ
= +
 
=  
 
 

ω <= 1, (una decade prima dello zero)
|G(s)|=0 φ=0
ω =10
|G(s)|=40*log1021/2 φ=90°
ω >= 100, (una decade dopo lo zero)
|G(s)|=40 dB φ=180°

26.  Es G(s)=1/(1+10s)2
 ω <=0.0 1, (una decade prima del polo)
|G(s)|=0 φ=0
 ω =0.0 1,
|G(s)|=-40*log1021/2 φ=90°
 ω >= 1, (una decade dopo il polo)
|G(s)|=-2*20 dB φ=−180°
2
10( ) 2 20 log 1 (10 )
10
2
1
G s
arctg
ω
ω
ϕ
=− +
 
= −  
 
 


28.  G(s)=sn
 |G(s)|=n*log10 s
 φ=n*arctg(jω/0)=n 90°
Es:
G(s)=s
 |G(s)|=log10 s
 φ=arctg(jω/0)=90°

30.  G(s)=s-n
 |G(s)|=-n*log10 s
 φ=-n*arctg(jω/0)=−n 90°
Es:
G(s)=1/s
 |G(s)|=-log10 s
 φ=-arctg(jω/0)=−90°

32. 2
2
1
( )
1 2
n n
G s
s
s
ξ
ω ω
=
+ +
( )
2
2
1,2
2
2
1,2
4
1
4
n n n
n
n
ξ ξ
ω ω ω
ω
ω
ω ω ξ ξ
 
− ± − 

=
= − ± −

34.  I vantaggi di una rappresentazione in scala
logaritmica sono i seguenti:
 Alcune funzioni semplici come monomi, binomi,
…polinomi assumono una forma particolarmente
semplice
 Possibilità di rappresentare ampie scale di variazione
 Una funzione più complessa può essere espressa
come somma di più funzioni semplici e quindi, ogni
grafico di funzioni più complesse, può essere dato
dalla sovrapposizione di grafici di semplici funzioni