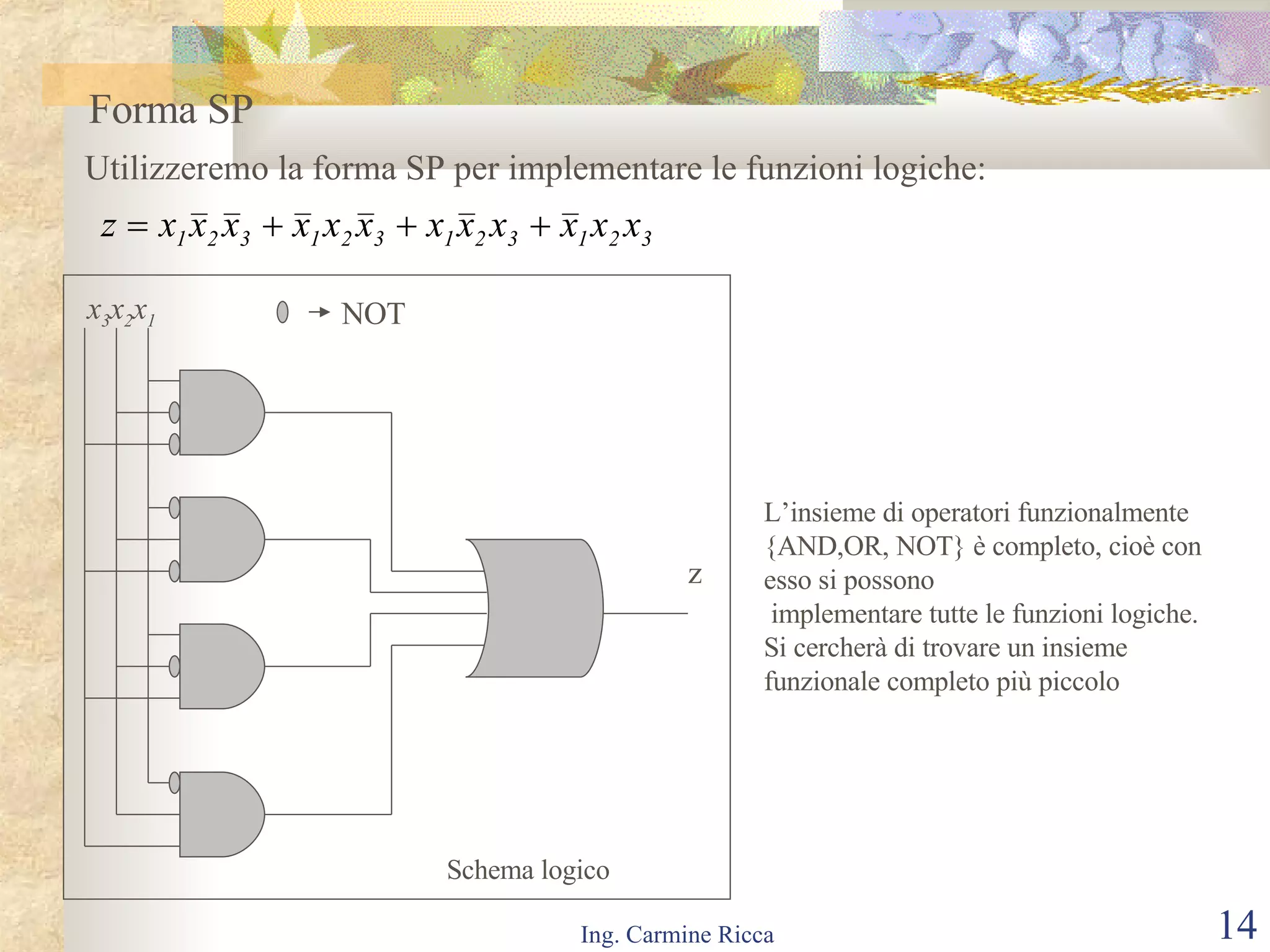
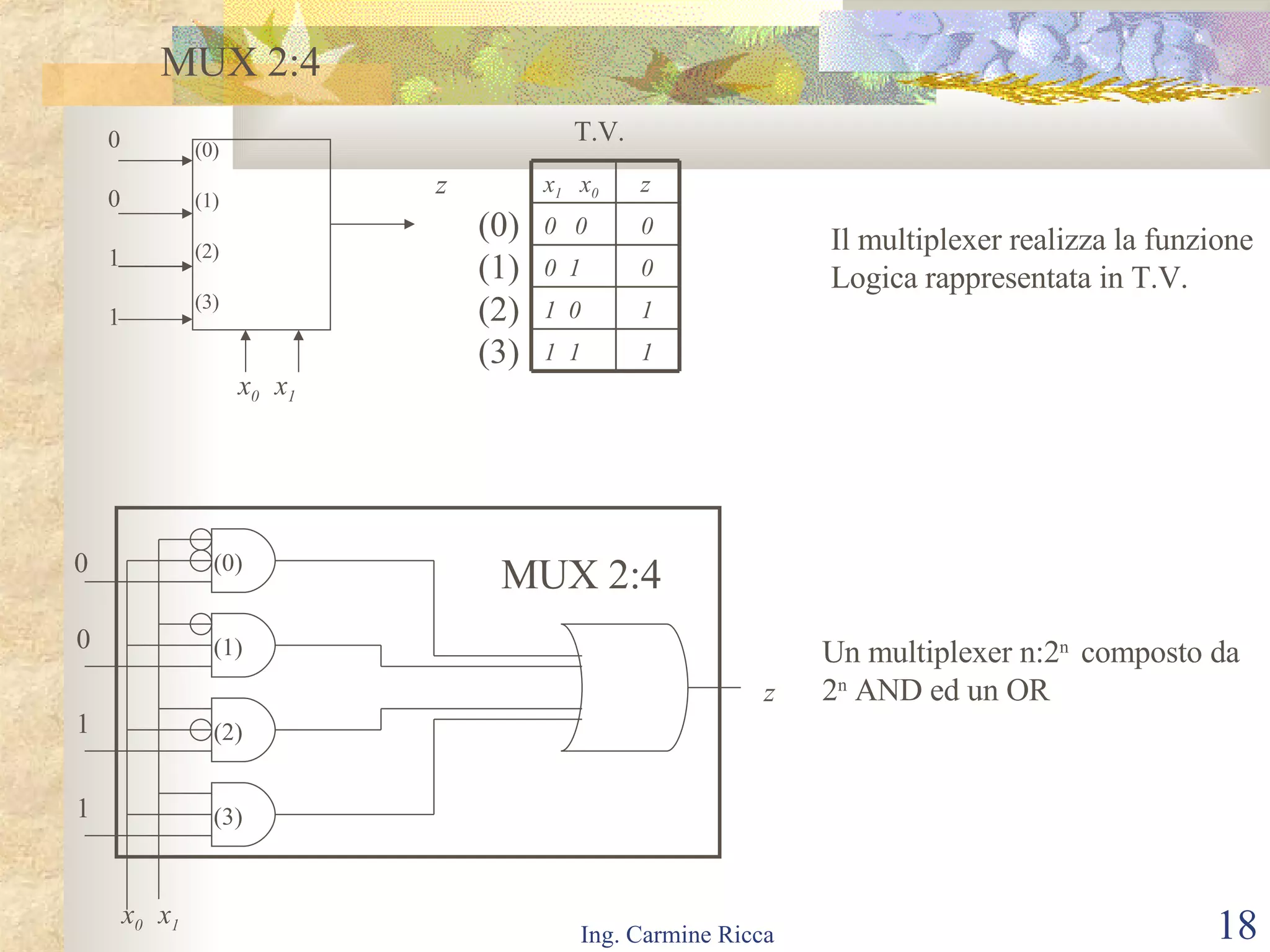
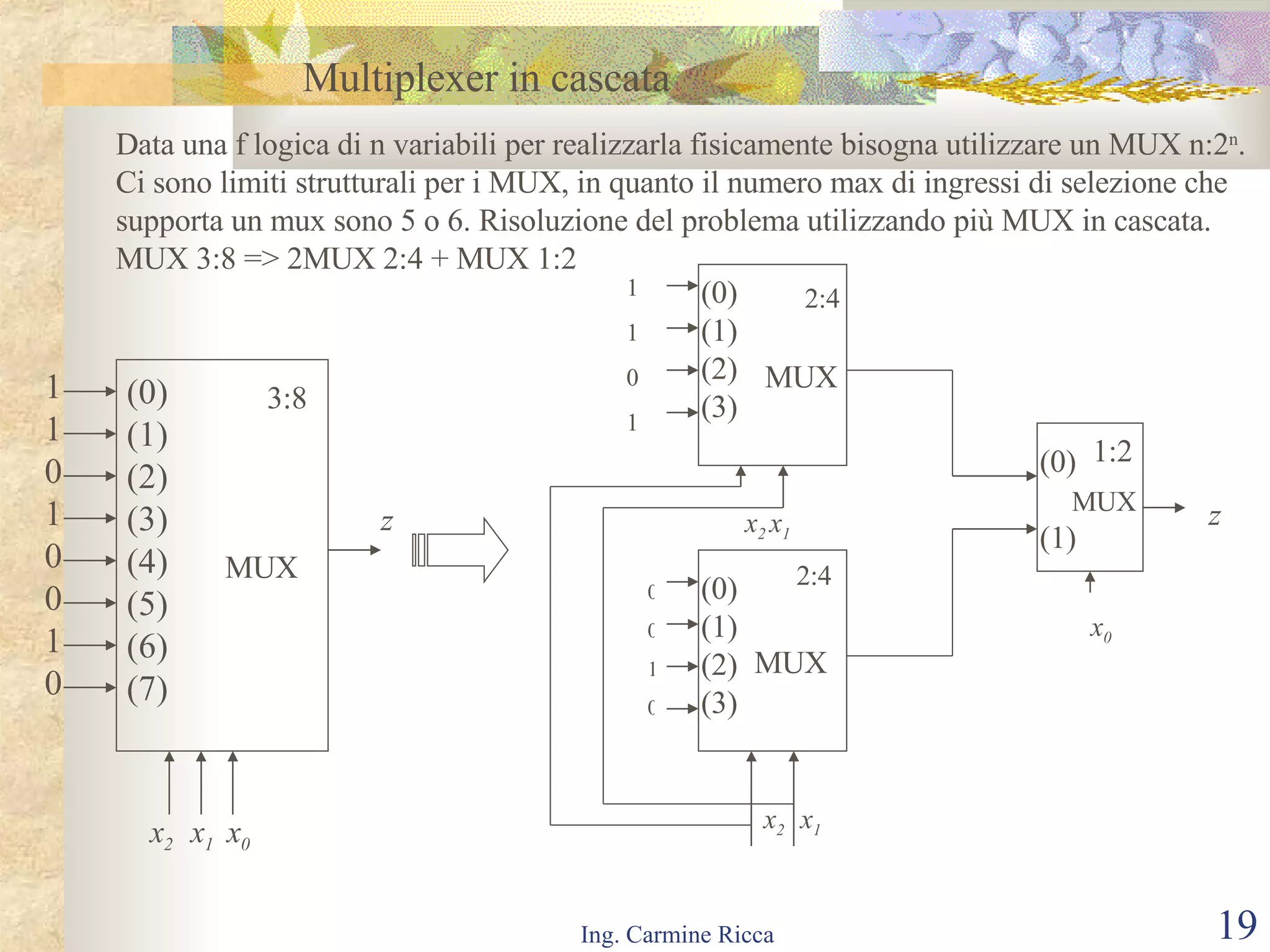
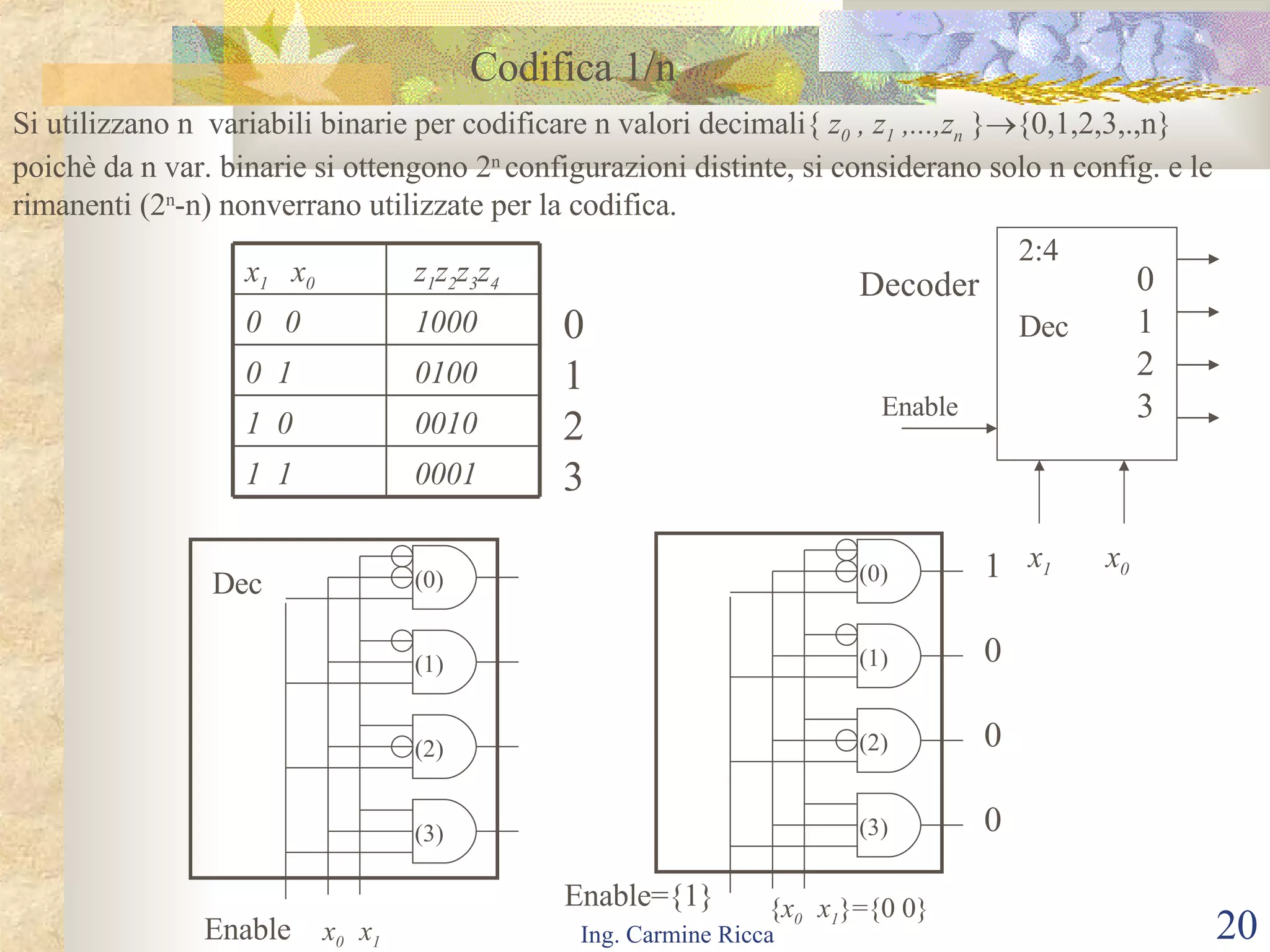
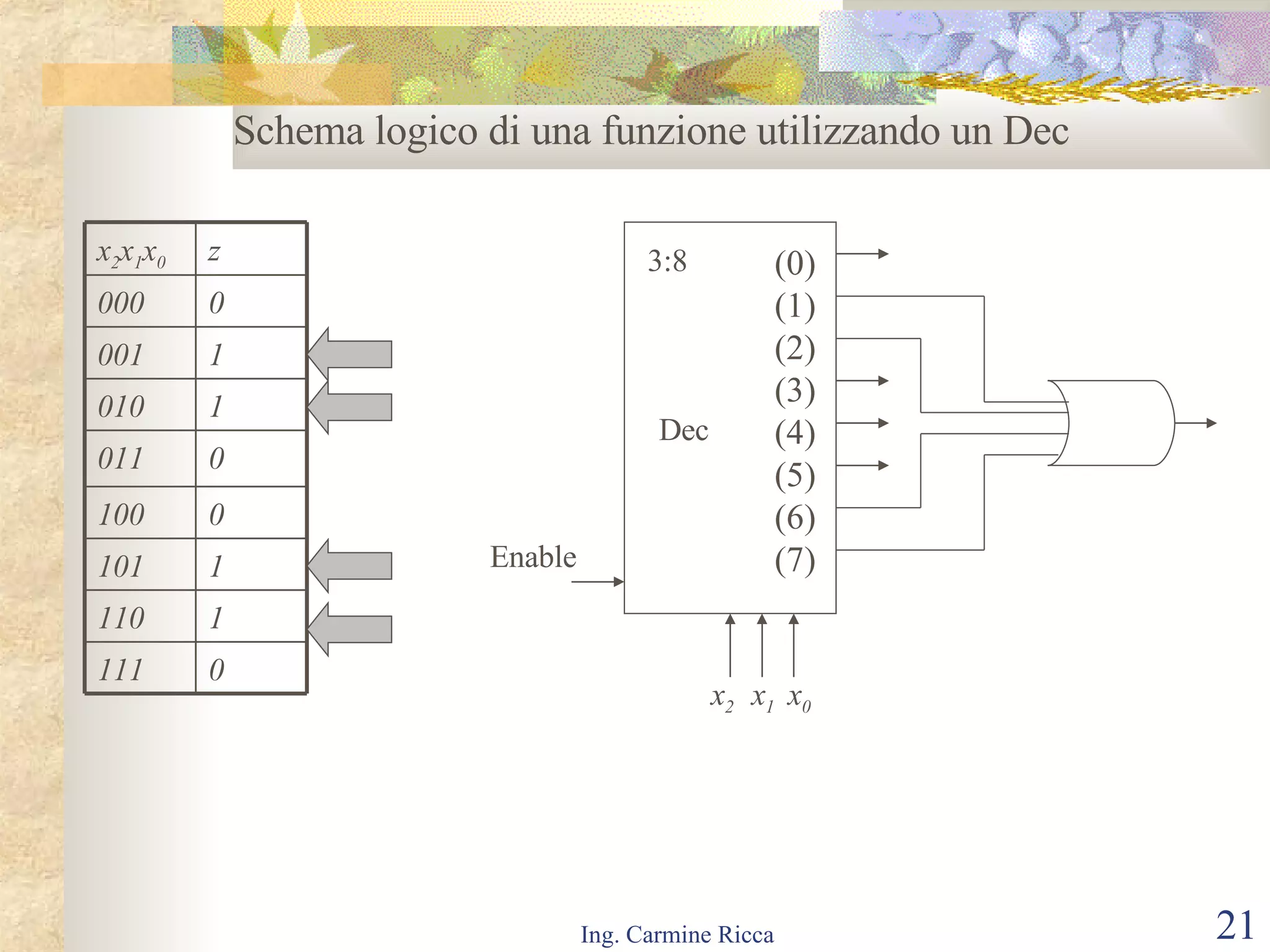
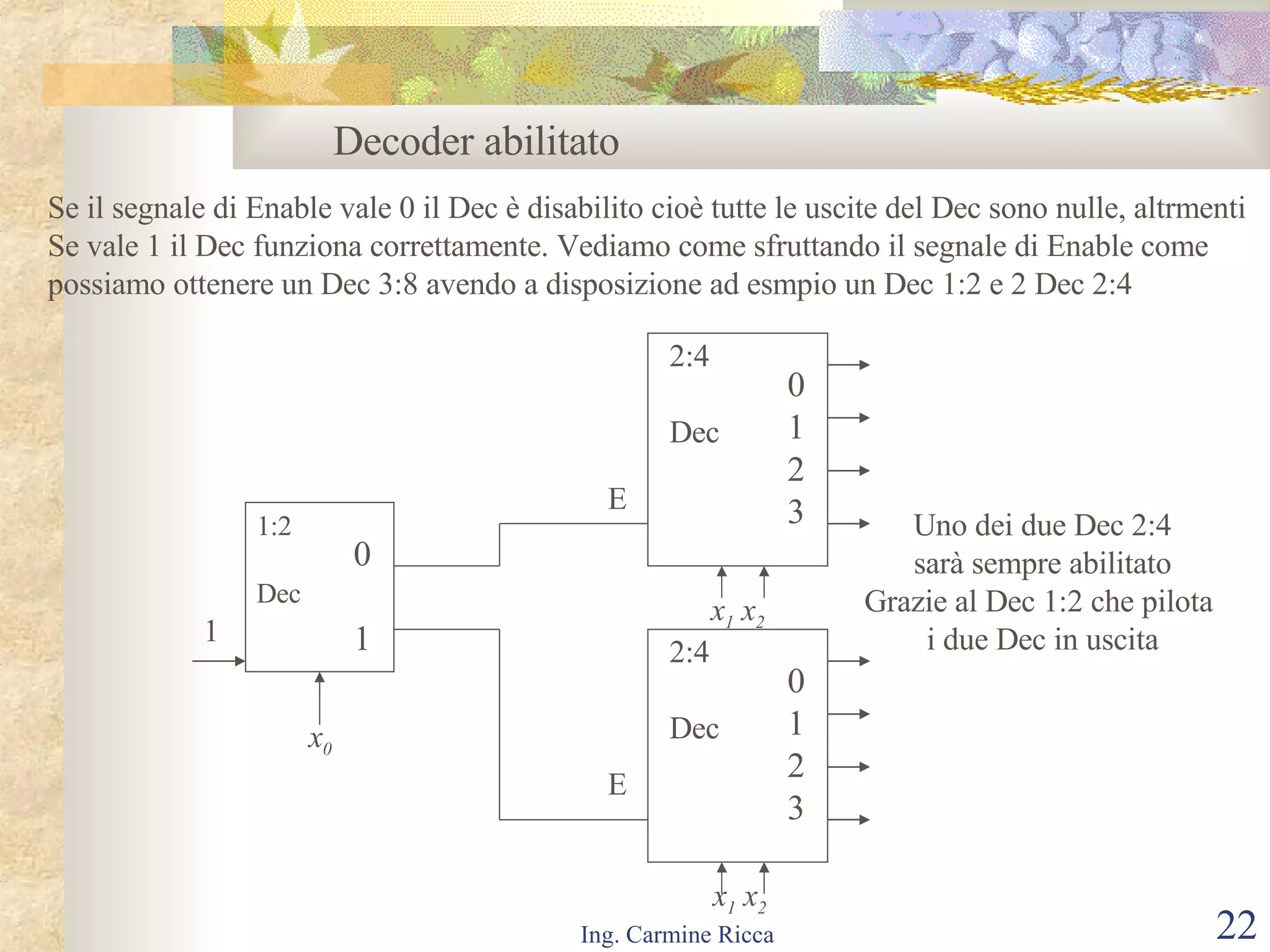
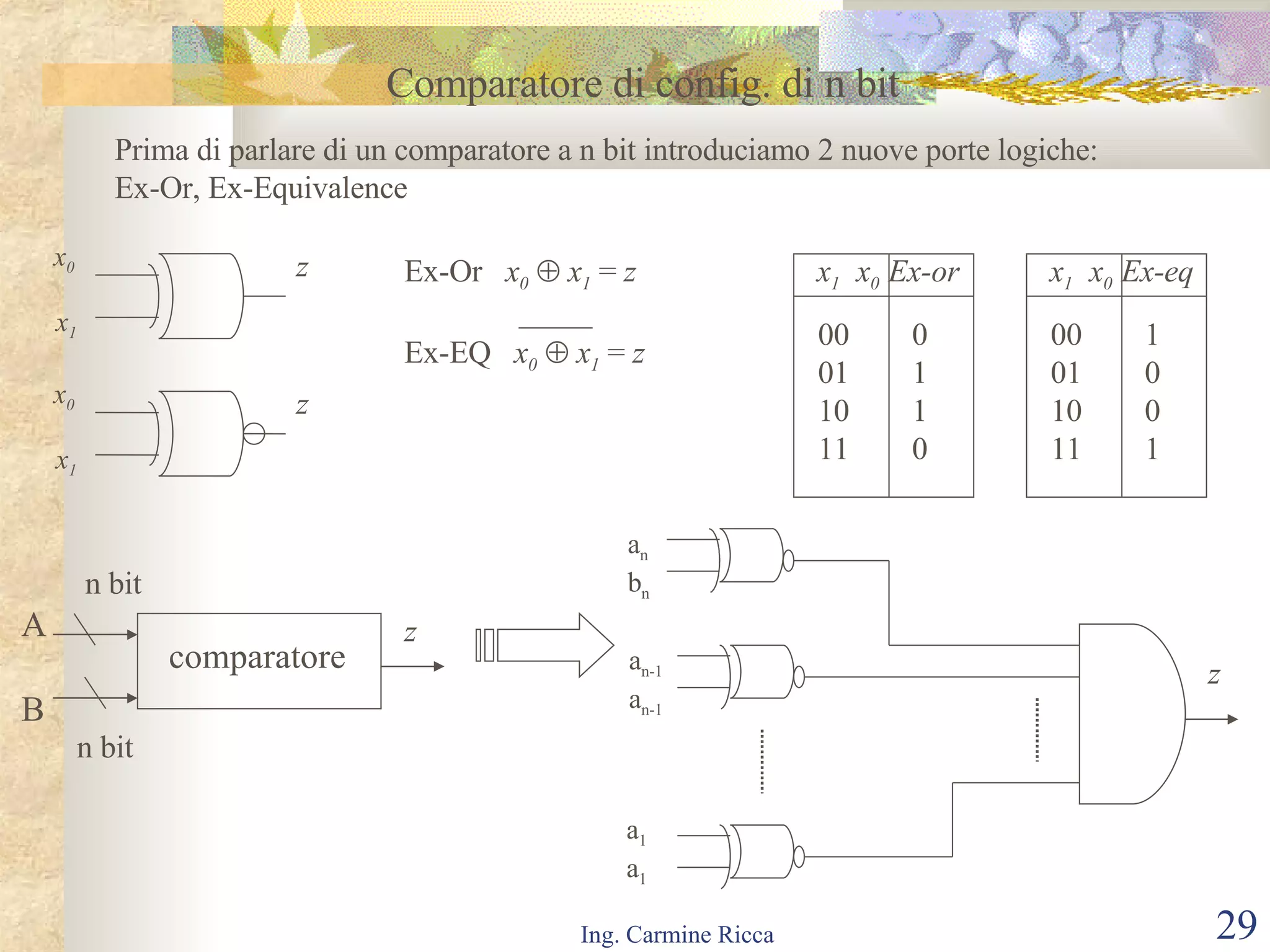
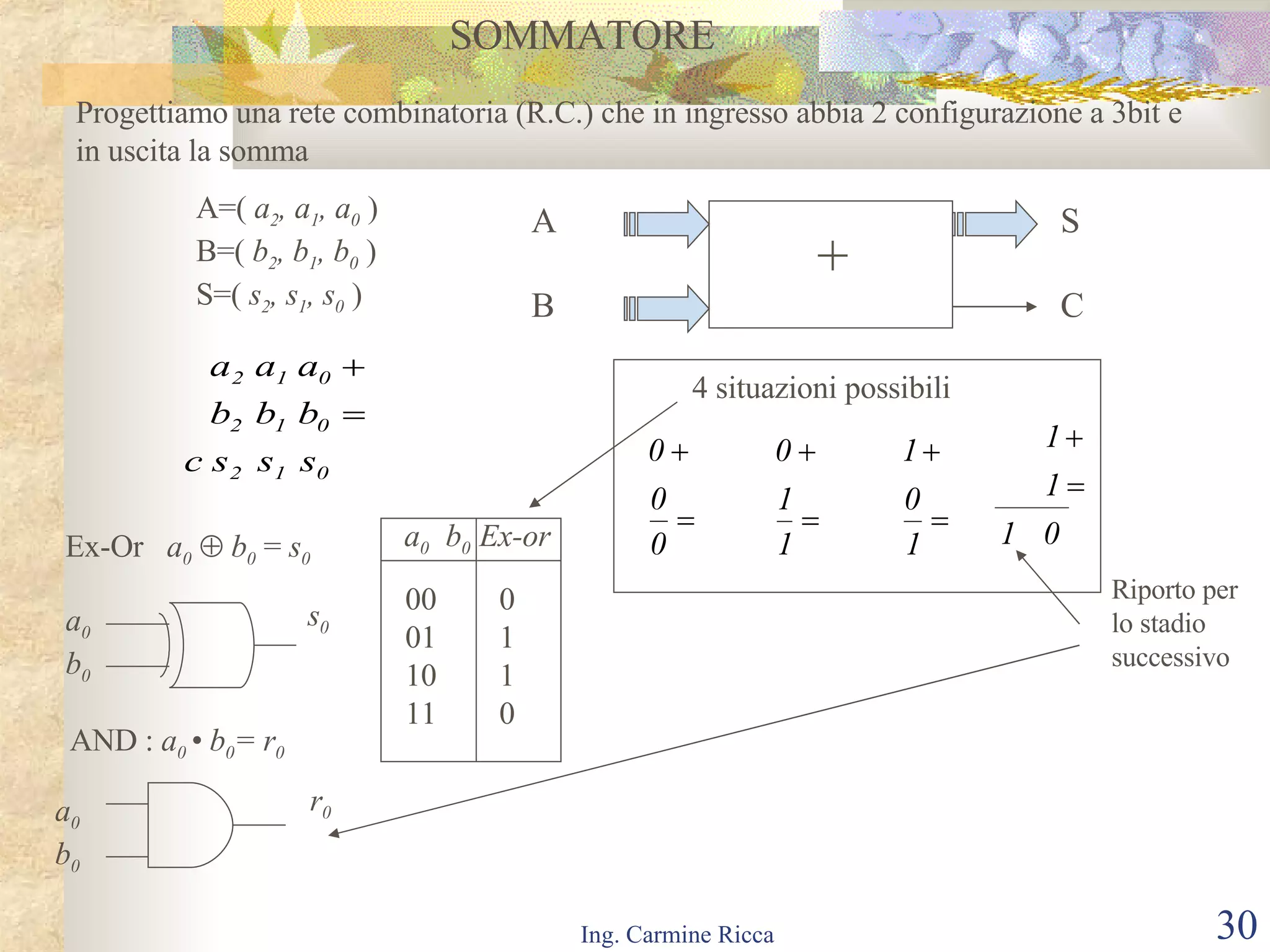
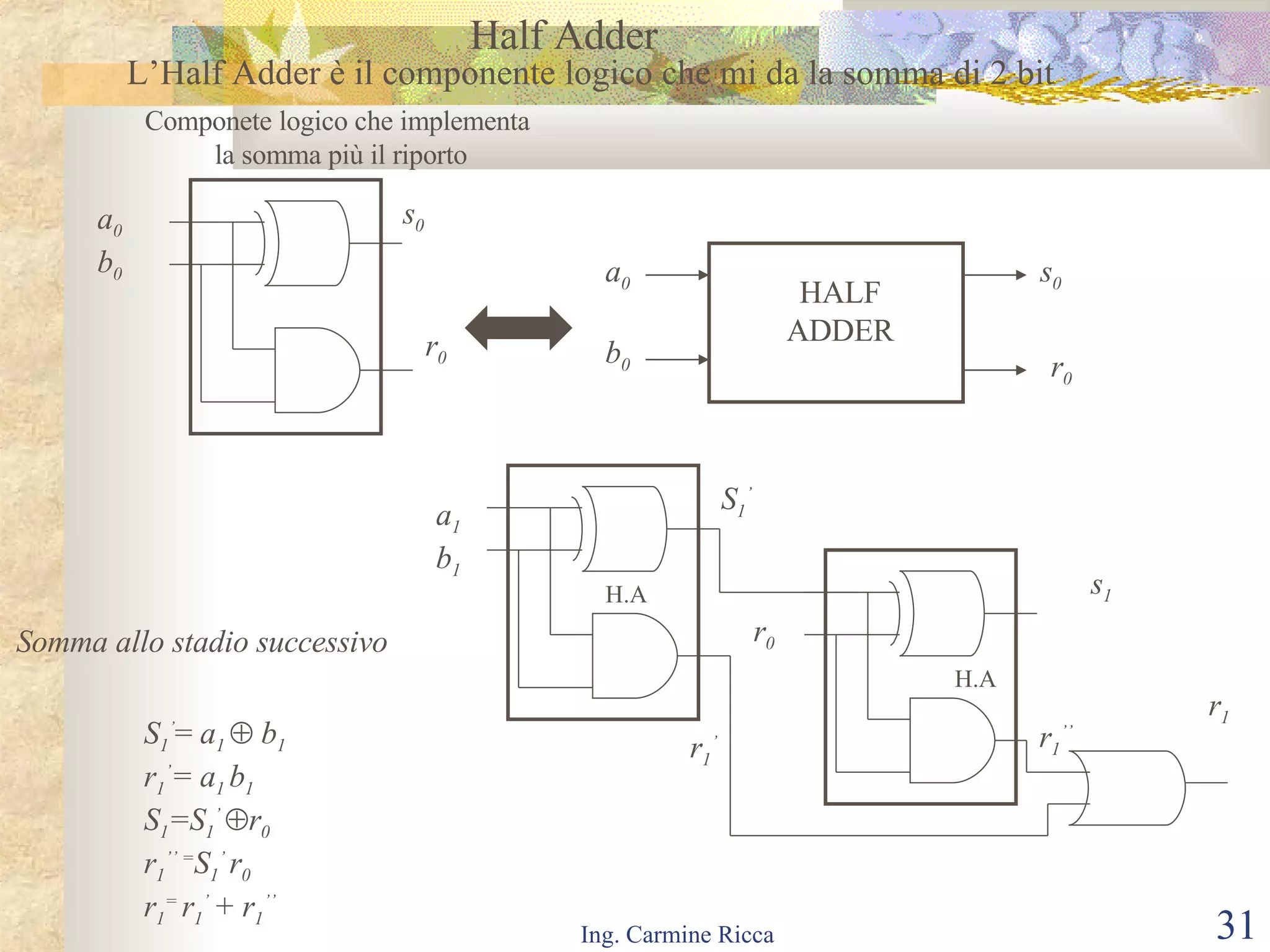
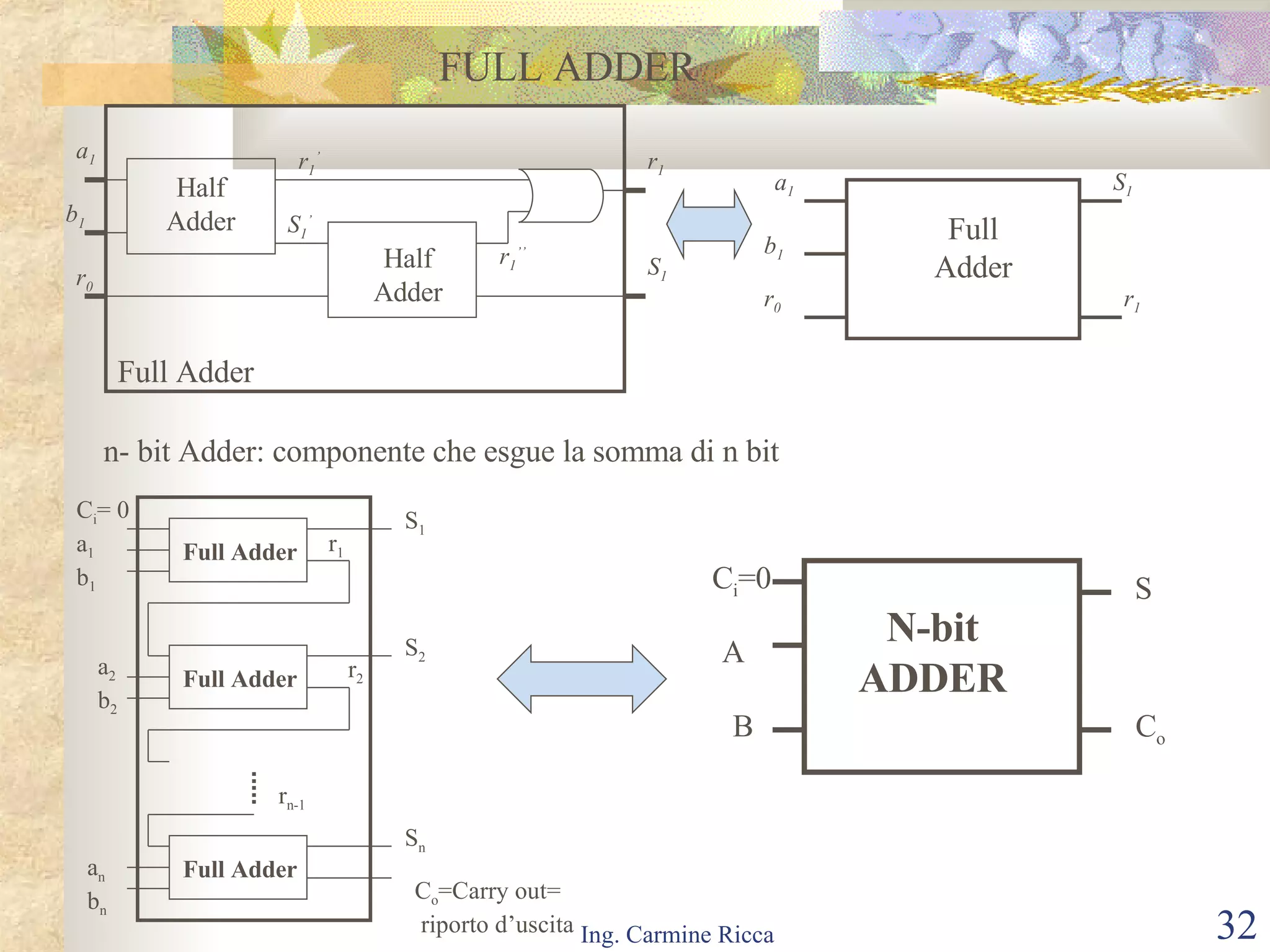
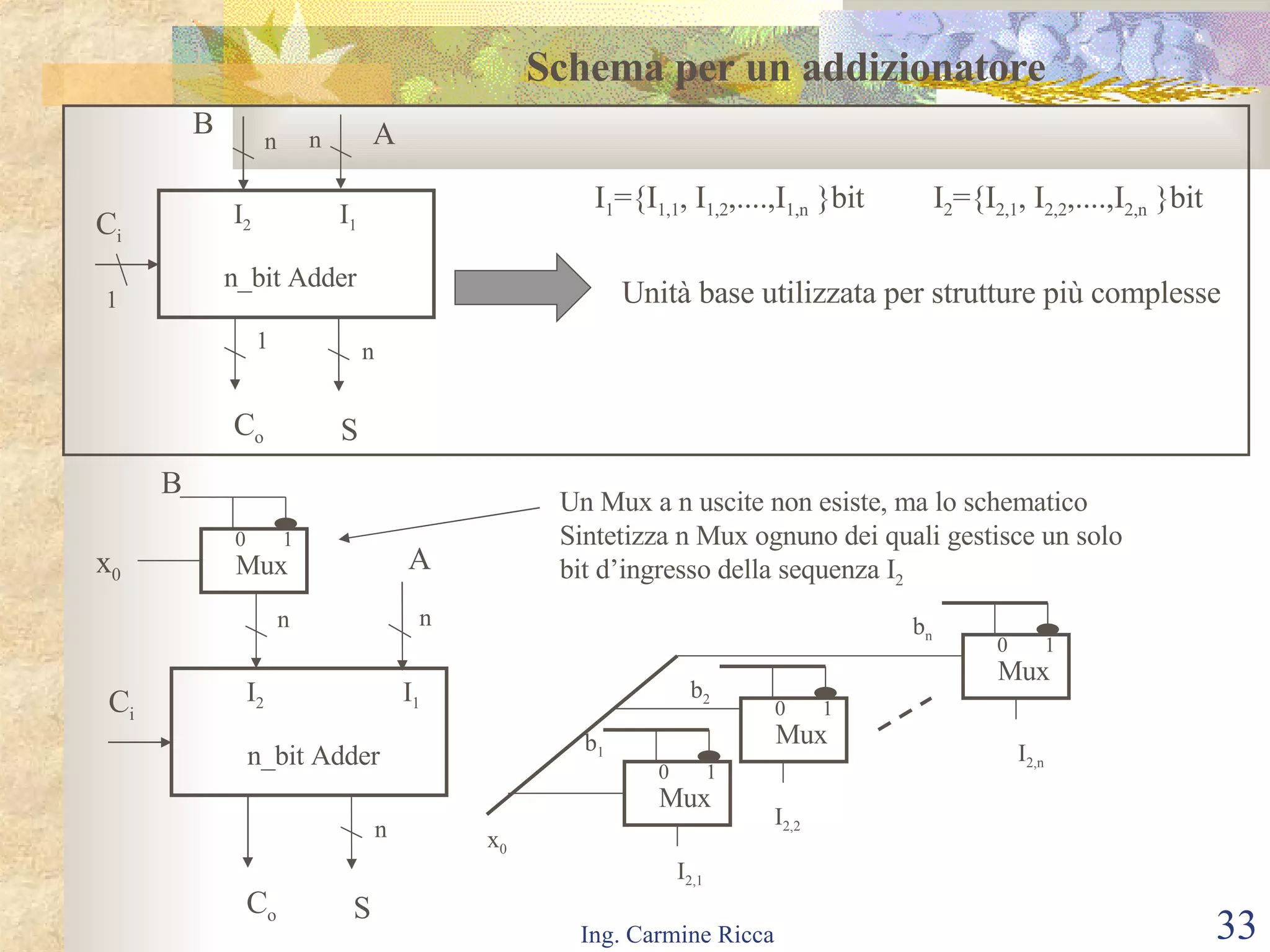
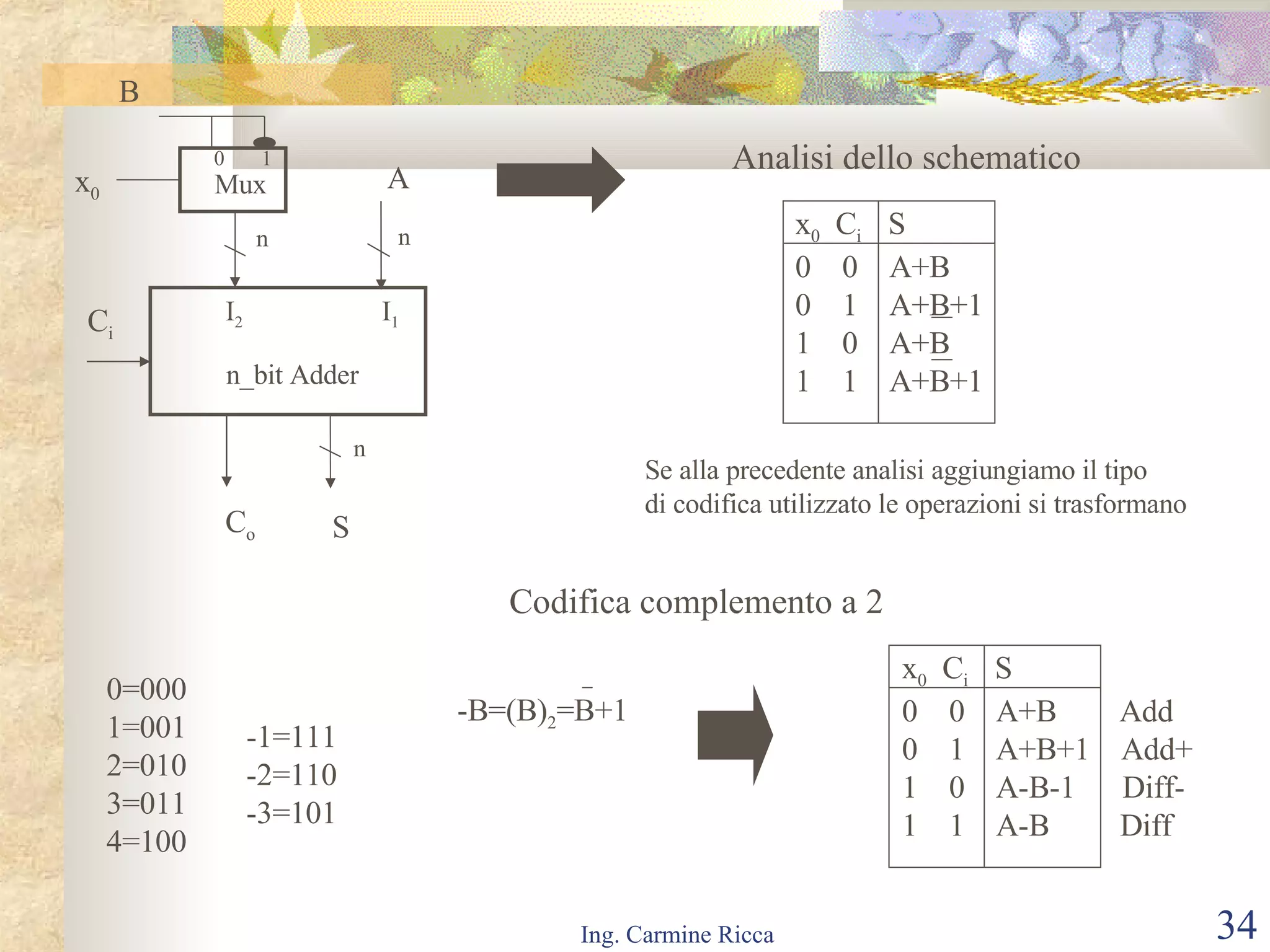
Il documento descrive i segnali digitali e il loro trattamento attraverso campionamento e quantizzazione, evidenziando concetti come il segnale campionato e l'errore di quantizzazione. Viene inoltre introdotto il concetto di reti logiche combinatorie, spiegando la loro struttura e funzionamento, così come l'importanza di tecniche come le mappe di Karnaugh per semplificare le espressioni logiche. Infine, si tratta l'uso di multiplexer e decoder per realizzare reti logiche, includendo aspetti pratici e tecnici della progettazione.
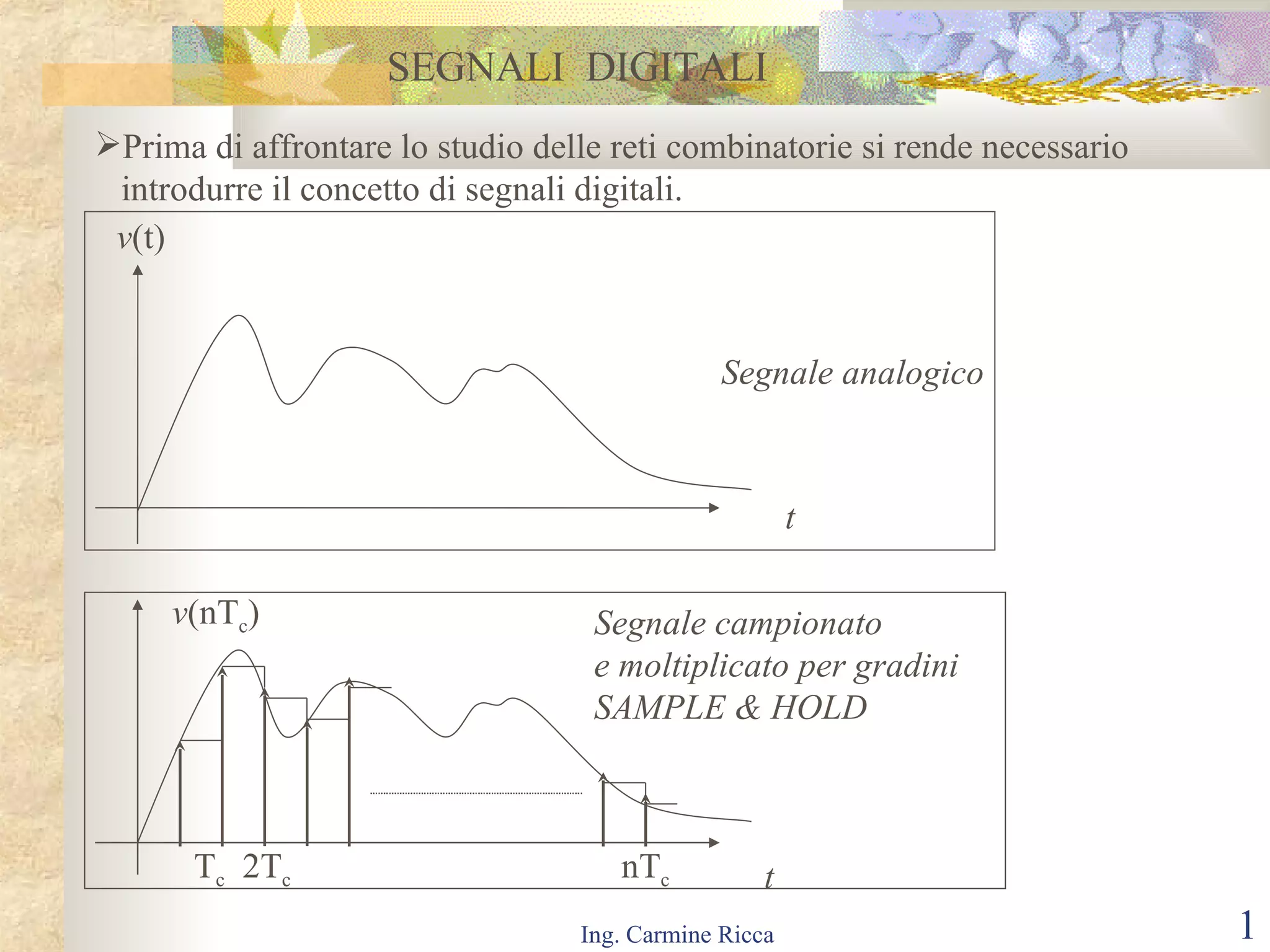
![Il segnale campionato v(nT c ) si ottiene moltiplicando v(t) per un treno d’impulsi quello che si ottiene è una sequenza di valori campionati negli istanti nT c con n = 0, 1, 2 ......., N, tali valori continui rappressentano l’altezza dei gradini di base T c . L’informazione associata al segnale compreso in un generico intervallo [( n-1 ) T c , nT c ] viene completamente persa, rimane traccia dell’informazione originaria nella gradinata ottenuta con la procedura sample & hold. Segnale campionato t v (nT c ) T c 2T c nT c SAMPLE & HOLD](https://image.slidesharecdn.com/reti-logic-1193060233489186-2/75/Reti-Logic-2-2048.jpg)
![QUANTIZZAZIONE La dinamica dei campioni v(nT c ) può assumere un’infinità di valori, per ridurre la complessità del sistema si può procedere alla discretizzazione dell’asse delle ordinate imponendo un ulteriore vincolo sui campioni: la dinamica di v(t) può assumere soltanto un numero finito di valori. t v (nT c ) T c 2T c nT c v (nT c )= v [n]+ e q [n] v (nT c ) segnale campionato v [n] segnale quantizzato e q [n] errore di quantizzazione v [n] T c = periodo di campionamento F c = 1/T c frequenza di campionamento](https://image.slidesharecdn.com/reti-logic-1193060233489186-2/75/Reti-Logic-3-2048.jpg)
![Caratterizzazione Statistica dell’Errore di Quantizzazione e q 2 2 N-1 - -2 -2 N-1 0 Un qualsiasi campione del segnale che cade nell’intervallo [0, ] verrà settato al valore di per cui l’esursione dell’errore di quant. va da 0 a . passo di quantizzazione 2 N livelli di quant. 1/ P(e q ) e q P(e q )= densità di probabilita di e q uniformemente distribuito tra 0 e V.M. = valor medio = /2 Potenza del rumore = 2 /12](https://image.slidesharecdn.com/reti-logic-1193060233489186-2/75/Reti-Logic-4-2048.jpg)
![Schema a blocchi di un sistema di conversione Analogico-Digitale F T Filtro antialiasing Sample & Hold Quantizz. Passo Codificatore b bit u (t) û (t) û (nT c ) û [n] Sequenza di b bit ADC ADC = Analogic Digital Converter N.B. Il filtro antialising serve per una corretta riconversione da digitale ad analogico](https://image.slidesharecdn.com/reti-logic-1193060233489186-2/75/Reti-Logic-5-2048.jpg)