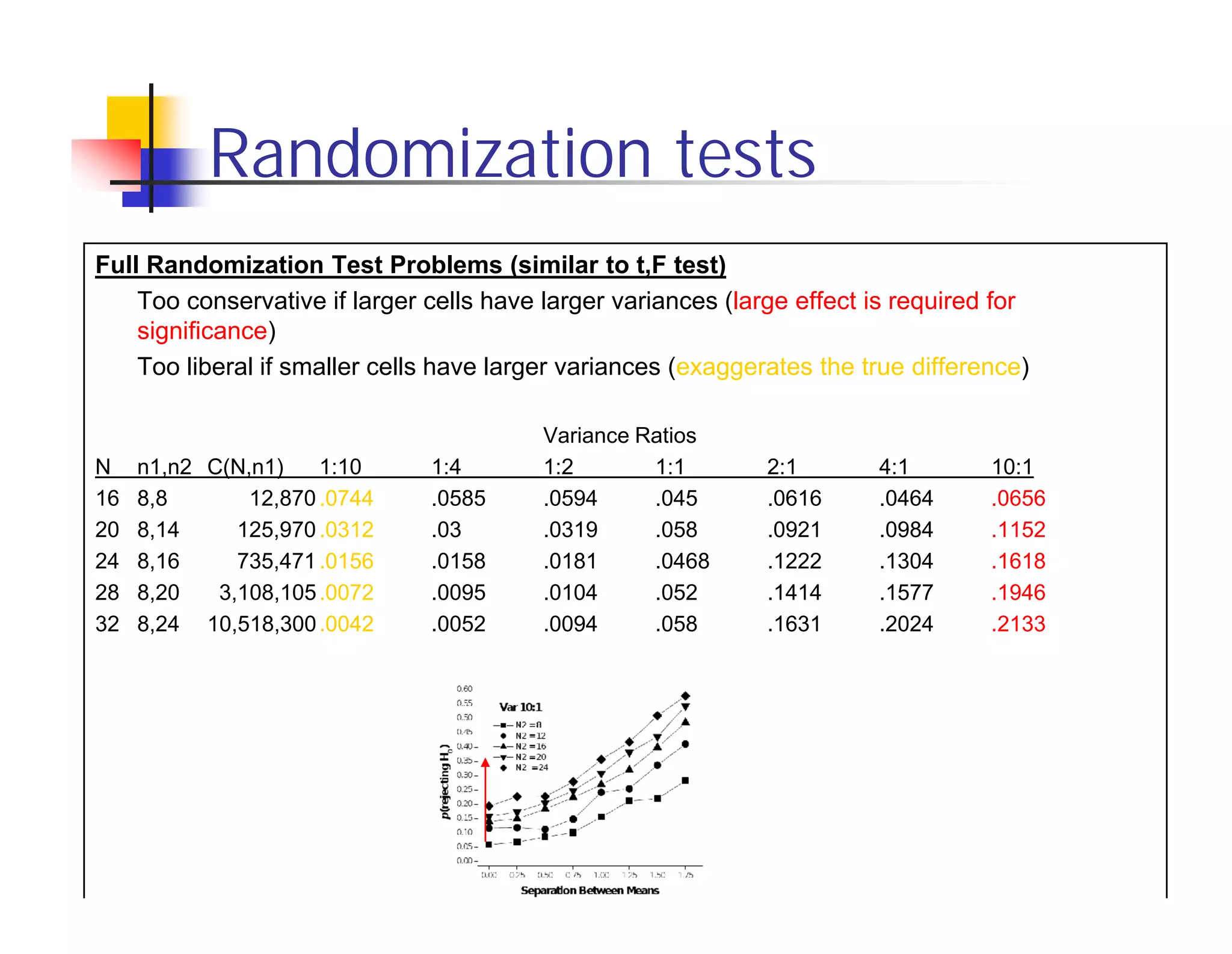
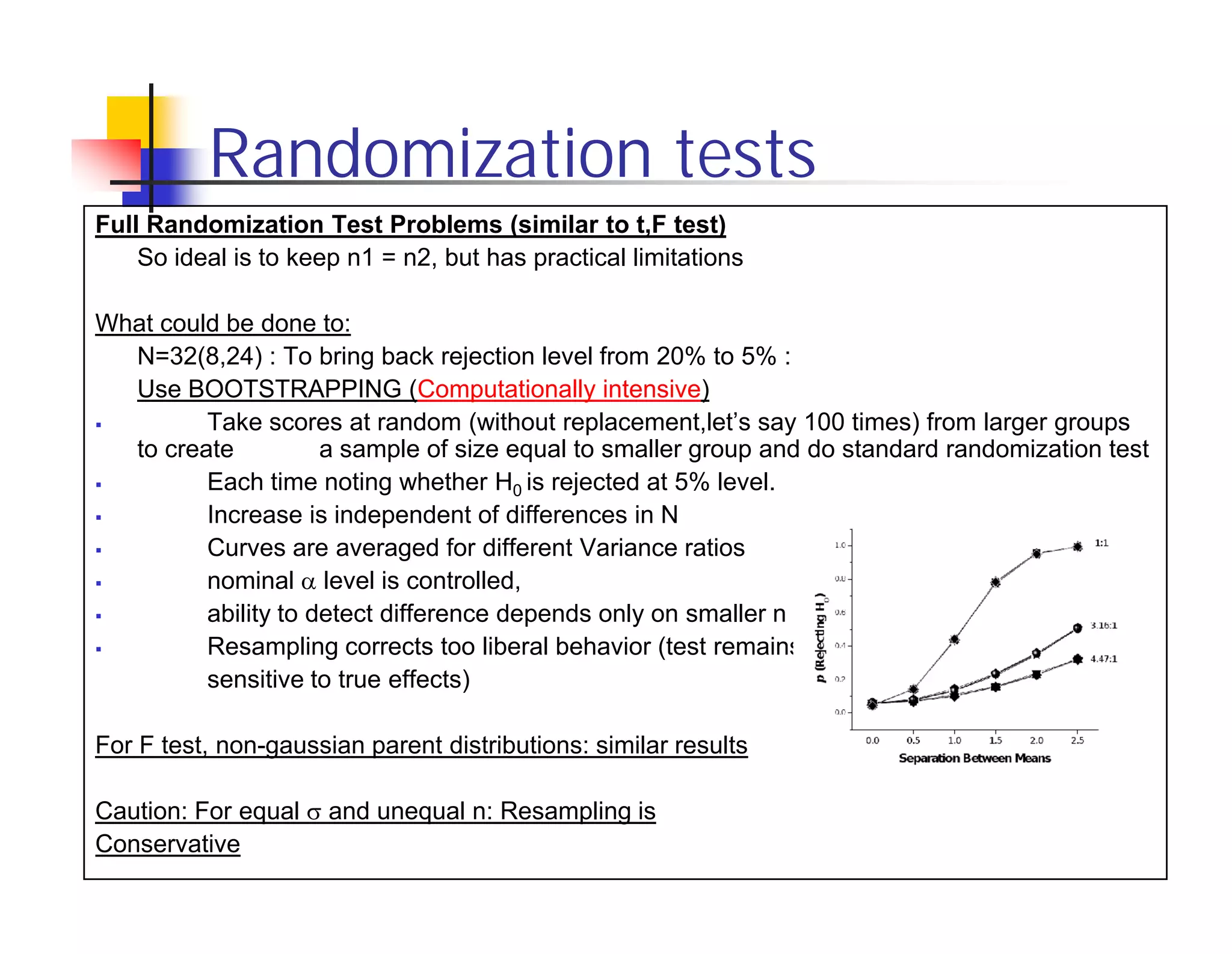
Randomization tests provide an alternative to t-tests and F-tests that does not rely on assumptions of normality or random sampling. However, randomization tests can be too liberal or conservative depending on differences in sample sizes. Bootstrapping and Gill's algorithm can help address these issues. Bootstrapping resamples the larger sample to match the size of the smaller sample, controlling for liberal bias. Gill's algorithm uses Fourier expansion to efficiently calculate p-values from all permutations, reducing computational cost compared to full enumeration. However, conservative bias remains a challenge without a known solution.

1. Randomization Tests – unequal-N,
unequal-σ problem
AK Dhamija

2. Agenda
Assumptions of t, F tests
Randomization tests
Problems of Randomization Test
Too liberal
Too conservative
Computationally Intensive
Solving the problems
Resampling
Gill’s algorithm

3. Assumptions of t, F tests
The two samples are each drawn from
normal distributions.
The two samples are drawn randomly from
their respective populations.
RANDOMIZATION TESTS TACKLE THESE
UNREALISTIC ASSUMPTIONS

4. Randomization tests
An Example Comparing t-Test and Randomization Test Results
Two fertilizers (A and B) that are randomly applied to a type of sunflower seed.
The maximum heights reached (in feet) are recorded after some time period.
All Other Factors are constant
Null hypothesis : no difference between fertilizers A and B with respect to sunflower height.
Alternative hypothesis : fertilizer A is superior to fertilizer B on average with respect to sunflower height.
Sample Fertilizer Height (ft)
1 A 9.9
2 B 9.6
3 B 9.7
4 B 9.4
5 A 10.1
6 B 9.5
7 A 9.9
8 B 9.6 Total 462 (11 !/ 5! 6!) permutations
9 A 9.5 5 of the 462 showed mean difference of 9.920 – 9.533 = 0.387
10 A 10.2 p-value = 5/ 462 = 0.0108 => Reject H0 (t-test also rejects)
11 B 9.4 = > fertilizer A outperforms fertilizer B
So t-test provides reasonably good approximation to randomization test

5. Randomization tests
Randomization Tests do not consider normality, random sampling, equal variances, or
other assumptions.
The conclusion was based solely on the observed results, and the fact that the fertilizers
were randomly assigned.
Why randomization tests then are not widely used, nor addressed in many statistical
texts.
The number of computations with larger sample sizes becomes astronomical
With two samples, each of size 30, there are over 1.18 * 1017 possible permutations!
But randomization tests becomes sensitive to heteroscedasticity when the cells are
unequal in size
Approximate randomization Tests (selecting few combinations)
Unstable – (statistics may vary)
Unreplicable

6. Randomization tests
Full Randomization Test Problems (similar to t,F test)
Too conservative if larger cells have larger variances (large effect is required for
significance)
Too liberal if smaller cells have larger variances (exaggerates the true difference)
Variance Ratios
N n1,n2 C(N,n1) 1:10 1:4 1:2 1:1 2:1 4:1 10:1
16 8,8 12,870 .0744 .0585 .0594 .045 .0616 .0464 .0656
20 8,14 125,970 .0312 .03 .0319 .058 .0921 .0984 .1152
24 8,16 735,471 .0156 .0158 .0181 .0468 .1222 .1304 .1618
28 8,20 3,108,105 .0072 .0095 .0104 .052 .1414 .1577 .1946
32 8,24 10,518,300 .0042 .0052 .0094 .058 .1631 .2024 .2133

7. Randomization tests
Full Randomization Test Problems (similar to t,F test)
So ideal is to keep n1 = n2, but has practical limitations
What could be done to:
N=32(8,24) : To bring back rejection level from 20% to 5% :
Use BOOTSTRAPPING (Computationally intensive)
Take scores at random (without replacement,let’s say 100 times) from larger groups
to create a sample of size equal to smaller group and do standard randomization test
Each time noting whether H0 is rejected at 5% level.
Increase is independent of differences in N
Curves are averaged for different Variance ratios
nominal level is controlled,
ability to detect difference depends only on smaller n
Resampling corrects too liberal behavior (test remains
sensitive to true effects)
For F test, non-gaussian parent distributions: similar results
Caution: For equal and unequal n: Resampling is
Conservative

8. Randomization tests
Full Randomization Test Problems : Bringing Computational cost under control
Computations : (n1=10,n2=16, equal ) = C(26,10) = 26!/16!10! = 5,311,735 combinations
(larger in smaller cell) => resampling => 100 randomization tests each involves
C(20,10) = 184,756 combinations => Total 18,475,600 combinations
Gill’s Algorithm : Gill(2007) used Fourier expansion to count extreme cases.
Under H0, all combinations of data in a randomization case are equally likely
Compute proportion of cases that is as or more extreme than observed data
one tail prob = P(T>t) + p(T=2) /2
where tr is the value on rth combination
where k = 2k’ –1, K’=1 to , and F(a) is imaginary part of a
Computational Cost brought down to practical level of a PC (little more costly than F,t but faster than full
enumerations of all combinations

9. Conclusion
Assumptions of t, F tests create problems
Randomization test obviates that, but it has its own
problems
Too conservative, Too liberal, and computationally
intensive
Liberal Bias can be removed by Bootstrapping, but it
further makes it more computationally intensive
Gill’s algorithm saves computational cost
However algorithm is still asymmetric : No algorithm is
known yet to remove Conservative bias

10. References
Fisher, Ronald A. “The Design of Experiments”. 8th ed. New
York: Hafner Publishing Company Inc., 1966.
Mewhort, D.J.K, Mathew Kelly and Johns Brendan
T.“Randomization tests and the unequal-N/unequal-variance
problem”
Gill, P. M.W. (2007). Efficient calculation of p-values in linear-
statistic permutation significance tests.Journal of Statistical
computation & Simulation, 77, 55-61.