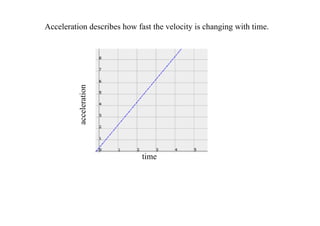
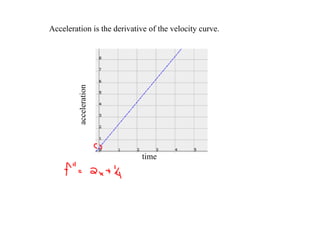
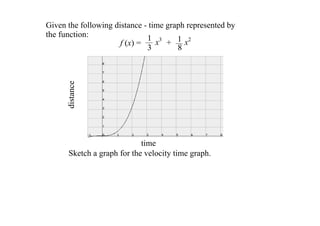
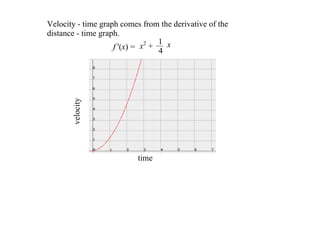
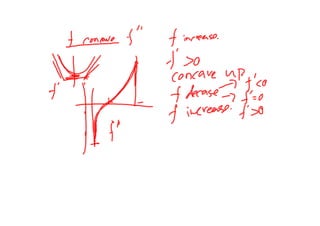
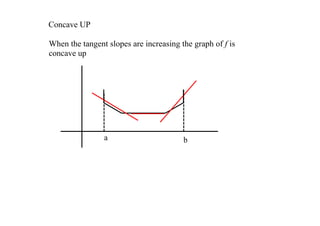
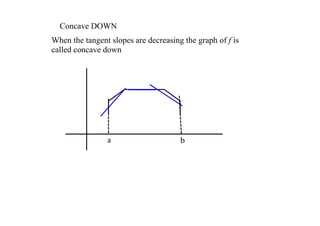
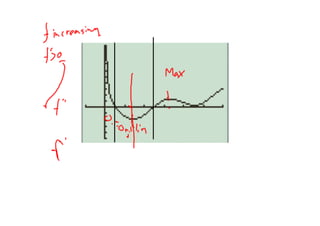
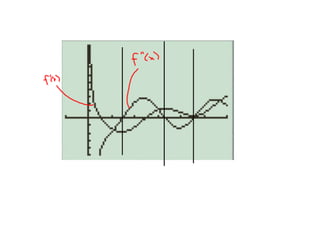
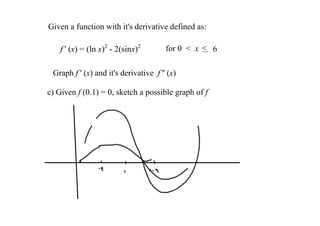
1. The document discusses distance-time and velocity-time graphs and their relationships. It defines acceleration as the derivative of velocity over time. 2. It provides an example distance-time function and asks to sketch the corresponding velocity-time graph. It also discusses how to determine if a function is increasing or decreasing based on the signs of its derivative. 3. The document ends by giving a velocity function and asking to graph its derivative and determine where the original function is increasing, where it is concave up, and to sketch a possible graph based on an initial value.

2. Given the following distance ­ time graph represented by
the function: 1 3
f (x) = x + 1 x
2
3 8
distance
time
Sketch a graph for the velocity time graph.

3. Velocity ­ time graph comes from the derivative of the
distance ­ time graph.
2 1
f '(x) = x + 4 x
velocity
time

4. Acceleration describes how fast the velocity is changing with time.
acceleration
time

5. Since f '(x) is a function we can calculate it's derivative:
f '(a + h) ­ f '(a)
f ''(a) = lim
h 0
= (f ') ' (a)
h
f ''(a) is called the second derivative of f at a
also written as:
d (dy) d2y
=
dx dx dx2

6. Acceleration is the derivative of the velocity curve.
acceleration
time

7. Remember that the derivative of a function tells you
whether the function is increasing or decreasing.
Since f '' is the derivative of f '
1. If f ''(x) > 0 on an interval, then f ' is increasing
2. If f ''(x) < 0 on an interval, then f ' is decreasing

9. Concave UP
When the tangent slopes are increasing the graph of f is
concave up
a b

10. Concave DOWN
When the tangent slopes are decreasing the graph of f is
called concave down
a b

11. Given a function with it's derivative defined as:
f ' (x) = (ln x)2 ­ 2(sinx)2 for 0 < x < 6
Graph f ' (x) and it's derivative f '' (x)
a) On which intervals is f increasing?
b) On which intervals is f concave up?
c) Given f (0.1) = 0, sketch a possible graph of f

14. Given a function with it's derivative defined as:
f ' (x) = (ln x)2 ­ 2(sinx)2 for 0 < x < 6
Graph f ' (x) and it's derivative f '' (x)
a) On which intervals is f increasing?

15. Given a function with it's derivative defined as:
f ' (x) = (ln x)2 ­ 2(sinx)2 for 0 < x < 6
Graph f ' (x) and it's derivative f '' (x)
b) On which intervals is f concave up?

16. Given a function with it's derivative defined as:
f ' (x) = (ln x)2 ­ 2(sinx)2 for 0 < x < 6
Graph f ' (x) and it's derivative f '' (x)
c) Given f (0.1) = 0, sketch a possible graph of f

17. Exercise 2.6
Questions 5, 7, 15, 17, and 19