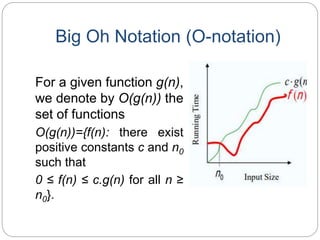
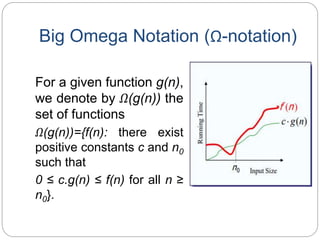
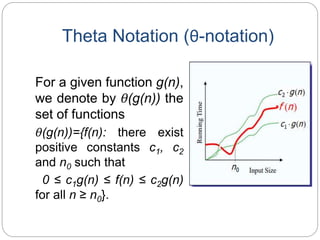
This document defines and explains asymptotic notations used to analyze the time complexity of algorithms. It discusses Big-O, Big-Omega, Theta, Little-o and Little-Omega notations. Big-O notation expresses the upper bound of an algorithm's running time and measures worst case time complexity. Big-Omega notation expresses the lower bound and measures best case time complexity. Theta notation represents both the upper and lower bounds and is used for average case analysis. Examples are provided to demonstrate how functions are bounded using these notations.

1. By: Alisha Jindal
Asymptotic Notations

2. Definition
 Finite sequence of logically related
instructions to solve a computational problem
 Expressions that are used to represent the
complexity of an algorithm
 Describes the behavior of time and space
complexity for large instance characteristics
and ignore for small values
 Using asymptotic analysis, we can conclude
best case, average case and worst case
scenario of an algorithm.

3. Types of Asymptotic Notations
Notations used in calculating running time
complexity of an algorithm:
 Big Oh Notation (O)
 Big Omega Notation (Ω)
 Theta Notation (θ)
 Little Oh Notation (o)
 Little Omega Notation (ω)

4. Big Oh Notation (O-notation)
 It expresses the upper bound of an
algorithm’s running time.
 It measures the worst case time
complexity or maximum amount of time an
algorithm can take to complete.
 It is used as a tight upper-bound on
growth of algorithm

5. Big Oh Notation (O-notation)
For a given function g(n),
we denote by O(g(n)) the
set of functions
O(g(n))={f(n): there exist
positive constants c and n0
such that
0 ≤ f(n) ≤ c.g(n) for all n ≥
n0}.

6. Examples
Show that the function is tightly bound with
big oh notation
(a) f(n)=3n+5
(b) f(n)= 27n2+16n
(c) f(n) = 2n +6n2 + 3n

7. Solutions
(a) 3n+5 ≤ 3n+n ≤ 4n (c=4, n0 =5)
So, f(n)= O(n)
(b) As n2≥ 16n,
27n2 + 16n ≤ 27n2 + n2 ≤ 28n2 (c=28, n0
=16)
So, f(n)=O(n2)
(c) As n2≥ 3n
2n +6n2+3n ≤ 2n +6n2+n2 ≤ 2n +7n2
As 2n ≥ n2 (n ≥ 4)
2n +7n2 ≤ 2n +7*2n ≤ 8*2n (c=8, n0 =4)
So, f(n)=O(2n)

8. Asymptotic Analysis of Running
Time
Comparing running time
 Algorithm that runs in O(n) time is better
than the algorithm that takes O(n2) time
 Similarly, O(log n) is better than O(n)
 Hierarchy of functions:
1< log n < n < nlogn < n2 < n3 < 2n

9. Big Omega Notation (Ω-notation)
 It expresses the lower bound of an
algorithm’s running time.
 It measures the best case time complexity
or minimum amount of time an algorithm
can take to complete.
 It is used as a tight lower-bound on
growth of algorithm

10. Big Omega Notation (Ω-notation)
For a given function g(n),
we denote by Ω(g(n)) the
set of functions
Ω(g(n))={f(n): there exist
positive constants c and n0
such that
0 ≤ c.g(n) ≤ f(n) for all n ≥
n0}.

11. Theta Notation (θ-notation)
 It encloses the function from above and
below. Since it represents the upper and
lower bound of an algorithm’s running
time.
 It is used for analyzing the average case
time complexity of an algorithm

12. Theta Notation (θ-notation)
For a given function g(n),
we denote by θ(g(n)) the
set of functions
θ(g(n))={f(n): there exist
positive constants c1, c2
and n0 such that
0 ≤ c1g(n) ≤ f(n) ≤ c2g(n)
for all n ≥ n0}.

13. Little-Oh Notation (o-notation)
 The functions in o(g) are the smaller
function in O(g)
 It is not asymptotically tight upper-bound
 We define o(g(n)) as the set
o(g(n))={f(n): there exist positive
constants c and n0 such that 0 ≤ f(n) <
cg(n) for all n ≥ n0}

14. Little-Omega Notation (ω-
notation)
 The functions in ω(g) are the larger
function of Ω(g)
 It is not asymptotically tight lower-bound
 We define ω(g(n)) as the set
ω(g(n))={f(n): there exist positive
constants c and n0 such that 0 ≤ cg(n) <
f(n) for all n ≥ n0}

15. Analogy between functions
Comparison of two functions f and g and
comparison of two real numbers a and b:
f(n) = O(g(n)) ≅ a≤b
f(n) = Ω(g(n)) ≅ a≥b
f(n) = θ(g(n)) ≅ a=b
f(n) = o(g(n)) ≅ a<b
f(n) = ω(g(n))≅ a>b