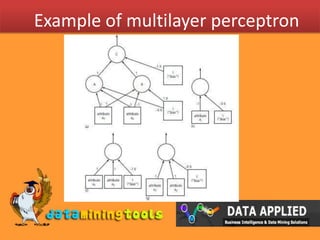
Perceptrons can perform linear classification by using hyperplanes to divide instances belonging to different classes in instance space. Multilayer perceptrons can approximate arbitrary target concepts by creating a network of perceptrons with an input, hidden, and output layer, with the structure found through experimentation. When using montecarlo simulations to determine parameters that minimize the error metric of 1/2(y-f(x))^2, random weight vectors are distributed and sampled to choose those that minimize errors, repeating until convergence to the optimal parameter values.

1. 5 Data-Applied.com: Forecast

2. PerceptronPerceptron can be used for linear classificationLinear classification using the perceptronIf instances belonging to different classes can be divided in the instance space by using hyper planes, then they are called linearly separableIf instances are linearly separable then we can use perceptron learning rule for classification

3. Multilayer PerceptronMultilayer perceptron:We can create a network of perceptron to approximate arbitrary target concepts Multilayer perceptron is an example of an artificial neural networkConsists of: input layer, hidden layer(s), and output layer Structure of MLP is usually found by experimentationParameters can be found using back propagation or montecarlo simulations

4. Example of multilayer perceptron

5. Error metricThe parameters to be selected such that the minimum error is producedError metric used:f(x) = 1/(1+exp(-x))Error = ½(y-f(x))^2

6. Using montecarlo to get the parametersDistribute some random samples in the weight vector spaceChoose the ones which minimizes errorsRepeat the process till convergenceFinally points at the convergence gives us the value of the parameters

7. Forecasts using Data Applied’s web interface

8. Step1: Selection of data

9. Step2: Selecting Forecasts

10. Step3: Result

11. Visit more self help tutorialsPick a tutorial of your choice and browse through it at your own pace.