1. 5. Kernel methods for vector data (II)
e e et ods o ecto ( )
Akisato Kimura (Twitter ID: @_akisato)

2. 初めての方もいらっしゃるので…
初めての方もいらっしゃるので
 Social mediaでの自己紹介
 これまでに関わった研究業界を国内研究会名で書くと
 本業的： IEICE-PRMU, IEICE-IT, SITA, IEICE-IBISML
 副業的： IEICE-DE, ASJ, VSJ, IPSJ-SIGMUS
 これから？： NLP, IPSJ-SIGDIAL
2 CV勉強会 2011.2.19

3. Contents
1. Kernel PCA
 多くのページがここに割かれています
2. FDA / CCA / Subspace methods
3. Manifold learning
 ここまで手が回らなかったので、勘弁して下さい。
【注意】
教科書と全然違うストーリーで説明しています。
記号は合わせてありますが、ご注意下さい。
記号は合わせてありますが ご注意下さい
Cf. 赤穂 “カーネル多変量解析”、岩波書店
3 CV勉強会 2011.2.19

4. 5.1 Kernel PCA

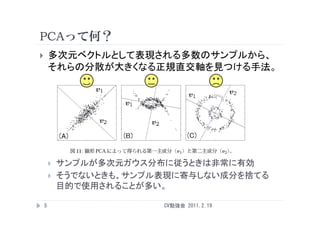
5. PCAって何？
 多次元ベクトルとして表現される多数のサンプルから、
それらの分散が大きくなる正規直交軸を見つける手法。
 サンプルが多次元ガウス分布に従うときは非常に有効
 そうでないときも、サンプル表現に寄与しない成分を捨てる
目的で使用されることが多い。
5 CV勉強会 2011.2.19

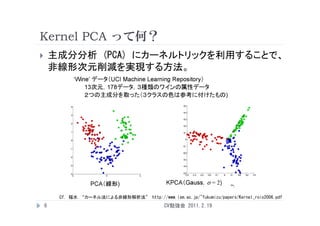
6. Kernel PCA って何？
 主成分分析 (PCA) にカーネルトリックを利用することで、
非線形次元削減を実現する方法。
Cf. 福水 “カーネル法による非線形解析法” http://www.ism.ac.jp/~fukumizu/papers/Kernel_rois2006.pdf
6 CV勉強会 2011.2.19

7. PCAの定式化 １
 多次元ベクトルのサンプルが与えられているとする。
 簡単のため、以降はサンプル平均=0であることを仮定します。
要注意 （教科書に合わせています）
 射影後のサンプルの分散が最大になる基底 を求める
7 CV勉強会 2011.2.19

8. PCAの定式化 ２
 各基底が単位ベクトルとなるように正規化
 Lagrange 未定定数法を用いて、問題を書き直す。
 基底での微分=0 とすると、
 共分散行列の固有値問題を解けば良い！
8 CV勉強会 2011.2.19

9. PCAにおける基底の選択
 PCAの目的関数に固有値問題の解を導入すると
 固有値＝射影後のサンプルの分散
→ 固有値が大きい順に対応する固有ベクトルを基底とする
 寄与率・累積寄与率
 寄与率
寄与率： 所定の基底が表現できるサンプルの分散
（第 i 番目の基底の寄与率）
（第 i 番目までの基底の累積寄与率）
9 CV勉強会 2011.2.19

10. PCAによる次元削減
 新しいサンプル を、選択された基底群で決まる
部分空間に（直交）射影する。
 要するに、サンプルと各基底との内積を取れば良い。
 寄与率を考慮した射影を考える場合もある。
10 CV勉強会 2011.2.19

11. PCA to Kernel PCA
 見かけ上は、非常に簡単に移行できます。
1. グラム行列を構成し、その固有値問題を解く。
2.
2 新しいサンプルと得られた固有ベクトルとの
（カーネルで規定される空間上で）内積を取る。
 …ですが、何でそうなるのか？
 ということについて、これから説明します。
う 、 説明 す。
11 CV勉強会 2011.2.19

12. Kernel PCAの定式化 １
 まず、サンプルを非線形変換する
 言うまでもないですが、実際には計算できない変換です。
 ここでも同様に、（変換後）サンプル平均=0を仮定します。
 射影後のサンプルの分散が最大になる基底 を求める
12 CV勉強会 2011.2.19

13. Kernel PCAの定式化 ２
 各基底が単位ベクトルとなるように正規化
 Lagrange 未定定数法を用いて 問題を書き直す
未定定数法を用いて、問題を書き直す。
 基底での微分を取ると
共分散行列を計算できない！
 共分散行列の固有値問題を…というわけにはいかない。
13 CV勉強会 2011.2.19

14. Kernel PCAの定式化 ３
 もう少し詳しく見てみよう
 ゆえに、新しいサンプルの部分空間への射影は
ゆえに 新しいサンプルの部分空間への射影は
グラム行列で計算できる！
14 CV勉強会 2011.2.19

15. Kernel PCAの定式化 ４
 あとは係数 v をどう求めるか？ が課題。
 もう一度、射影後のサンプルの分散を計算してみる。
15 CV勉強会 2011.2.19

16. Kernel PCAの定式化 ５
 各基底が単位ベクトルとなるように正規化
 Lagrange 未定定数法を用いて 問題を書き直す
未定定数法を用いて、問題を書き直す。
 基底での微分を取ると、
 （グラム行列が正則であれば）
グラム行列の固有値問題を解けば、基底が求まる！
16 CV勉強会 2011.2.19

17. Kernel PCAを行った例 １
 多項式カーネル（次数=3）を用いた場合
17 CV勉強会 2011.2.19

18. Kernel PCAを行った例 ２
 ガウスカーネル（σ=40）を用いた場合
18 CV勉強会 2011.2.19

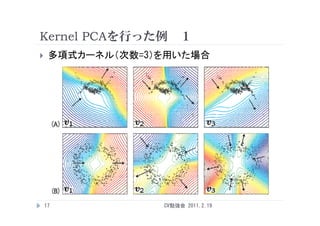
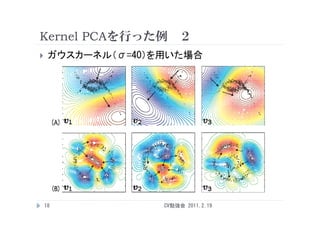
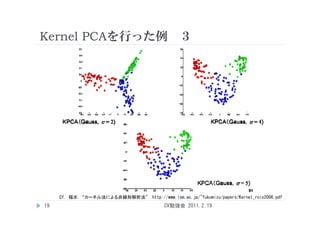
19. Kernel PCAを行った例 ３
Cf. 福水 “カーネル法による非線形解析法” http://www.ism.ac.jp/~fukumizu/papers/Kernel_rois2006.pdf
19 CV勉強会 2011.2.19

20. Kernel PCAの問題点
 結果はカーネルの選び方に大きく依存する。
 どんな種類のカーネルを使うか？パラメータは？
 ガウスカーネルの場合には，分散パラメータを
自動的に選択する方法がいくつか提案されている．
自動的 選択する方法が く か提案され る
 （Mean shiftの節などを参照．）
 しかし、カーネルの選び方に確固たる方法論はない。
 どのような目的・応用に用いられるか？ で異なる
で異なる。
 つまりは、その目的・応用で良い結果が得られるかどうか？
が、カ ネルを選択するための現時点で最良の方法
が、カーネルを選択するための現時点で最良の方法
20 CV勉強会 2011.2.19

21. 5.2 FDA / CCA / Subspace methods
CC et ods

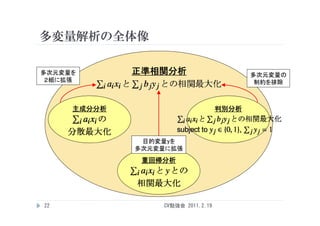
22. 多変量解析の全体像
多次元変量を 正準相関分析 多次元変量の
２組に拡張 制約を排除
主成分分析 判別分析
目的変量yを
的変量 を
多次元変量に拡張
重回帰分析
22 CV勉強会 2011.2.19

23. 正準相関分析 (CCA)
 2組の多次元ベクトル群が与えられているとする。
※ 簡単のため平均０を仮定します。
 このベクトル群を個別に射影するための基底を求めたい。
 基準： 射影後のサンプル群の正規化相関が最大になる基底
Cf. @_akisato “正準相関分析” http://www.slideshare.net/akisatokimura/090608-cca
23 CV勉強会 2011.2.19

24. CCAの定式化 １
 各変換を以下のようにして正規化
 正規化の意味： 変換先の変量を標準正規化する
 Lagrange未定定数法を用いて、問題を書き直す。
 各変換で微分すると・・・
24 CV勉強会 2011.2.19

25. CCAの定式化 ２
 共分散行列 が正則であるとすると、
下記の一般化固有値問題に変形可能
4
 共分散行列のCholesky分解を用いることで、
通常の固有値問題に変形可能 下三角行列
2
1
3
25 CV勉強会 2011.2.19

26. CCAの特殊例
 CCAを特殊化することで、以下のような問題も解けます。
 Fisher線形判別分析 (FDA)
 CCAをマルチラベル分類と考えたときの、シングルラベル版。
：クラス間分散 ：クラス内分散
 線形回帰分析（重回帰分析: MLR）
 通常は最小自乗法で求めるが、
一般化固有値問題として解くこともできる。
Cf. 木村+“拡張ペアワイズ表現を用いた一般化多変量解析” to appear in MIRU2011
26 CV勉強会 2011.2.19

27. Kernel CCA
 Kernel CCAの導出もPCAとほぼ同様にできる。
 PCA同様，形式的には共分散行列をグラム行列で置換．
 正則化が事実上必須．
 グラム行列のランクが元の次元数しかなく，解が安定しない．
Tikhonov正則化 （L2ノルム正則化）
Cf. Max Welling “Kernel canonical correlation analysis”, http://ow.ly/3ZtZ3
27 CV勉強会 2011.2.19

28. 5.3 Manifold learning

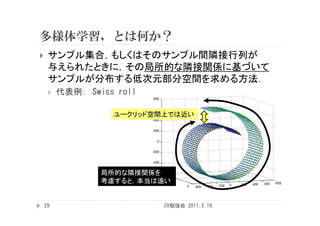
29. 多様体学習，とは何か？
多様体学習 とは何か？
 サンプル集合，もしくはそのサンプル間隣接行列が
与えられたときに，その局所的な隣接関係に基づいて
サンプルが分布する低次元部分空間を求める方法．
 代表例： Swiss roll
ユークリッド空間上では近い
ユ クリッド空間上では近い
局所的な隣接関係を
考慮すると，本当は遠い
29 CV勉強会 2011.2.19

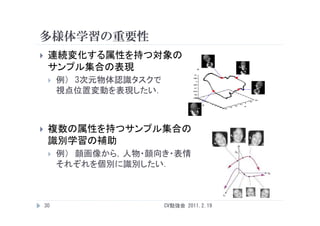
30. 多様体学習の重要性
 連続変化する属性を持つ対象の
サンプル集合の表現
 例） 3次元物体認識タスクで
視点位置変動を表現したい．
視点位置変動を表現したい
 複数の属性を持つサンプル集合の
識別学習の補助
 例） 顔画像から，人物・顔向き・表情
それぞれを個別に識別したい．
それぞれを個別に識別したい
30 CV勉強会 2011.2.19

31. これってkernel PCAじゃないの？
 原空間における非線形基底を求めているのと同じ
 だが，どのようにカーネルを設計すれば
所望の多様体を獲得できるのかがわからない．
 （でも実際にはkernel PCAの特殊例になるんですが…）
31 CV勉強会 2011.2.19

32. 代表的な多様体学習のための手法 (1)
 Isomap [Tenenbaum+ 2000]
 Isomap Homepage: http://isomap.stanford.edu
スパースな隣接行列を作る
＝サンプルを頂点に対応づける
サンプルを頂点に対応づける
グラフを作る
グラフ上の各頂点間の最短
パスを見つけ，その距離を
新しい隣接行列と考える．
（変換した）新しい隣接行列の
固有ベクトルが，埋め込み先の
基底となる．
基底となる
32 CV勉強会 2011.2.19

33. 代表的な多様体学習のための手法 (2)
 Local Linear Embedding (LLE) [Roweis+ 2000]
 LLE page: http://ow.ly/4FsVz
所定数の近傍サンプルを取り出す
近傍サンプルのみから共分散行列を
計算し，それに基づいて重み付け
重み行列の固有ベクトルが
埋め込み先の基底となる
33 CV勉強会 2011.2.19

34. 実は全部kernel PCAと見なせます
 が，それは文献 [27] を見て下さい．
 （実は間に合わなかっただけ）
34 CV勉強会 2011.2.19

35. おしまい
35 CV勉強会 2011.2.19