(1) Current shaping strategies for buck power factor correction converters are discussed. (2) Sine-squared modulation is analyzed where the average inductor current is shaped to follow a sine-squared waveform to improve the power factor. (3) The K-value, which determines the conduction angle and power factor, is analyzed and its impact on the harmonic content of the input current is shown, with various harmonics either meeting or violating Class C and Class D emission standards based on the K-value.





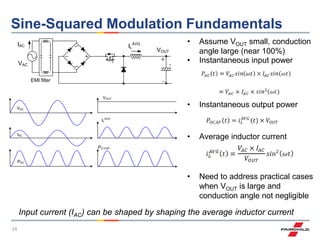
![7
Harmonics Review
1
1
( ) sin( ) :
( ) sin( )n n
n
V t V t Pure AC voltage
i t I nt
Load
i(t)
v(t)
0
10
1
1
( ) ( ) ( )
1
{ sin( )[ sin( )]}
T
av
T
n n
n
P t v t i t dt
T
V t I nt dt
T
1 1
1( ) cos( )
2
av
V I
P t
Harmonic currents from an energy transfer point of view
Net energy is transmitted to the load only when the Fourier Series of v(t) and
i(t) contains terms at the same frequency
For a sinusoidal voltage v(t), harmonics of i(t) are not involved in energy
transfer (just circulating)
0
sin( )sin( ) 0 ( 1)
T
nt nt dt if n ](https://image.slidesharecdn.com/27ad7798-49f2-4590-a71b-f290d1ecb4a7-150818022636-lva1-app6892/85/Current_Shap_Strat_Buck_PFC-7-320.jpg)