Cuda 2011

Agenda for Today Introduction to CUDA Memory architecture Host-GPU workload partitioning and mapping Suitable applications Programming paradigm Lab exercises Hello World Matrix multiplication Numerical computation of pi Parallel sort Copyright © 2011 4-

General Purpose GPU Highly parallel, Multithreaded, Many-core processor Very high memory bandwidth More Transistors for Data Processing Data parallel algorithms leverage GPU attributes Fine-grain SIMD parallelism Low-latency floating point (FP) computation Copyright © 2011 4- GeForce 8800 Tesla S870 Tesla D870

CUDA Compute Unified Device Architecture Introduced by NVIDIA in November 2006 A general purpose parallel computing architecture with A new parallel programming model A New instruction set architecture Three key abstractions A hierarchy of thread groups Shared memories Barrier synchronization CUDA provides A minimal set of language extensions Fine-grained data & thread parallelism nested within coarse-grained data & task parallelism Copyright © 2011 4-

Task Decomposition Partition the problem into coarser and independent sub-problems Partition independent sub-problems into cooperative finer pieces Threads cooperate when solving each sub-problem Each sub-problem can be scheduled to any available core Compiled CUDA program can execute on any number of cores Only runtime system needs to know actual No. of cores Copyright © 2011 4-

Benefits Just parallelize the task parallelization Don’t worry about implementation Support heterogeneous computation Applications use both the CPU and GPU Serial portions on the CPU Parallel portions offloaded to GPU Simultaneous computation on CPU and GPU No memory contention between CPU & GPU assigned code CUDA can be incrementally applied to existing applications CUDA-capable GPUs Hundreds of cores Run thousands of computing threads Reduces system memory bus traffic Copyright © 2011 4-

Kernels Functions written in C for CUDA using __global__ declaration specifier Executed N times in parallel by N different CUDA threads Number of CUDA threads for each call is specified using a new <<<…>>> syntax // Kernel definition __global__ void VecAdd(float* A, float* B, float* C){ //device code here } int main(){ //Host code here VecAdd<<<1, N>>>(A, B, C); // Kernel invocation } Copyright © 2011 4-

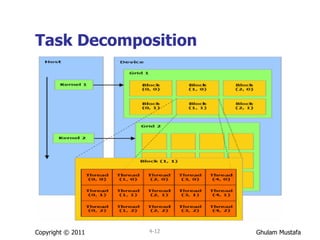
Threads within kernel Each thread of kernel is given a unique thread ID Accessible within the kernel via built-in variable threadIdx // Kernel definition __global__ void VecAdd(float* A, float* B, float* C){ int i = threadIdx.x; //Each threads performs one pair-wise addition C[i] = A[i] + B[i]; } int main(){ // Kernel invocation VecAdd<<<1, N>>>(A, B, C); } Copyright © 2011 4-

Thread IDs threadIdx is a 3-component vector Threads can be identified using a 1-D, 2-D & 3-D thread index Allows the formation of 1-D, 2-D or 3-D thread blocks A natural way to invoke computation across the elements in a vector, matrix, or field For a 2-D block of size (Dx, Dy) Thread ID of a thread of index (x, y) is (x + y Dx) For a 3-D block of size (Dx, Dy, Dz) Thread ID of a thread of index (x, y, z) is (x + y Dx + z Dx Dy) For a 1-D block, they are the same Copyright © 2011 4-

Thread synchronization Threads within a block cooperate by sharing data through shared memory Intrinsic function __syncthreads() used as barrier Acts as synchronization point Shared memory is expected to be Low-latency memory Near each processor core Like an L1 cache __syncthreads() is expected to be Lightweight All threads of a block reside on the same processor core #Threads per block is restricted by the limited memory resources of a processor core On current GPUs, a thread block may contain up to 512 threads Copyright © 2011 4-

Thread Blocks (1/2) Kernel can be executed by multiple equally-shaped thread blocks Total #threads = (#threads per block) x (#blocks) Multiple blocks are organized into 1-D or 2-D Grid of blocks Dimension of grid is specified by first parameter of the <<<…>>> Each block within the grid can be identified by a 1-D or 2-D index Block within a kernel is accessible via built-in variable blockIdx Block dimension is accessible within the kernel via built-in variable blockDim Copyright © 2011 4-

Thread Blocks (2/2) Thread blocks can be scheduled in any order across any number of cores Enables programmers to write code that scales with the number of cores #thread blocks in a grid is dictated by the size of the data being processed not by #processors in the system Copyright © 2011 4-

Example // Kernel definition __global__ void MatAdd(float A[N][N], float B[N][N], float C[N][N]){ int i = blockIdx.x * blockDim.x + threadIdx.x; // x + y Dx int j = blockIdx.y * blockDim.y + threadIdx.y; // y + x Dy if (i < N && j < N) C[i][j] = A[i][j] + B[i][j]; } int main(){ // Kernel invocation dim3 dimBlock(16, 16); //16x16=256 threads dim3 dimGrid((N + dimBlock.x – 1) / dimBlock.x, (N + dimBlock.y – 1) / dimBlock.y); MatAdd<<<dimGrid, dimBlock>>>(A, B, C); } Copyright © 2011 4-

Programming Interface Two mutually exclusive interfaces C for CUDA Any source file that contains some of these extensions must be compiled with nvcc CUDA driver API lower-level C API that provides functions to Load kernels as modules of CUDA binary or assembly code Inspect their parameters Launch them Copyright © 2011 4-

nvcc (1/2) A compiler driver simplifies the compilation CUDA code Provides simple and familiar command line options Invokes a collection of tools that implement the different compilation stages Separates device code from host code Compiles device code into an assembly form ( PTX code) or binary form (cubin object) Generates host code in either C code to be compiled using another tool Object code directly by invoking the host compiler during the last compilation stage Copyright © 2011 4-

nvcc (2/2) Front end of nvcc processes CUDA source code according to C++ syntax rules Full C++ is supported for the host code void pointers cannot be assigned to non-void pointers without a typecast Only C subset of C++ is fully supported for the device code Copyright © 2011 4-

Device Emulation No debugging facility in CUDA Debugging done in device emulation mode Programming with CUDA on systems without Nvidia GPUs utilizes this mode Example $ nvcc –o hello –deviceemu hello_world.cu Copyright © 2011 4-

System Configuration Hardware platform X86 with CUDA in device emulation mode Software environment CUDA SDK version 2.2 CUDA toolkit version 2.2 Programming paradigm specific details…. Data Parallel model Loops are attacked Within a grid, threads synchronized using Barrier (if necessary) Copyright © 2011 4-

HelloWorld Code #include <cuda.h> #include <stdio.h> #include <stdlib.h> __global__ void printhello() { int thid = blockIdx.x * blockDim.x + threadIdx.x; printf("Thread%d: Hello World!\n", thid); } int main() { printhello<<<5,10>>>(); return 0; } Copyright © 2011 4-

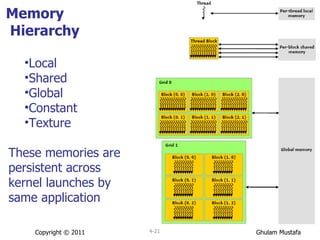
Matrix Multiplication Code (1/5) /* Matrices are stored in row-major order: * M(row, col) = M.ents[row * M.w + col] */ #define BLOCK_SZ 2 #define Xc (2 * BLOCK_SZ) #define Xr (3 * BLOCK_SZ) #define Yc (2 * BLOCK_SZ) #define Yr Xc #define Zc Yc #define Zr Xr typedef struct Matrix{ int r,c; float* elements; } matrix; void populate_matrix(matrix*); void print_matrix(matrix); Copyright © 2011 4-

Matrix Multiplication Code (2/5) __global__ void matrix_mul_krnl(matrix A, matrix B, matrix C) { float C_entry = 0; int row = blockIdx.y * blockDim.y + threadIdx.y; int col = blockIdx.x * blockDim.x + threadIdx.x; int i; for (i = 0; i < A.c; i++) C_entry += A.elements[row * A.c + i] * B.elements[i * B.c + col]; C.elements[row * C.c + col] = C_entry; } Copyright © 2011 4-

Matrix Multiplication Code (3/5) int main() { matrix X, Y, Z; X.r = Xr; Y.r = Yr; Z.r = Zr; X.c = Xc; Y.c = Yc; Z.c = Zc; printf("C(%d,%d) = A(%d,%d) x B(%d,%d)\n” ,Z.r,Z.c, X.r,X.c, Y.r,Y.c); size_t size_Z = Z.c * Z.r * sizeof(float); Z.elements = (float*) malloc(size_Z); populate_matrix(&X); populate_matrix(&Y); print_matrix(X); print_matrix(Y); matrix d_A; d_A.c = X.c; d_A.r = X.r; size_t size_A = X.c * X.r * sizeof(float); cudaMalloc((void**)&d_A.elements, size_A); cudaMemcpy(d_A.elements, X.elements, size_A, cudaMemcpyHostToDevice); Copyright © 2011 4-

Matrix Multiplication Code (4/5) matrix d_B; d_B.c = Y.c; d_B.r = Y.r; size_t size_B = Y.c * Y.r * sizeof(float); cudaMalloc((void**)&d_B.elements, size_B); cudaMemcpy(d_B.elements, Y.elements, size_B,cudaMemcpyHostToDevice); matrix d_C; d_C.c = Z.c; d_C.r = Z.r; size_t size_C = Z.c * Z.r * sizeof(float); cudaMalloc((void**)&d_C.elements, size_C); dim3 dimBlock(BLOCK_SZ, BLOCK_SZ); dim3 dimGrid(Y.c / dimBlock.x, X.r / dimBlock.y); matrix_mul_krnl<<<dimGrid, dimBlock>>>(d_A, d_B, d_C); cudaMemcpy(Z.elements, d_C.elements, size_C, cudaMemcpyDeviceToHost); cudaFree(d_A.elements); cudaFree(d_B.elements); cudaFree(d_C.elements); print_matrix(Z); free (X.elements); free(Y.elements); free(Z.elements); } Copyright © 2011 4-

Matrix Multiplication Code (5/5) void populate_matrix(matrix* mat){ int dim = mat -> c * mat -> r; size_t sz = dim * sizeof(float); mat -> elements = (float*) malloc(sz); int i; for (i = 0; i < dim; i++) mat->elements[i] = (float)(rand()%1000); } void print_matrix(matrix mat){ int i, n = 0, dim; dim = mat.c * mat.r; for (i = 0; i < dim; i++) { if (i == mat.c * n){ printf("\n"); n++; } printf("%0.2f\t", mat.elements[i]); } } Copyright © 2011 4-

Computation of pi Code (2/4) __global__ void calculate_PI(data d, float* s){ float sum, x, w; int itr,i,j; itr = d.PerThrItr; i = blockIdx.x * blockDim.x + threadIdx.x; int N = d.n-i; w = 1.0/(float)N; sum = 0.0; if (i < d.nThr) { for (j = i * itr; j < (i * itr+itr); j++) { x = w * (j-0.5); sum+= (4.0)/(1.0 + x*x); } s[i] = sum * w; } } Copyright © 2011 4-

Computation of pi Code (3/4) int main(int argc, char** argv){ if(argc < 2){ printf("Usage: ./<progname> #itrations #Threads\n"); exit(1); } data pi_data; float PI=0.0; pi_data.n = atoi(argv[1]); pi_data.nThr = atoi(argv[2]); pi_data.PerThrItr = pi_data.n/pi_data.nThr; float *d_sum; float *h_sum; size_t size = pi_data.nThr * sizeof(float); cudaMalloc((void**)&d_sum, size); h_sum = (float*) malloc(size); Copyright © 2011 4-

Computation of pi Code (4/4) int threads_per_block = 4; int blocks_per_grid; blocks_per_grid = (pi_data.nThr + threads_per_block - 1)/threads_per_block; calculate_PI<<<blocks_per_grid,threads_per_block>>>(pi_data, d_sum); cudaMemcpy(h_sum, d_sum, size, cudaMemcpyDeviceToHost); int i; for (i = 0; i < pi_data.nThr; i++) PI+= h_sum[i]; printf("Using %d itrations, Value of PI is %f \n", pi_data.n, PI); cudaFree(d_sum); } Copyright © 2011 4-

Bitonic Sort Sorting network is a sorting algorithm Sequence of comparisons is not data-dependent Suitable for parallel implementations Bitonic sort is one of fastest sorting networks o(n log 2 n) comparators Very efficient when sorting a small number of elements Specially design for parallel machines Copyright © 2011 4- http://www.tools-of-computing.com/tc/CS/Sorts/bitonic_sort.htm

Bitonic Sort All elements Sorted single element subsequences Pairs of elements Sorted in ascending or descending subsequences Elements differing in bit 0 (lowest) are compared and exchanged conditionally If (bit 1 is zero) elements are sorted in ascending order If(bit 1 is 1) Elements are sorted in descending order Copyright © 2011 4- Index 0 1 2 3 4 5 6 7 Binary Form 0000 0001 0010 0011 0100 0101 0110 0111 [0000 , 0001] ascending [0010 , 0011] descending [0100 , 0101] ascending [0110 , 0111] descending

Bitonic Sort k = Bit position to determine swap ascending or descending order j = Distance b/w elements to be compared and conditionally swapped i = Goes through all the elements ixj = exclusive-or of i and j i.e. element whose position differs only in bit position (log 2 j) ixj is the pair of i We only compare elements i and ixj if i<ixj To avoid duplicate comparison Copyright © 2011 4-

Bitonic Sort int i,j,k; for (k=2;k<=N;k=2*k) { for (j=k/2;j>0;j=j/2) { for (i=0;i<N;i++) { int ixj=i^j; if ((ixj)>i) { if ((i&k)==0 && get(i)>get(ixj)) swap(i,ixj); if ((i&k)!=0 && get(i)<get(ixj)) swap(i,ixj); } } } } Copyright © 2011 4-

Parallel Sort Code (1/3) #define NUM 32 __device__ inline void swap(int & a, int & b){ int tmp = a; a = b; b = tmp; } __global__ static void bitonicSort(int * values){ extern __shared__ int shared[]; const unsigned int tid = threadIdx.x; shared[tid] = values[tid]; __syncthreads(); Copyright © 2011 4-

// Parallel bitonic sort for (unsigned int k = 2; k <= NUM; k *= 2) { // Bitonic merge: for (unsigned int j = k / 2; j>0; j /= 2) { unsigned int ixj = tid ^ j; if (ixj > tid){ if ((tid & k) == 0) { if (shared[tid] > shared[ixj]) swap(shared[tid], shared[ixj]); } else{ if (shared[tid] < shared[ixj]) swap(shared[tid], shared[ixj]); } } __syncthreads(); } } // Write result. values[tid] = shared[tid]; } Parallel Sort Code (2/3) Copyright © 2011 4-

Parallel Sort Code (3/3) int main(int argc, char** argv){ int values[NUM]; for(int i = 0; i < NUM; i++) values[i] = rand()%1000; int * dvalues; cudaMalloc((void**)&dvalues, sizeof(int) * NUM); cudaMemcpy(dvalues, values, sizeof(int) * NUM,cudaMemcpyHostToDevice); bitonicSort<<<1, NUM, sizeof(int) * NUM>>>(dvalues); cudaMemcpy(values, dvalues, sizeof(int) * NUM,cudaMemcpyDeviceToHost); cudaFree(dvalues); bool passed = true; int i; for( i = 1; i < NUM; i++) { if (values[i-1] > values[i]) passed = false; } printf( "Test %s\n", passed ? "PASSED" : "FAILED"); } Copyright © 2011 4-

Cuda 2011

More Related Content

What's hot

Similar to Cuda 2011

More from coolmirza143

Recently uploaded

Cuda 2011