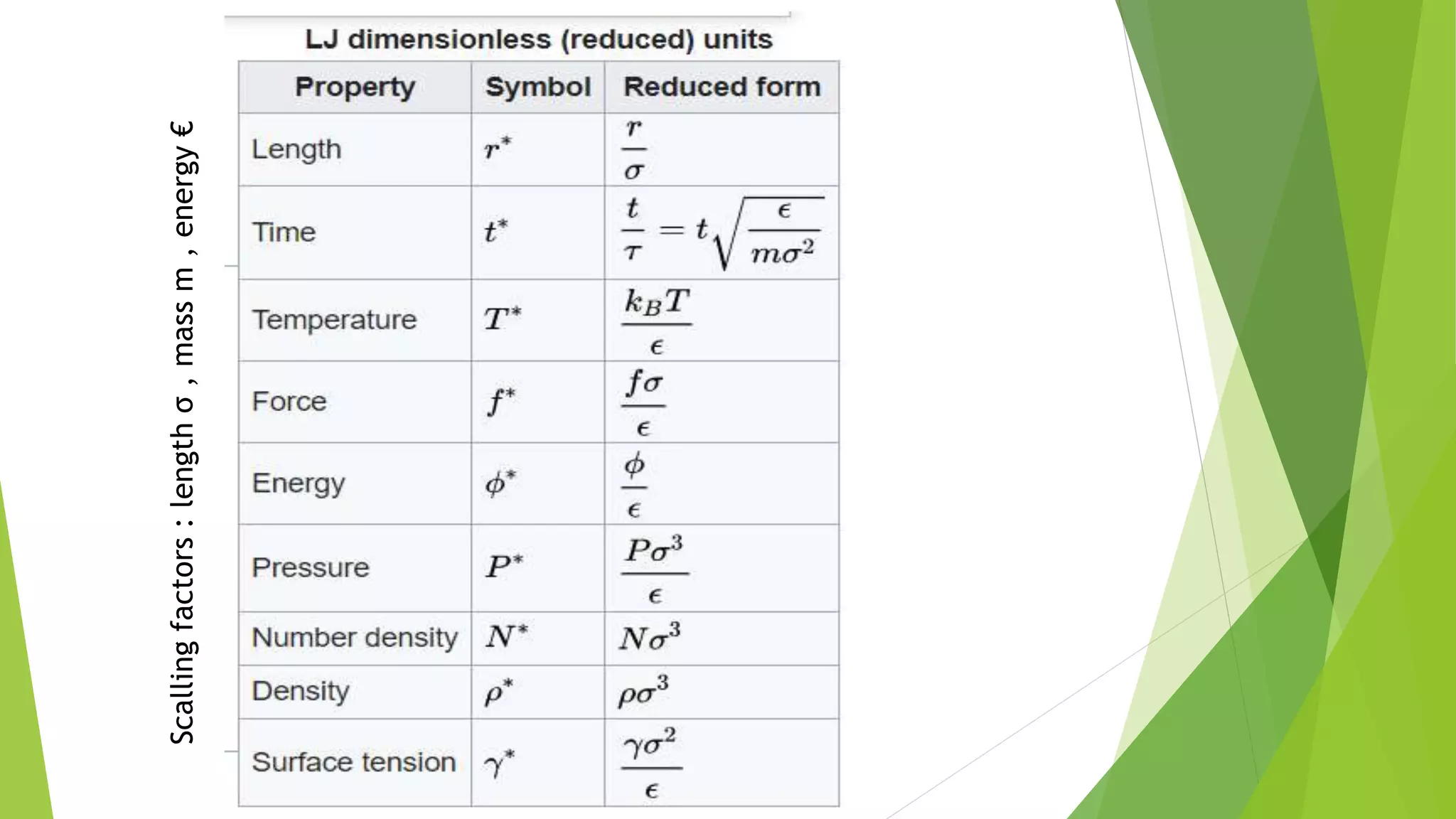
The document discusses the Lennard-Jones potential model for describing interactions between atoms or molecules. It consists of two terms: an attractive dispersion term proportional to 1/R6 representing van der Waals forces, and a repulsive term proportional to 1/R12 representing Pauli repulsion at short distances. The potential is commonly used to model properties of inert gas crystals and determine their lowest energy configurations. However, it has limitations as it oversimplifies real bonding and does not account for directionality or many-body effects.
origin of quantum physics -
Inadequacy of classical mechanics and birth of QUANTUM PHYSICS
ref: Quantum mechanics: concepts and applications, N. Zettili
origin of quantum physics -
Inadequacy of classical mechanics and birth of QUANTUM PHYSICS
ref: Quantum mechanics: concepts and applications, N. Zettili
Hello, I am Subhajit Pramanick. I and my classmate, Anannya Sahaw, both presented this ppt in seminar of our Institute, Indian Institute of Technology, Kharagpur. The topic of this presentation is on exchange interaction and their consequences. It includes the basic of exchange interaction, the origin of it, classification of it and their discussions etc. We hope you will all enjoy by reading this presentation. Thank you.
Hello, I am Subhajit Pramanick. I and my classmate, Anannya Sahaw, both presented this ppt in seminar of our Institute, Indian Institute of Technology, Kharagpur. The topic of this presentation is on exchange interaction and their consequences. It includes the basic of exchange interaction, the origin of it, classification of it and their discussions etc. We hope you will all enjoy by reading this presentation. Thank you.
This presentation is the introduction to Density Functional Theory, an essential computational approach used by Physicist and Quantum Chemist to study Solid State matter.
7.1 Application of the Schrödinger Equation to the Hydrogen Atom
7.2 Solution of the Schrödinger Equation for Hydrogen
7.3 Quantum Numbers
7.4 Magnetic Effects on Atomic Spectra – The Normal Zeeman Effect
7.5 Intrinsic Spin
7.6 Energy Levels and Electron Probabilities
A Study on Atomic Spectroscopic Term Symbols for Nonequivalent Electrons of (...IJERA Editor
Electronic and magnetic properties of the inorganic molecules and complexes can be understood very well by using the term symbols. Term symbols are a shorthand method used to describe the energy, angular momentum, and spin multiplicity of an atom / ion in any particular electronic state. The Russell-Saunders atomic term symbols provide the information about spectral and magnetic properties of an atom or ion. The atomic terms have been determined for nonequivalent electrons of(n-1)d 1 s 1 p 1 configuration using Russell-Saunders coupling scheme.The total number of microstates computed for the non-equivalent electrons of (n-1)d 1 s 1 p 1 configuration are found to be 120. Among the microstates, two types of atomic terms have been determined namely, quartet (3-types) and doublet (6-types). The ground state term found for this configuration is quartet 4 F with the lower energy state as 4 F2
Paulis principle speectra of alkali atom.pptxjagadis3
In quantum mechanics, the Pauli exclusion principle states that two or more identical particles with half-integer spins (i.e. fermions) cannot occupy the same quantum state within a quantum system simultaneously. This principle was formulated by Austrian physicist Wolfgang Pauli in 1925 for electrons, and later extended to all fermions with his spin–statistics theorem of 1940.
In the case of electrons in atoms, it can be stated as follows: it is impossible for two electrons of a poly-electron atom to have the same values of the four quantum numbers: n, the principal quantum number; ℓ, the azimuthal quantum number; mℓ, the magnetic quantum number; and ms, the spin quantum number. For example, if two electrons reside in the same orbital, then their n, ℓ, and mℓ values are the same; therefore their ms must be different, and thus the electrons must have opposite half-integer spin projections of 1/2 and −1/2The Pauli exclusion principle describes the behavior of all fermions (particles with half-integer spin), while bosons (particles with integer spin) are subject to other principles. Fermions include elementary particles such as quarks, electrons and neutrinos. Additionally, baryons such as protons and neutrons (subatomic particles composed from three quarks) and some atoms (such as helium-3) are fermions, and are therefore described by the Pauli exclusion principle as well. Atoms can have different overall spin, which determines whether they are fermions or bosons: for example, helium-3 has spin 1/2 and is therefore a fermion, whereas helium-4 has spin 0 and is a boson.[1]: 123–125 The Pauli exclusion principle underpins many properties of everyday matter, from its large-scale stability to the chemical behavior of atoms.
Half-integer spin means that the intrinsic angular momentum value of fermions is
ℏ
=
ℎ
/
2
�\hbar = h/2\pi (reduced Planck's constant) times a half-integer (1/2, 3/2, 5/2, etc.). In the theory of quantum mechanics, fermions are described by antisymmetric states. In contrast, particles with integer spin (bosons) have symmetric wave functions and may share the same quantum states. Bosons include the photon, the Cooper pairs which are responsible for superconductivity, and the W and Z bosons. Fermions take their name from the Fermi–Dirac statistical distribution, which they obey, and bosons take theirs from the Bose–Einstein distribution.
History
What is greenhouse gasses and how many gasses are there to affect the Earth.moosaasad1975
What are greenhouse gasses how they affect the earth and its environment what is the future of the environment and earth how the weather and the climate effects.
Seminar of U.V. Spectroscopy by SAMIR PANDASAMIR PANDA
Spectroscopy is a branch of science dealing the study of interaction of electromagnetic radiation with matter.
Ultraviolet-visible spectroscopy refers to absorption spectroscopy or reflect spectroscopy in the UV-VIS spectral region.
Ultraviolet-visible spectroscopy is an analytical method that can measure the amount of light received by the analyte.
Multi-source connectivity as the driver of solar wind variability in the heli...Sérgio Sacani
The ambient solar wind that flls the heliosphere originates from multiple
sources in the solar corona and is highly structured. It is often described
as high-speed, relatively homogeneous, plasma streams from coronal
holes and slow-speed, highly variable, streams whose source regions are
under debate. A key goal of ESA/NASA’s Solar Orbiter mission is to identify
solar wind sources and understand what drives the complexity seen in the
heliosphere. By combining magnetic feld modelling and spectroscopic
techniques with high-resolution observations and measurements, we show
that the solar wind variability detected in situ by Solar Orbiter in March
2022 is driven by spatio-temporal changes in the magnetic connectivity to
multiple sources in the solar atmosphere. The magnetic feld footpoints
connected to the spacecraft moved from the boundaries of a coronal hole
to one active region (12961) and then across to another region (12957). This
is refected in the in situ measurements, which show the transition from fast
to highly Alfvénic then to slow solar wind that is disrupted by the arrival of
a coronal mass ejection. Our results describe solar wind variability at 0.5 au
but are applicable to near-Earth observatories.
THE IMPORTANCE OF MARTIAN ATMOSPHERE SAMPLE RETURN.Sérgio Sacani
The return of a sample of near-surface atmosphere from Mars would facilitate answers to several first-order science questions surrounding the formation and evolution of the planet. One of the important aspects of terrestrial planet formation in general is the role that primary atmospheres played in influencing the chemistry and structure of the planets and their antecedents. Studies of the martian atmosphere can be used to investigate the role of a primary atmosphere in its history. Atmosphere samples would also inform our understanding of the near-surface chemistry of the planet, and ultimately the prospects for life. High-precision isotopic analyses of constituent gases are needed to address these questions, requiring that the analyses are made on returned samples rather than in situ.
Richard's entangled aventures in wonderlandRichard Gill
Since the loophole-free Bell experiments of 2020 and the Nobel prizes in physics of 2022, critics of Bell's work have retreated to the fortress of super-determinism. Now, super-determinism is a derogatory word - it just means "determinism". Palmer, Hance and Hossenfelder argue that quantum mechanics and determinism are not incompatible, using a sophisticated mathematical construction based on a subtle thinning of allowed states and measurements in quantum mechanics, such that what is left appears to make Bell's argument fail, without altering the empirical predictions of quantum mechanics. I think however that it is a smoke screen, and the slogan "lost in math" comes to my mind. I will discuss some other recent disproofs of Bell's theorem using the language of causality based on causal graphs. Causal thinking is also central to law and justice. I will mention surprising connections to my work on serial killer nurse cases, in particular the Dutch case of Lucia de Berk and the current UK case of Lucy Letby.
Nutraceutical market, scope and growth: Herbal drug technologyLokesh Patil
As consumer awareness of health and wellness rises, the nutraceutical market—which includes goods like functional meals, drinks, and dietary supplements that provide health advantages beyond basic nutrition—is growing significantly. As healthcare expenses rise, the population ages, and people want natural and preventative health solutions more and more, this industry is increasing quickly. Further driving market expansion are product formulation innovations and the use of cutting-edge technology for customized nutrition. With its worldwide reach, the nutraceutical industry is expected to keep growing and provide significant chances for research and investment in a number of categories, including vitamins, minerals, probiotics, and herbal supplements.
Richard's aventures in two entangled wonderlandsRichard Gill
Since the loophole-free Bell experiments of 2020 and the Nobel prizes in physics of 2022, critics of Bell's work have retreated to the fortress of super-determinism. Now, super-determinism is a derogatory word - it just means "determinism". Palmer, Hance and Hossenfelder argue that quantum mechanics and determinism are not incompatible, using a sophisticated mathematical construction based on a subtle thinning of allowed states and measurements in quantum mechanics, such that what is left appears to make Bell's argument fail, without altering the empirical predictions of quantum mechanics. I think however that it is a smoke screen, and the slogan "lost in math" comes to my mind. I will discuss some other recent disproofs of Bell's theorem using the language of causality based on causal graphs. Causal thinking is also central to law and justice. I will mention surprising connections to my work on serial killer nurse cases, in particular the Dutch case of Lucia de Berk and the current UK case of Lucy Letby.
Earliest Galaxies in the JADES Origins Field: Luminosity Function and Cosmic ...Sérgio Sacani
We characterize the earliest galaxy population in the JADES Origins Field (JOF), the deepest
imaging field observed with JWST. We make use of the ancillary Hubble optical images (5 filters
spanning 0.4−0.9µm) and novel JWST images with 14 filters spanning 0.8−5µm, including 7 mediumband filters, and reaching total exposure times of up to 46 hours per filter. We combine all our data
at > 2.3µm to construct an ultradeep image, reaching as deep as ≈ 31.4 AB mag in the stack and
30.3-31.0 AB mag (5σ, r = 0.1” circular aperture) in individual filters. We measure photometric
redshifts and use robust selection criteria to identify a sample of eight galaxy candidates at redshifts
z = 11.5 − 15. These objects show compact half-light radii of R1/2 ∼ 50 − 200pc, stellar masses of
M⋆ ∼ 107−108M⊙, and star-formation rates of SFR ∼ 0.1−1 M⊙ yr−1
. Our search finds no candidates
at 15 < z < 20, placing upper limits at these redshifts. We develop a forward modeling approach to
infer the properties of the evolving luminosity function without binning in redshift or luminosity that
marginalizes over the photometric redshift uncertainty of our candidate galaxies and incorporates the
impact of non-detections. We find a z = 12 luminosity function in good agreement with prior results,
and that the luminosity function normalization and UV luminosity density decline by a factor of ∼ 2.5
from z = 12 to z = 14. We discuss the possible implications of our results in the context of theoretical
models for evolution of the dark matter halo mass function.
Observation of Io’s Resurfacing via Plume Deposition Using Ground-based Adapt...Sérgio Sacani
Since volcanic activity was first discovered on Io from Voyager images in 1979, changes
on Io’s surface have been monitored from both spacecraft and ground-based telescopes.
Here, we present the highest spatial resolution images of Io ever obtained from a groundbased telescope. These images, acquired by the SHARK-VIS instrument on the Large
Binocular Telescope, show evidence of a major resurfacing event on Io’s trailing hemisphere. When compared to the most recent spacecraft images, the SHARK-VIS images
show that a plume deposit from a powerful eruption at Pillan Patera has covered part
of the long-lived Pele plume deposit. Although this type of resurfacing event may be common on Io, few have been detected due to the rarity of spacecraft visits and the previously low spatial resolution available from Earth-based telescopes. The SHARK-VIS instrument ushers in a new era of high resolution imaging of Io’s surface using adaptive
optics at visible wavelengths.
8. Total Hamiltonian ,
ℋ = 𝐻0 + 𝐻1
This H can be diagonalised by the Normal Mode
transformation
𝑥 𝑠 =
1
2
𝑥1 + 𝑥2
𝑥 𝑎 =
1
2
𝑥1 − 𝑥2
9. So the modified total Hamiltonian,
𝓗 =
𝒑 𝒔
𝟐
𝟐𝒎
+
𝟏
𝟐
𝒌 −
𝟐𝒆^𝟐
𝑹 𝟑
𝒙 𝒔
𝟐
+
𝒑 𝒂
𝟐
𝟐𝒎
+
𝟏
𝟐
𝒌 +
𝟐𝒆^𝟐
𝑹 𝟑
𝒙 𝒂
𝟐
And we get the two frequencies of the coupled oscillators are ,
𝝎 =
𝒌 ±
𝟐𝒆 𝟐
𝑹 𝟑
𝒎
≈ 𝒘 𝟎 𝟏 ±
𝟐𝒆 𝟐
𝒌𝑹 𝟑
= 𝒘 𝟎 𝟏 ±
𝟏
𝟐
𝟐𝒆 𝟐
𝒌𝑹 𝟑 −
𝟏
𝟖
𝟐𝒆 𝟐
𝒌𝑹 𝟑
𝟐
+ ⋯
10. Because of the interaction the sum is lowered by
∆𝑼 =
𝟏
𝟐
ℏ ∆𝒘 𝒔 + ∆𝒘 𝒂 =-ℏ𝒘 𝟎
𝟏
𝟖
𝟐𝒆 𝟐
𝒌𝑹 𝟑
𝟐
∆𝑼 = −
𝑨
𝑹 𝟔
The Zero Point energy of the system is
U=
𝟏
𝟐
ℏ 𝒘 𝒔 + 𝒘 𝒂
This is known as Van der Waal Interaction or London Interaction
or Dipole-Dipole Interaction .
𝐴 = ℏ𝑤0
𝑒4
2𝑘2
13. The total repulsive term is,
𝑈2 =
𝐵
𝑅12
The Total potential energy of two atoms at separation R is ,
𝑈 𝑅 = −
𝐴
𝑅6 +
𝐵
𝑅12
Where A & B are empirical parameters .
This Potential is known as Lennard-Jones Potential .
14. Curve of Lennard-Jones Potential
U(R)=4∈[ (σ/R)^12 – (σ/R)^6 ]
Where , A = 4∈σ^6 & B = 4∈σ^12
15. Application of Lennard-Jones Potential
:-
Differentiating the L-J Potential w.r.t r gives net
intermolecular force .
It describes the properties of gases and to model dispersion
and overlap interactions in molecular models .
It describes the lowest energy arrangement of infinite
number of atoms .
Dimensionless unit can be defined .
18. Limitations :-
The L-J potential has only two parameters (A and B), which determine the
length and energy scales. The potential is therefore limited in how accurately it
can be fitted to the properties of any real material.
With the L-J potential, the number of atoms bonded to an atom does not affect
bond strength. The bond energy per atom thus rises linearly with the number of
bonds per atom. But experiments show that in real materials, bond energy per
atom rises quadratically with the number of bonds.
The bonding of the L-J potential has no directionality: the potential is
spherically symmetric.
The sixth-power term models effectively the dipole–dipole interactions due to
electron dispersion in noble gases (London dispersion forces), but it does not
represent other kinds of bonding well. The twelfth-power term appearing in the
potential is chosen for its ease of calculation for simulations (by squaring the
sixth-power term) and is not theoretically or physically based.
The potential diverges when two atoms approach one another. This may create
instabilities that require special treatment in molecular dynamics simulations.
