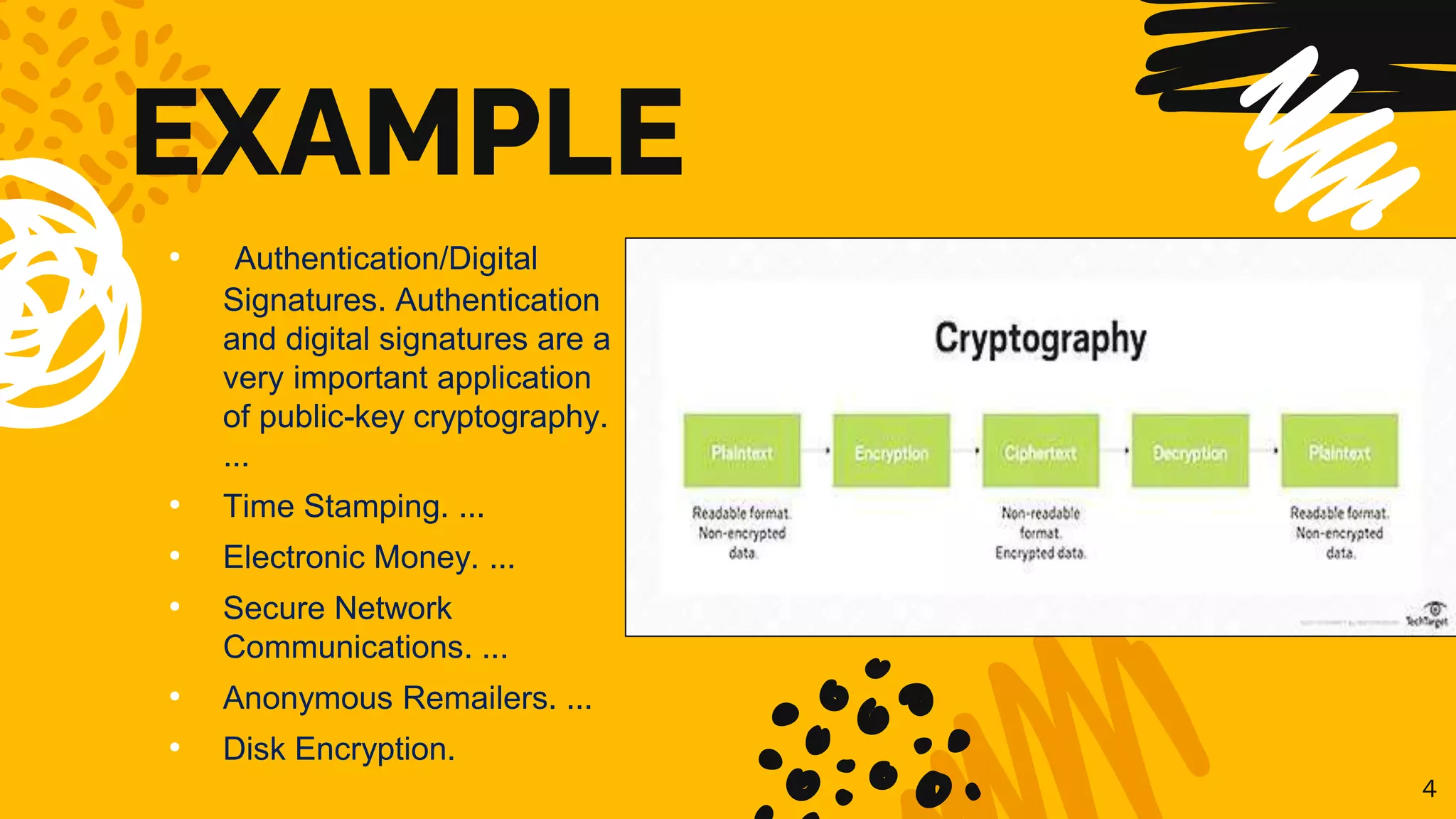
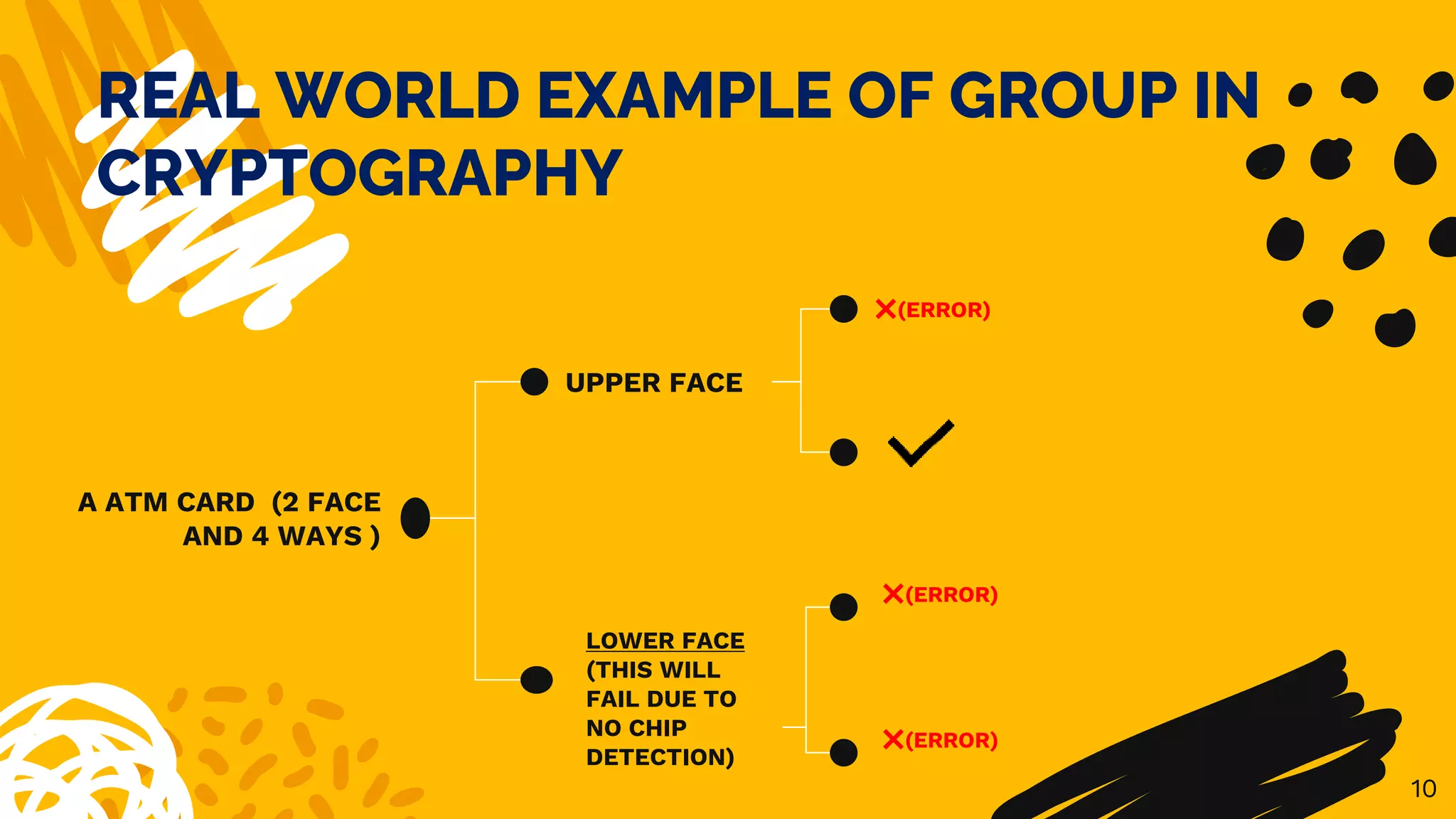
The document discusses the application of group theory in cryptography, particularly focusing on the use of groups for constructing cryptographic protocols. It covers key concepts such as Diffie-Hellman key exchange, the benefits and drawbacks of group-based cryptography, and various real-world applications. Additionally, it emphasizes the role of cyclic groups and nonabelian groups in modern cryptographic methods.

1. IE-MATHS
TOPIC: Application of Groups in
cryptography.
PRESENTED BY ROLL NO
TALHA MOHMIN 33
SUGAM PANDEY 34
ATHARWA PARAB 35
SIMRAN PARDESHI 36

2. Roadmap OF PPT
2
1 3 5
6
4
2
INTRODUCTION Applications
Real world
application
Groups in
cryptography
Adantage and
disadvaantages References

3. WHAT IS CRYPTOGRAPHY ?
✘ Cryptography is technique of securing
information and communications
through use of codes so that only those
person for whom the information is
intended can understand it and process
it. Thus preventing unauthorized access
to information. The prefix “crypt” means
“hidden” and suffix graphy means
“writing”. 3

4. EXAMPLE
• Authentication/Digital
Signatures. Authentication
and digital signatures are a
very important application
of public-key cryptography.
...
• Time Stamping. ...
• Electronic Money. ...
• Secure Network
Communications. ...
• Anonymous Remailers. ...
• Disk Encryption.
4

5. 1. GROUPS IN
CRYPTOGRAPHY

6. GROUPS BASED CRYPTOGRAPHY
✘ Now a days there are various cryptographic protocols
based on groups. The first proposal to use nonabelian
groups in public key cryptograph.
✘ By using Group theory we can construct variants of the
Diffie–Hellman key agreement protocol.
✘ The protocol uses a cyclic subgroup of a finite group G,
one approach is to search for examples of groups that
can be efficiently represented and manipulated.
6

7. APPLICATIONS OF GROUPS
IN CRYPTOGRAPHY
A Group-based cryptography is a use
of groups to construct cryptographic
primitives. A group is a very general
algebraic object and most cryptographic
schemes use groups in some way. In
particular Diffie–Hellman key exchange uses
finite cyclic groups. So the term group-
based cryptography refers mostly to
cryptographic protocols that use infinite
nonabelian groups such as a braid group.
7

8. USE OF Diffie–Hellman key exchange
✘ IT USES CYCLIC SUBGROUP OF FINITE GROUPS.
✘ THE APPROACH IS TO SEARCH FOR EXAMPLES
WHICH CAN BE REPRESENTED AND
MANIPULATED.
✘ ALTHOUGH IT IS USEFUL BUT IT IS NOT WIDELY
USED IN DAILY APPLICATIONS,INSTEAD
HASH(CRYPTOGRAPHY) AND NUMBERS IN
CRYPTOGRAPHY ARE USED.
8

9. ADVANTAGES OF USING
GROUPS IN
CRYPTOGRAPHY
✘ GROUPS ARE
REVERSIBLE
✘ EASY TO ENCRYPT THE
DATA
✘ EASY IN FINITE CYCLIC
PROBLEMS
DIS-ADVANTAGES OF
USING GROUPS IN
CRYPTOGRAPHY
✘ LESS ACCURACY
✘ TIME CONSUMING
✘ KEY(DEFFIE –
HELLMAN) FAILS AT
SOME POINTS
9

10. REAL WORLD EXAMPLE OF GROUP IN
CRYPTOGRAPHY
10
❌(ERROR)
UPPER FACE
A ATM CARD (2 FACE
AND 4 WAYS )
LOWER FACE
(THIS WILL
FAIL DUE TO
NO CHIP
DETECTION)
❌(ERROR)
❌(ERROR)

11. References
✘ http://ijariie.com/AdminUploadPdf/USE_OF_GROUP_THEORY_I
N_CRYPTOGRAPHY_ijariie5674.pdf
✘ https://www.researchgate.net/publication/323335090_Proble
ms_in_group_theory_motivated_by_cryptography
✘ https://en.wikipedia.org/wiki/Group-based_cryptography
11

12. 12