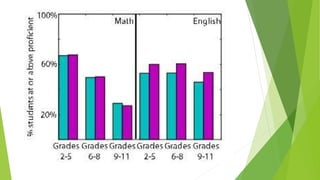
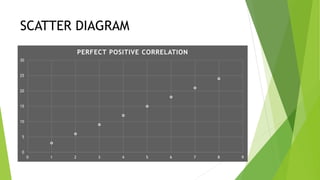
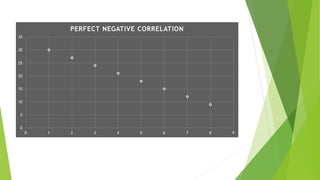
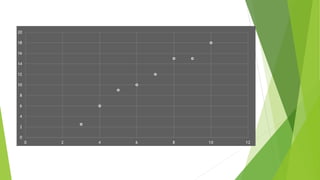
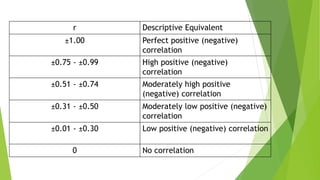
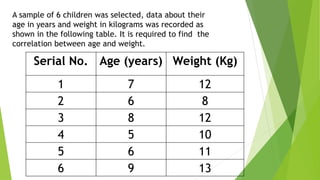
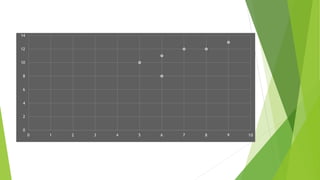
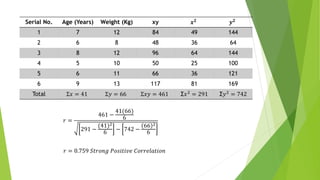
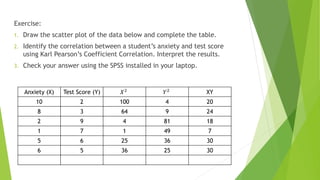
This document discusses correlation, a statistical technique used to determine the relationship between two variables. It defines positive correlation as a direct relationship where both variables increase or decrease together. Negative correlation is an inverse relationship where one variable increases as the other decreases. The Karl Pearson correlation coefficient formula is provided to calculate correlation between -1 and 1, with values closer to 1 or -1 indicating a stronger correlation. An example applies the formula to calculate a strong positive correlation between age and weight using sample child data.

4. PRICE

5. SPEED TIME

6. CORRELATION
is a statistical technique used to
determine the degree to which two
variables are related.

7. POSITIVE CORRELATION
 implies a direct relationship between the
variables, that is, as one increases (or decreases),
the other also increases (or decreases).
NEGATIVE CORRELATION
 implies an inverse relationship such that as one
variable increases, the other decreases.

8. PRICE

9. SCATTER DIAGRAM
0
5
10
15
20
25
30
0 1 2 3 4 5 6 7 8 9
PERFECT POSITIVE CORRELATION

10. 0
5
10
15
20
25
30
35
0 1 2 3 4 5 6 7 8 9
PERFECT NEGATIVE CORRELATION

11. 0
2
4
6
8
10
12
14
16
18
20
0 2 4 6 8 10 12

12. KARL PEARSON’S CORRELATION
COEFFICIENT FORMULA
WHERE: X = first variable under study
Y = second variable under study
n = total number of pairs



















  
  
n
y)(
y.
n
x)(
x
n
yx
xy
r
2
2
2
2

13. r Descriptive Equivalent
±1.00 Perfect positive (negative)
correlation
±0.75 - ±0.99 High positive (negative)
correlation
±0.51 - ±0.74 Moderately high positive
(negative) correlation
±0.31 - ±0.50 Moderately low positive (negative)
correlation
±0.01 - ±0.30 Low positive (negative) correlation
0 No correlation

14. Serial No. Age (years) Weight (Kg)
1 7 12
2 6 8
3 8 12
4 5 10
5 6 11
6 9 13
A sample of 6 children was selected, data about their
age in years and weight in kilograms was recorded as
shown in the following table. It is required to find the
correlation between age and weight.

15. 0
2
4
6
8
10
12
14
0 1 2 3 4 5 6 7 8 9 10

16. Serial No. Age (Years) Weight (Kg) xy 𝒙 𝟐
𝒚 𝟐
1 7 12 84 49 144
2 6 8 48 36 64
3 8 12 96 64 144
4 5 10 50 25 100
5 6 11 66 36 121
6 9 13 117 81 169
Total Σ𝑥 = 41 Σ𝑦 = 66 Σ𝑥𝑦 = 461 Σ𝑥2
= 291 Σ𝑦2
= 742
𝑟 =
461 −
41(66)
6
291 −
(41)2
6
− 742 −
66 2
6
𝑟 = 0.759 𝑆𝑡𝑟𝑜𝑛𝑔 𝑃𝑜𝑠𝑖𝑡𝑖𝑣𝑒 𝐶𝑜𝑟𝑟𝑒𝑙𝑎𝑡𝑖𝑜𝑛

17. Exercise:
1. Draw the scatter plot of the data below and complete the table.
2. Identify the correlation between a student’s anxiety and test score
using Karl Pearson’s Coefficient Correlation. Interpret the results.
3. Check your answer using the SPSS installed in your laptop.
Anxiety (X) Test Score (Y) 𝑋2
𝑌2
XY
10 2 100 4 20
8 3 64 9 24
2 9 4 81 18
1 7 1 49 7
5 6 25 36 30
6 5 36 25 30

18. Generalization
 Correlation – is a statistical technique used to determine the degree
to which two variables are related.
 Positive Correlation – if the values of two variables changing with the
same direction
 Negative Correlation – when the values of variables change with
opposite direction.
Two Methods for Identifying the Relationship between Two Variables
 Scatter Diagram
 Karl Pearson’s Correlation Coefficient Formula