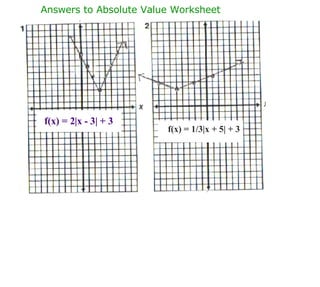
The document covers solving absolute value equations and inequalities, detailing the necessary steps and examples for both. It explains the properties of absolute values, including how to isolate them and solve related equations or inequalities graphically. The material includes specific problem sets and solution strategies for various cases, emphasizing understanding and checking solutions.

1. For those of you who missed it... Absolute Value!!!

2. 1. 2. 3. 4. 5. 6. Domain: (- ∞ , ∞ ) Range: [2, ∞ ) Domain: (- ∞ , ∞ ) Range: (- ∞, -2] Domain: (- ∞ , ∞ ) Range: [-1, ∞ ) Domain: (- ∞ , ∞ ) Range: [-2, ∞ ) Domain: (- ∞ , ∞ ) Range: (- ∞, 3] Domain: (- ∞ , ∞ ) Range: (- ∞, 1 ] Answers to Absolute Value Worksheet

3. Answers to Absolute Value Worksheet f(x) = 2|x - 3| + 3 f(x) = 1/3|x + 5| + 3

4. Answers to Absolute Value Worksheet f(x) = -3/2|x - 5| - 4 f(x) = -3/2|x + 6| - 2

5. Answers to Absolute Value Worksheet f(x) = 3|x - 4| - 10 f(x) = -2|x - 4| + 9

6. Answers to Absolute Value Worksheet f(x) = 4|x + 5| + 9 f(x) = 3/5|x + 4| - 8

7. 2x + 3 = 6 2x + 3 = -6 2x = 3 2x = -9 x = 3/2 x = -9/2 Solving Absolute Value Equations... Absolute Value: For any real number x, |x| = { -x, if x < 0 0, if x = 0 x, if x > 0 Recall: When solving equations, isolate the absolute value. Here are a few examples... 1. 5|2x + 3| = 30 |2x + 3| = 6 Don't forget to check!!! 5|6| = 30  5|-6| = 30  solution set: {3/2, -9/2}

8. example 2: -2|x + 2| + 12 = 0 -2|x + 2| = -12 |x + 2| = 6 isolate the absolute value! x + 2 = -6 x = -8 x + 2 = 6 x = 4 -2|-6| + 12 = 0 -2|6| + 12 = 0 {4, -8}

9. 5|3×+ 7|=-65 |3x + 7|=-13 absolute value cannot be negative!! example 3: {}

10. {3} example 4: |2x + 12| = 7x - 3 2x + 12 = 7x - 3 2x + 15 = 7x 15 = 5x 3 = x 2x + 12 = -(7x - 3) 2x + 12 = -7x + 3 9x + 12 = 3 9x = -9 x = -1 |18| = 18 |10| = -10 reject!

11. Absolute Value Inequalities Recall: |ax+b|=c, where c>0 ax+b=c ax+b=-c |ax+b|<c think: between &quot;and&quot; -c < ax+b < c ax+b < c and ax+b > -c ax+b>c or ax+b<-c why? we will express < or ≤ as an equivalent conjunction using the word AND |ax+b|>c think: beyond &quot;or&quot; we will express > or ≥ as an equivalent disjunction using the word OR

12. I. Less than... a) |x| < 5 x < 5 and x >-5 written as solution set: {x: -5< x < 5} Graph on a number line! use open circles! shade between!!! 1 0 2 3 4 5 6 7 8 9 10 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10

13. b) |2x - 1| < 11 2x-1<11 and 2x-1>-11 2x < 12 and 2x > -10 x < 6 and x > -5 {x: -5 < x < 6} 1 0 2 3 4 5 6 7 8 9 10 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10

14. c) 4|2x + 3| - 11 ≤ 5 4|2x + 3| ≤ 16 |2x + 3| ≤ 4 2x + 3 ≤ 4 AND 2x + 3 ≥ -4 2x ≤ 1 AND 2x ≥ -7 x ≤ 1/2 AND x ≥ -7/2 notice closed ends! -1 0 -2 -3 -4 -5 1 2 3 4 5

15. d) |7x + 10| < 0 think.... can an absolute value be negative??? NO!! {}

16. II. Greater than... a) |x| > 5 x > 5 or x < -5 written as solution set: {x: x > 5 or x < -5} I nterval notation (we will not use this, just set, but as an FYI): (- ∞ , -5) ∪ (5, ∞ ) Graph on a number line! use open circles! shade beyond!!! 1 0 2 3 4 5 6 7 8 9 10 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10

17. b) |2x - 1| > 11 2x-1>11 or 2x-1<-11 2x > 12 or 2x < -10 x > 6 or x < -5 {x: x > 6 or x < -5} 1 0 2 3 4 5 6 7 8 9 10 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10

18. c) 4|2x + 3| - 11 ≥ 5 4|2x + 3| ≥ 16 |2x + 3| ≥ 4 2x + 3 ≥ 4 OR 2x + 3 ≤ -4 2x ≥ 1 OR 2x ≤ -7 x ≥ 1/2 OR x ≤ -7/2 notice closed ends! -1 0 -2 -3 -4 -5 1 2 3 4 5

19. d) |7x + 10| > 0 think.... when is an absolute value greater than 0??? always!! {x: x ∈ R } x is a real number! -1 0 -2 -3 -4 -5 1 2 3 4 5

20. LAST ONE! 5 < |x + 3| ≤ 7 |x + 3| >5 |x + 3| ≤ 7 x + 3 > 5 or x + 3 < -5 x+ 3 ≤ 7 and x + 3 ≥ -7 x > 2 or x < -8 x ≤ 4 and x ≥ -10 now graph it! graph above the number line and look for the overlap. This is where your solution will appear. {x: -10 ≤ x < 8 or 2 < x ≤ 4} 1 0 2 3 4 5 6 7 8 9 10 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10

21. Remember to see me, email me or ask on the wiki if you have questions!! -Ms. P