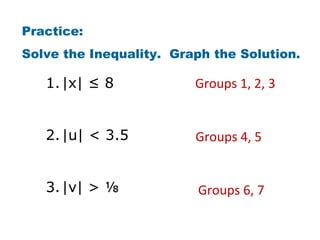
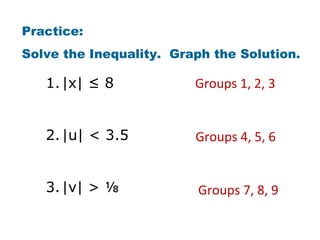
The document discusses how to solve absolute value inequalities by determining if the distance between a variable and 0 is less than, greater than, or equal to a given value, and representing the solutions on a number line. Examples are provided to illustrate solving inequalities such as |x| < 3, |x| > 3, and |x| ≥ 6, explaining that the solutions lie between, beyond, or beyond and equal to certain values. Practice problems are then given for students to solve additional absolute value inequalities and graph the solutions.

1. Unit 4.6
Solve Absolute Value Inequalities
Before you solved absolute
equations.
Now you will solve absolute value
inequalities.

2. Example: Using a Number Line
Recall that |x| = 3 means that the
distance between x and 0 is 3.
3
–3
–6 –5 –4 –3 –2 –1 0 1 2 3 4 5
The solutions to the inequality
equation |x| = 3 are 3 and –3.

3. Example: Absolute Value Inequalities
The inequality |x| < 3 means that the
distance between x and 0 is less than 3.
Let’s use the word between to describe
the value inequalities.
-3 < x < 3
–6 –5 –4 –3 –2 –1 0 1 2 3 4 5
Graph of |x| < 3

4. Example: Absolute Value Inequalities
The inequality |x| > 3 means that the
distance between x and 0 is greater than 3.
Let’s use the word beyond to describe the
value inequalities.
x < -3 or x > 3
–6 –5 –4 –3 –2 –1 0 1 2 3 4 5
Graph of |x| > 3

5. Example:
Solve the Inequality |x| ≥ 6 and graph your
solution.
The distance between x and 0 is greater
than or equal 6. So, x ≤ -6 or x ≥ 6.
Let’s use the word beyond to describe the
value inequalities.
–9 –6 –3 0 3 6
Graph of |x| ≥ 6

6. Example:
Solve the Inequality |x| ≤ 0.5 and graph
your solution.
The distance between x and 0 is less than
or equal to 0.5. So, -0.5 ≤ x ≤ 0.5.
Let’s use the word between to describe
the value inequalities.
–1 –0.5 0 0.5
Graph of |x| ≤ 0.5

7. Practice:
Solve the Inequality. Graph the Solution.
1. |x| ≤ 8 Groups 1, 2, 3
2. |u| < 3.5 Groups 4, 5
3. |v| > ⅛ Groups 6, 7

8. Practice:
Solve the Inequality. Graph the Solution.
1. |x| ≤ 8 Groups 1, 2, 3
2. |u| < 3.5 Groups 4, 5, 6
3. |v| > ⅛ Groups 7, 8, 9

9. Start on your homework for tonight:
Textbook Page 229, # 3 - 8